乙烯热力学相平衡模型及相图研究

蒋斯麒，孙丽丽，李进锋，苏 洪，张军志，刘 罡

（中国石化 工程建设有限公司，北京 100021）

乙烯是应用最为广泛的石化原料和产品之一。随着工程技术及材料性能的提高，在乙烯的工业生产及储运领域［1-2］以及新型聚乙烯材料的研发及制造领域［3-6］，乙烯所处温度及压力等条件都日趋苛刻。例如，高压法聚乙烯工艺的反应压力高达180～350 MPa［7-8］，反应温度为300 ℃；乙烯装置的低温压缩机组操作温度低至-115 ℃，导致乙烯在低温区域的相行为严重影响了装置的安全运行［9］。

国内缺乏对乙烯热力学相平衡模型及相图的研究。在乙烯工业及工程设计领域，尽管Aspen Plus 等过程模拟软件应用较早［10］，但缺乏乙烯的固-液两相相平衡计算模型，工程技术人员难以获取乙烯的热力学相图。因此，系统开展乙烯的相平衡热力学研究，精确绘制乙烯热力学相图，对乙烯相关新工艺技术与设备研发具有重要意义。

本工作在研究了大量乙烯相平衡热力学实验数据的基础上，评价及定量描述了实验数据，给出了乙烯的固Ⅰ-固Ⅱ-液、气-固-液两个三相点与临界点的推荐值；优化了部分乙烯热力学相平衡模型，即通过使用推荐值并采用非线性方程的参数拟合及回归的方法，提出了乙烯的热力学相平衡模型（冷凝曲线、熔融曲线Ⅰ、熔融曲线Ⅱ、熔融曲线Ⅰ+Ⅱ、升华曲线），并绘制了乙烯的热力学相图。

1 乙烯相平衡点

1.1 气–固–液和固Ⅰ–固Ⅱ–液两个三相点

乙烯存在两个三相点，即常规的气-固-液三相点和固Ⅰ-固Ⅱ-液三相点。乙烯气-固-液三相点的实验数据［11-17］见表1。本工作推荐使用文献［16］的气-固-液三相点温度103.986 K、三相点压力122.52Pa。

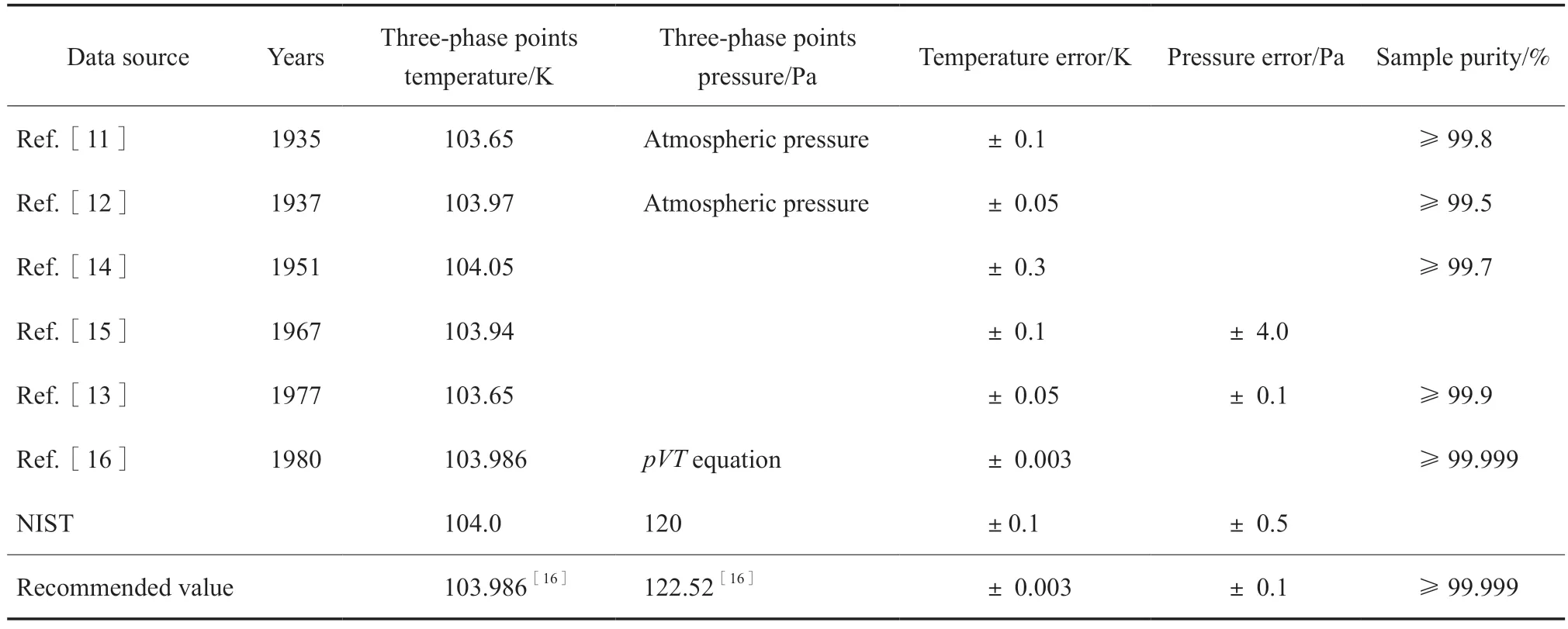
表1 乙烯气-固-液三相点的实验数据［11-17］Table 1 Experimental results of the gas-solid-liquid triple point of ethylene［11-17］

乙烯的固Ⅰ-固Ⅱ-液三相点首次由Ligthart等［18］测定，他们通过NMR 方法，在超低温度（77 K）和超高压力（250 MPa）的极其苛刻的实验条件下，对固态乙烯熔融过程进行了研究。研究结果表明，在一定压力下，由纯乙烯形成的固相Ⅰ在熔融过程中，因温度逐渐升高，内部的晶体结构随之变化［19-20］，从而形成塑性晶体的新固相Ⅱ；继续升高温度，固态乙烯最终熔融成为液态，所以固相Ⅱ为固态乙烯由固相Ⅰ熔融形成液态乙烯的过渡相态。上述实验结果证明，乙烯在较高压力下存在固Ⅰ-固Ⅱ-液共存的三相点。Ligthart 等［18］测定的该三相点温度为（110.36±0.1）K、三相点压力为46.80 MPa。美国国家标准与技术研究院（NIST）数据库没有列出该三相点的温度和压力。

1.2 临界点

受试样纯度和实验设备的限制，乙烯临界点的早期实验数据［17，21-22］仅供参考。乙烯临界点的实验数据［23-28］见表2。本工作推荐使用文献［24］的乙烯临界点温度282.344 K 和由对应温度下的pVT热力学模型外推计算得到的临界点压力5.041 3 MPa［25］。

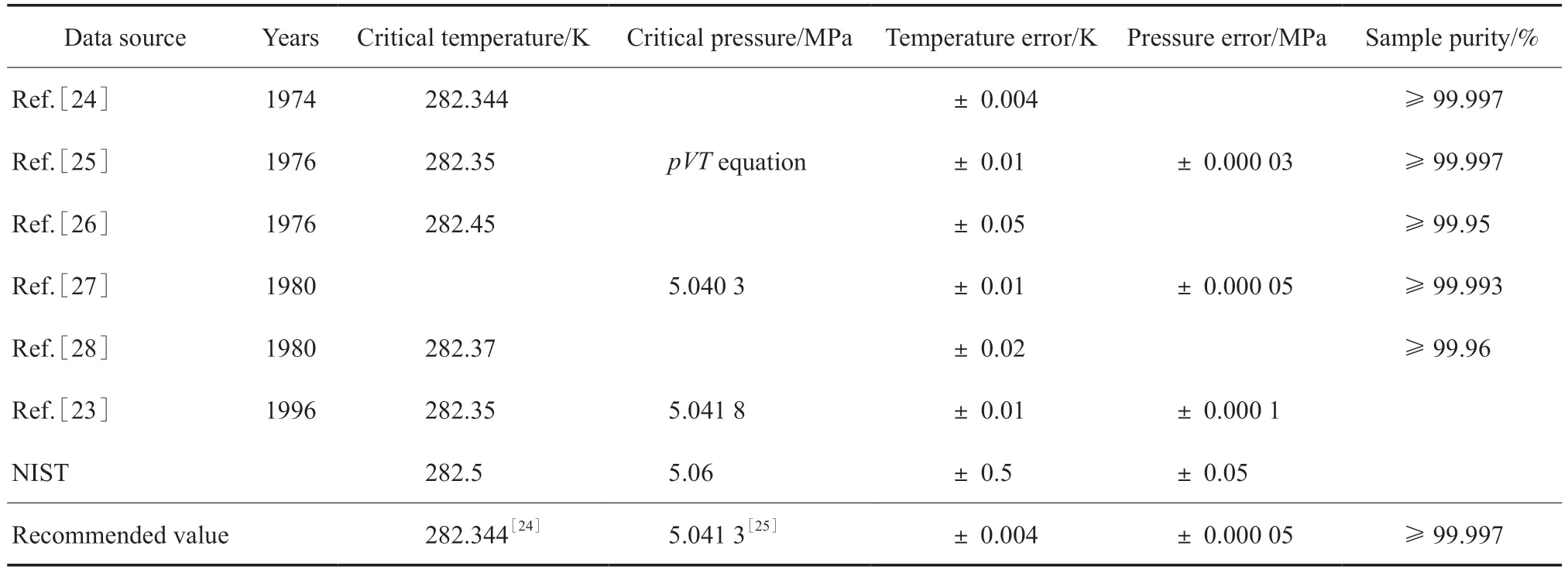
表2 乙烯临界点的实验数据［23-28］Table 2 Experimental results of the critical point of ethylene［23-28］

2 乙烯的相平衡热力学实验数据及模型

2.1 冷凝曲线

Micheles 等［29］早在1950 年建立了乙烯饱和蒸气压的热力学方程（式（1）），但该方程在临界温度附近的拟合误差较大。

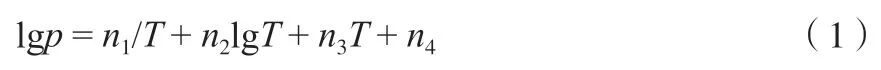
采用Plank-Riedel 方程（式（2））也可计算乙烯的饱和蒸气压：

式中，pr=p/pt，Tr=T/Tt；p为乙烯在温度T的饱和蒸气压，MPa；pt和Tt分别为乙烯的气-固-液三相点压力122.52 Pa 和三相点温度103.986 K；ni（i=1～3）为方程参数。方程（2）对氮气、氧气和氢气等气体的气–液相平衡数据的拟合效果良好［30］。方程（2）中的ni（i=1～3）均为经验常数，由相平衡实验数据拟合得到。由于乙烯气体的结构比上述气体复杂，且存在分子内运动，将方程（2）修改为增加拟合参数n4的方程（3）：

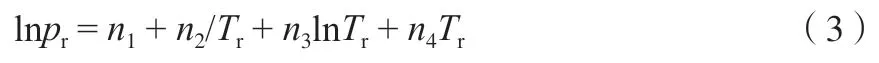
Jacobsen 等［21］提出了与临界温度和压力关联的相平衡模型：

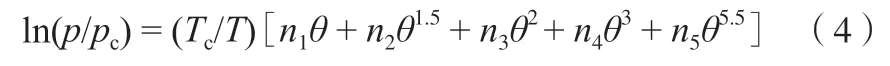
式中，θ=1-T/Tc；pc和Tc分别为乙烯的临界压力5.041 3 MPa 和临界温度282.344 K。

分别用方程（3）和方程（4）对乙烯的冷凝曲线进行拟合，拟合相对误差∆δ用式（5）计算：

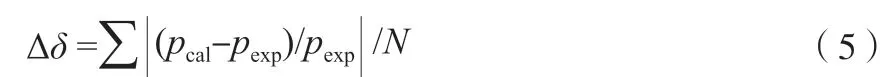
式中，N是实验值数量；pcal和pexp分别为饱和蒸气压的计算值和实验值，MPa。采用文献［16］和文献［13］的乙烯饱和蒸气压实验数据，由方程（3）和方程（4）拟合得到了乙烯的冷凝曲线，拟合结果如表3 和图1 所示。由表3 可见，方程（3）和方程（4）在103.986～282.344 K 区间内的∆δ分别为0.086 7%和0.679 3%，拟合效果明显优于Micheles 等［29］的经验模型；另外，方程（3）的拟合参数比方程（4）少，但拟合效果明显优于方程（4）。图1b 对比了方程（3）和方程（4）的拟合结果，方程（3）显著优于方程（4）。

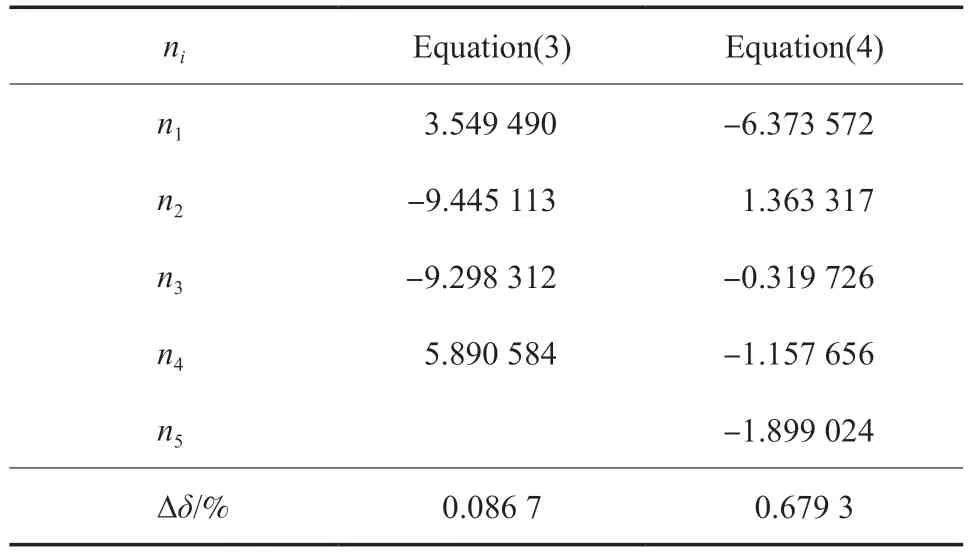
表3 饱和蒸气压方程（3）和方程（4）的参数拟合值Table 3 Numerical values of coefficients(ni) of the saturated vapor pressure equation(3) and equation(4)

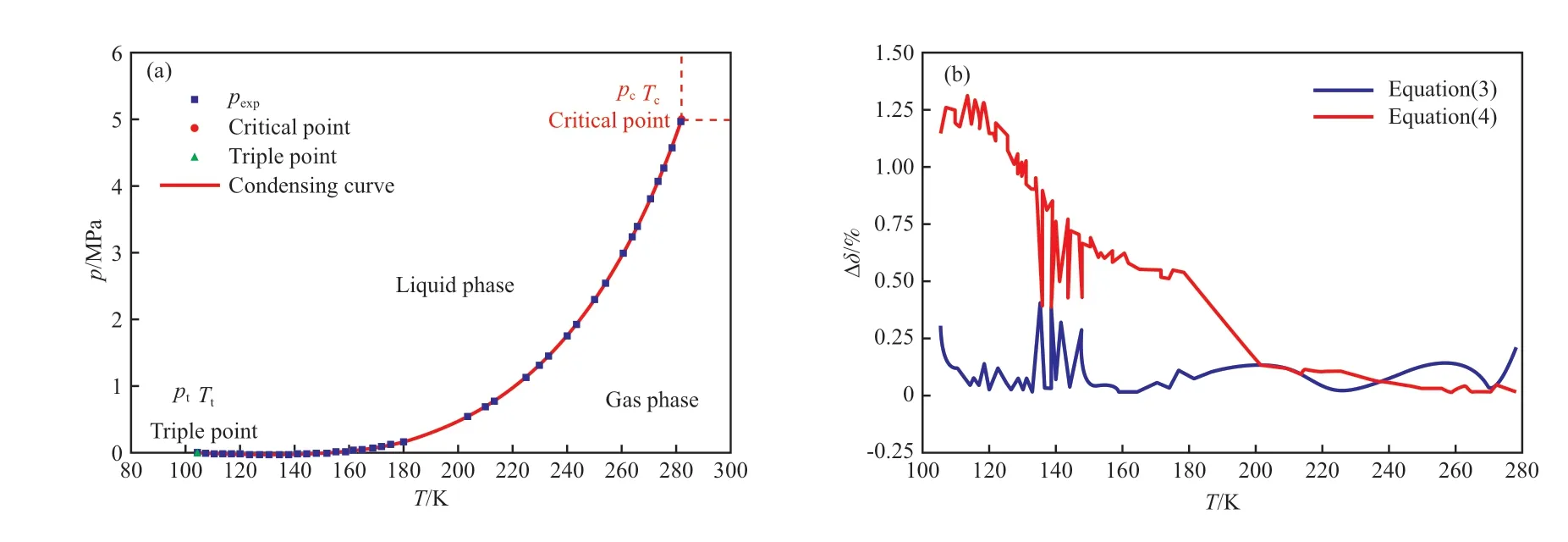
图1 乙烯的饱和蒸气压拟合数据及拟合方程的比较Fig.1 Comparison of saturated vapor pressure fitting data and fitting equations of ethylene.

2.2 熔融曲线

乙烯熔融曲线的实验条件极其苛刻，温度低至104.216 K，压力为36 MPa，所以数据相对较少［16，18，31］。Straty［16］测定了乙烯常规的气-固-液三相点压力，并外推得到准确的三相点温度；同时，还测定了乙烯在低温环境中的熔融压力，将乙烯在低温环境中形成的固相称为固相Ⅰ。Straty［16］建立的乙烯熔融曲线Ⅰ的热力学方程为：

本工作在此基础上提出：

式中，pr=p/pt，Tr=T/Tt；pm为乙烯在温度T的熔融压力，MPa；pt和Tt分别为乙烯的气-固-液三相点压力122.52 Pa 和三相点温度103.986 K；ni（i=1～2）为方程参数。用方程（7）拟合了乙烯固相Ⅰ在熔融温度介于103.986～110.36 K 的熔融压力，结果见表4。从表4 可知，方程（7）的∆δ值为0.053%，拟合精度高于文献值［16］。

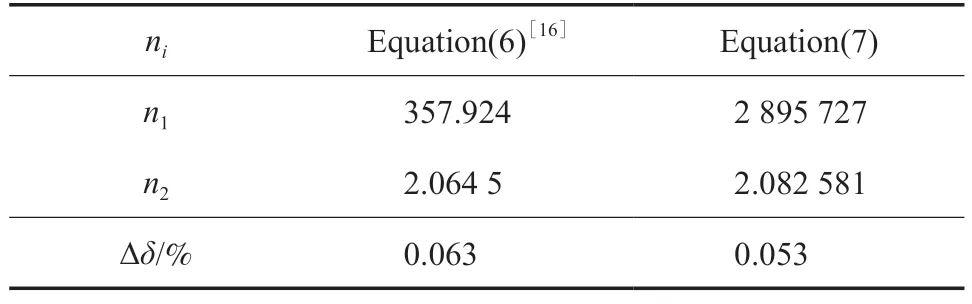
表4 熔融曲线Ⅰ的参数拟合值Table 4 Numerical values of ni of the melting curve Ⅰ

根据Ligthart 等［18］的实验结果，乙烯的第二个三相点温度为110.36 K，三相点压力为46.80 MPa。Ligthart 等［18］利用NMR 方法，在77～140 K、0～250 MPa 内对乙烯的相变过程进行了研究，揭示了固态乙烯在熔融过程中未知固相的形成机理。将乙烯在高温、高压环境中形成的新固相称为固相Ⅱ。NMR 研究结果表明，乙烯的固相Ⅱ是一种塑性晶体，呈立方体结构。固态乙烯由固相Ⅰ变为固相Ⅱ的熔融过程是由有序向无序转变的熵增过程。当乙烯熔融压力高于46.8 MPa 时，熔融过程如下：随着温度的升高，低温、高压固态乙烯（固相Ⅰ）的晶格结构逐渐变化，熔融形成固相Ⅱ；随着温度持续升高，固相Ⅱ的立方体晶格结构最终熔融形成液态乙烯。

针对熔融曲线Ⅱ和熔融曲线Ⅰ+Ⅱ，Ligthart等［18］提出了方程（8）：

本工作为熔融曲线Ⅱ和熔融曲线Ⅰ+Ⅱ提出的方程依然为方程（7），但pt和Tt分别为46.80 MPa 和110.36 K（即乙烯的第二个三相点压力和温度）。分别用方程（7）和方程（8）拟合了熔融曲线Ⅱ在熔融温度介于110.36～ 140.466 K 的熔融压力以及熔融曲线Ⅰ+Ⅱ在熔融温度介于110.36～130.29 K 的熔融压力，结果分别见表5和表6。由表5 可知，方程（7）和方程（8）对应熔融曲线Ⅱ的∆δ分别为0.020% 和0.040%；由表6 可知，方程（7）和方程（8）对应熔融曲线Ⅰ+Ⅱ的∆δ分别为 0.015% 和 0.033%。结果表明，方程（7）所需参数比改进的Ligthart 热力学模型［18］（方程（8））的参数少，但拟合精度提高了，且可应用于整个熔融过程。此外，将Tt值代入方程（7）和方程（8），通过方程（7）可以准确得到pt值，但通过方程（8）不能准确得到pt值，这是方程（7）的另一个优点。

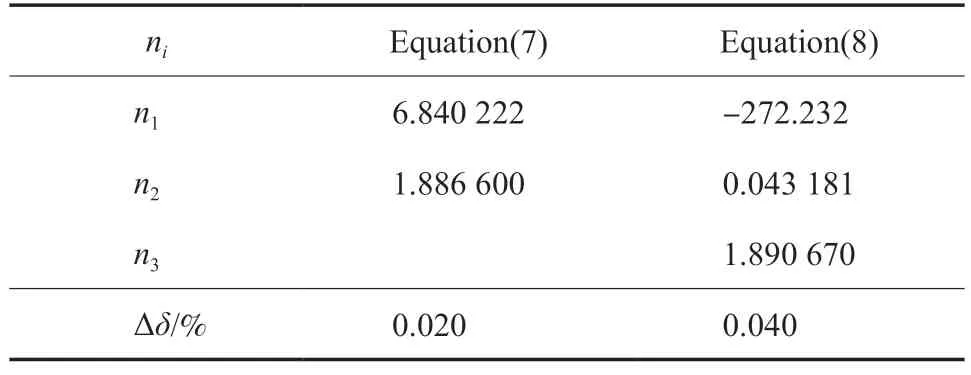
表5 熔融曲线Ⅱ的参数拟合值Table 5 Numerical values of ni of the melting curve Ⅱ

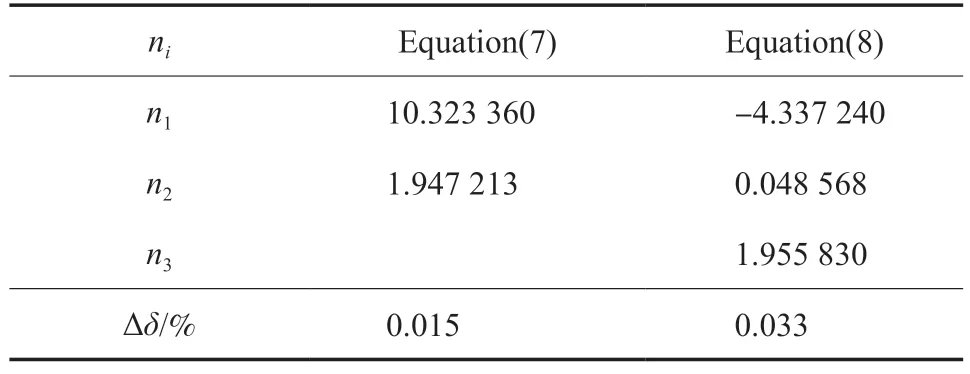
表6 熔融曲线Ⅰ+Ⅱ的参数拟合值Table 6 Numerical values of ni of the melting curve Ⅰ+Ⅱ

综上所述，乙烯的熔融过程存在固相Ⅰ、固相Ⅱ和液相三相相变过程，当熔融温度在103.986～110.36 K 时，固态乙烯从固相Ⅰ直接熔融至液相；当熔融温度大于等于 110.36 K 时，固态乙烯从固相Ⅰ先熔融形成固相Ⅱ的过渡态，随着温度持续升高，再熔融至液相。所以，乙烯存在熔融曲线Ⅰ、熔融曲线Ⅱ、熔融曲线Ⅰ+Ⅱ三条熔融曲线，三条熔融曲线相交于固相Ⅰ–固相Ⅱ–液相三相共存的三相点。通过文献［18］的纯乙烯熔融温度和熔融压力实验数据，由方程（7）拟合得到了乙烯的三条熔融曲线，如图2 所示。

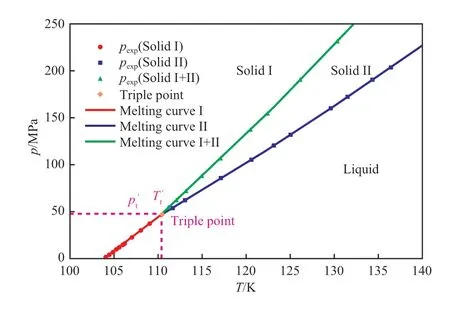
图2 乙烯熔融曲线的拟合数据与实验数据的对比Fig.2 Comparison of calculated and experimental values of melting curve of ethylene.

2.3 升华曲线

乙烯升华曲线的测定实验条件同样苛刻，实验数据少且珍贵。Bigeleisen 等［13］提出了乙烯升华过程的饱和蒸气压热力学方程：

式中，pt和Tt分别为三相点压力122.52 Pa 和三相点温度103.986 K；p为乙烯在温度T的升华压力（饱和蒸气压）。由于无论是升华过程还是冷凝过程均是气相与凝聚相的平衡过程，所以本工作依然通过方程（3）拟合乙烯的升华曲线。通过文献［13］的纯乙烯升华温度和饱和蒸气压实验数据，分别用方程（3）和方程（9）拟合了乙烯在92.3～103.986 K 区间内的升华压力，结果见表7 和图3。由表7 可知，方程（9）和方程（3）的∆δ分别为0.109 0%和0.092 8%，说明方程（3）的拟合精度更高。

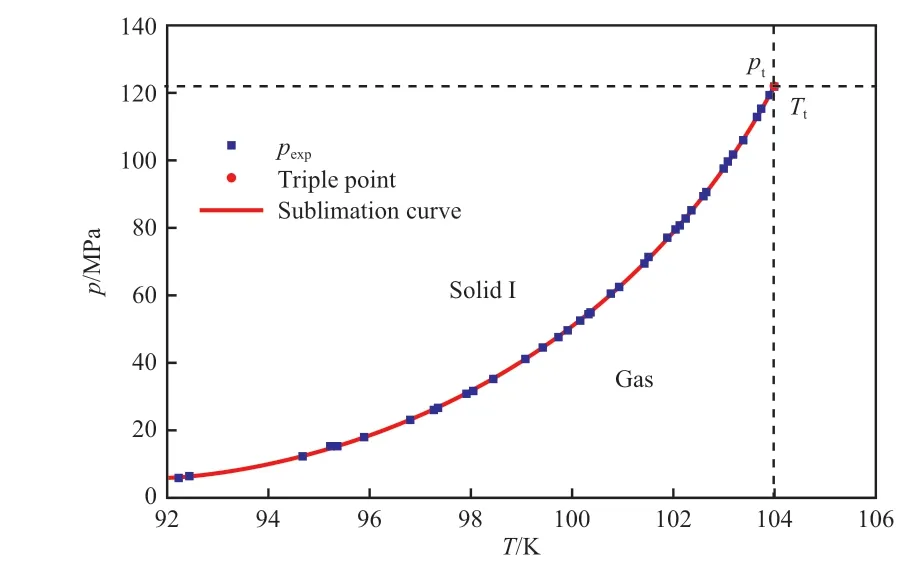
图3 乙烯升华曲线的拟合数据与实验数据的对比Fig.3 Comparison of calculated and experimental values of sublimation curve of ethylene.

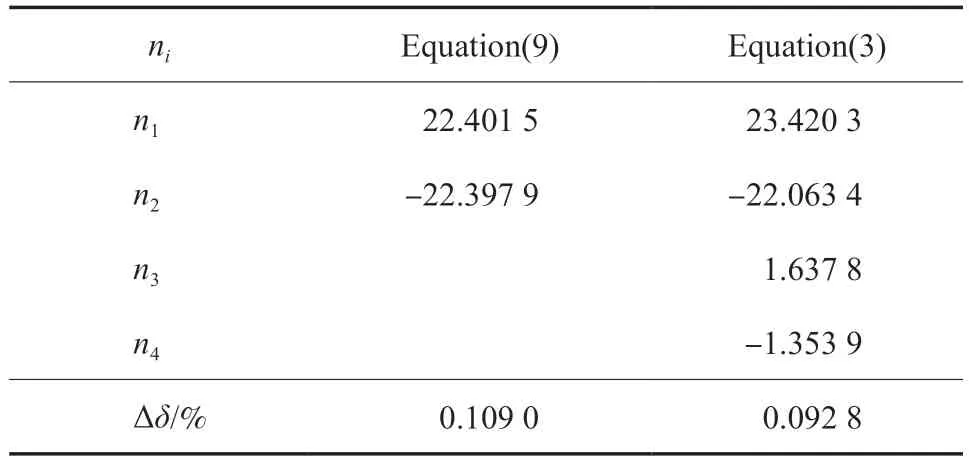
表7 升华曲线方程的参数拟合值Table 7 Comparison of the numerical values of ni of the sublimation curve equation

3 乙烯热力学相图

乙烯热力学相图的绘制对乙烯相关工艺及工程技术的设计与研发具有重要意义，是必不可少的热力学基础研究内容。在92.30～ 500.00 K、1×10–5～ 300 MPa 内绘制了乙烯的热力学相图，结果见图4。图4 中的乙烯热力学相图包含了三部分内容：第一部分为推荐的乙烯气-固-液三相点值及固Ⅰ-固Ⅱ-液三相点值；第二部分为乙烯临界点的推荐值；第三部分为本工作提出的乙烯相平衡热力学模型，即冷凝曲线和升华曲线采用方程（3），熔融曲线Ⅰ，Ⅱ，Ⅰ+Ⅱ采用方程（7）。上述方程对乙烯的冷凝曲线、熔融曲线和升华曲线的拟合结果见表8。图4 和表8 可为乙烯相关工艺、工程设计及研发提供纯乙烯的相平衡热力学实验数据和预测模型。

图4 乙烯的热力学相图Fig.4 Thermodynamics phase diagram of ethylene.

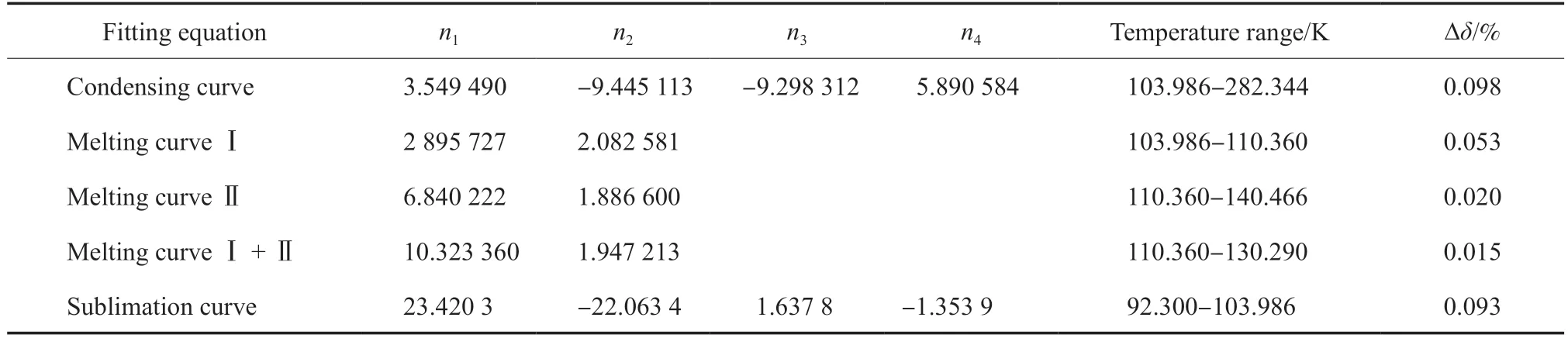
表8 乙烯相平衡热力学模型参数值的拟合结果汇总Table 8 Numerical values summary of ni for phase equilibrium equations of ethylene

4 乙烯在相平衡状态下的pVT 相图

乙烯在相平衡状态下的各相密度数据，即p-V与T-V相图，对乙烯相关工艺、工程设计及研发具有重要意义。但由于结晶态乙烯在工程领域应用极少，且相应基础热力学性质的实验测定难度极大，致使数据稀缺。因此，基于上述乙烯相平衡的研究，本工作采用乙烯的气-液、液-固相平衡状态的气相和液相数据，提出了p-V与T-V相图。

表9 列出了液-固相平衡状态下，基于熔融温度的乙烯液相密度实验值［25，32］，而表中不同熔融温度对应的熔融压力则由熔融曲线Ⅰ（方程（6））和熔融曲线Ⅱ（方程（6））计算获得。表10 列出了气-液相平衡状态下，基于冷凝压力的乙烯液相密度和气相密度实验值［32］，而表中不同冷凝压力对应的冷凝温度则由冷凝曲线（方程（3））计算获得。以表9 和表10 为基础，绘制了乙烯的p-V与T-V相图，结果见图5。

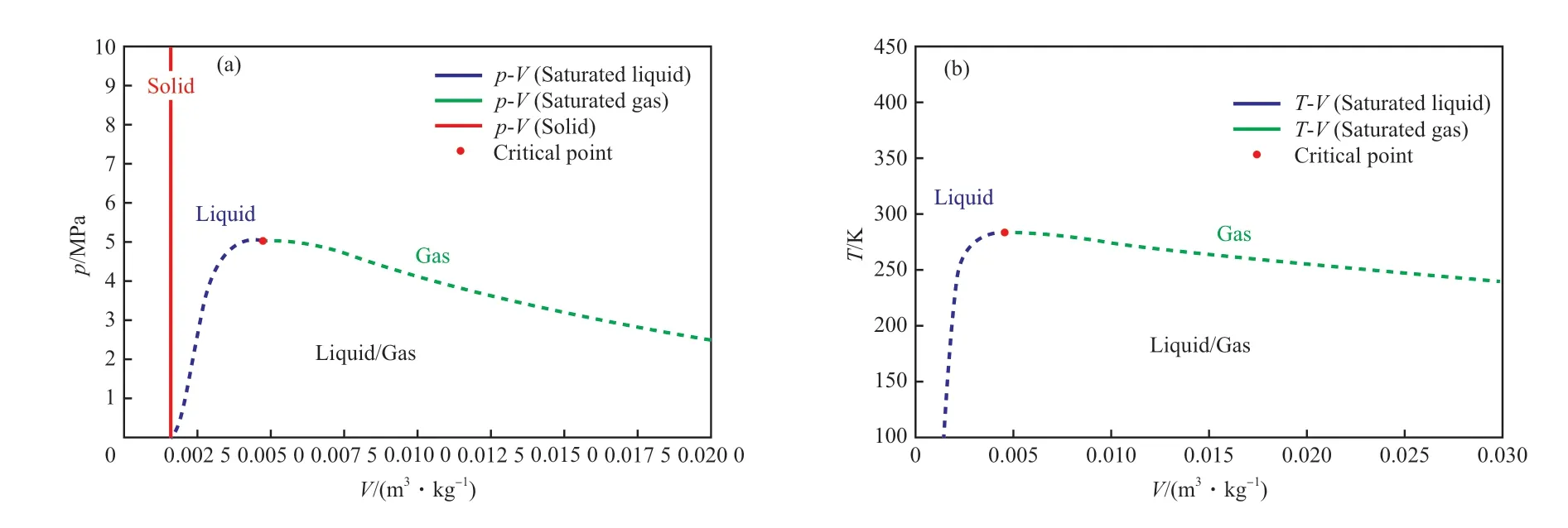
图5 乙烯在相平衡状态下的pVT 相图Fig.5 pVT phase diagram of ethylene in phase equilibrium.

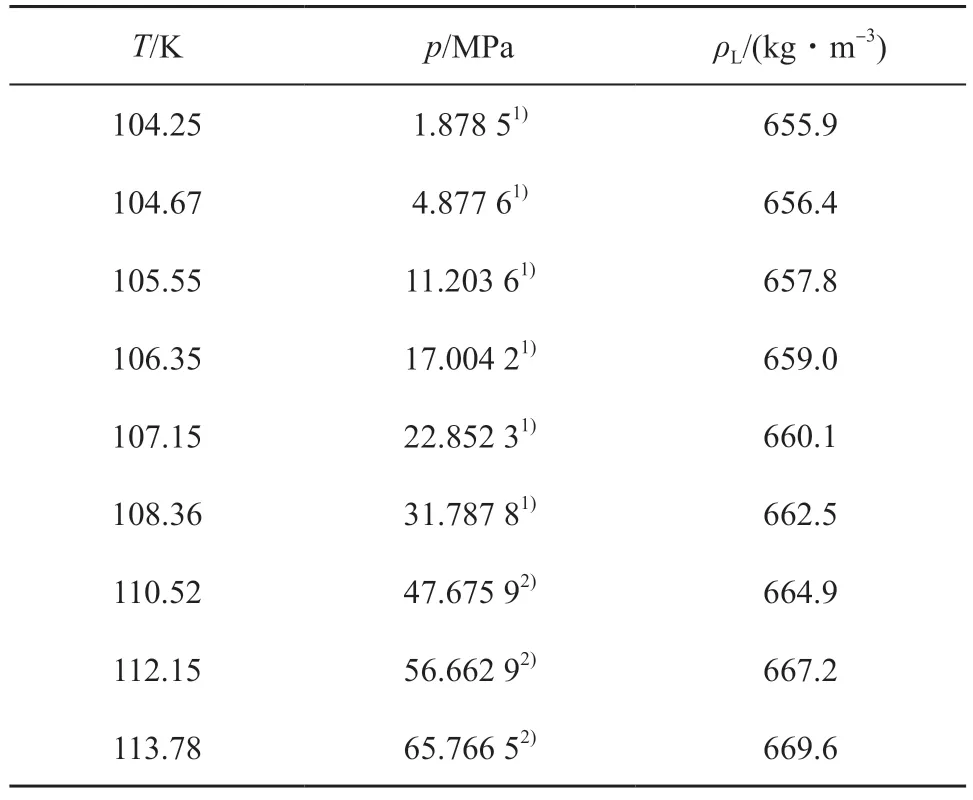
表9 液-固相平衡状态下的乙烯液相密度实验值［25，32］Table 9 Experiment data of liquid phase density(ρL) of ethylene in liquid-solid equilibrium［25，32］

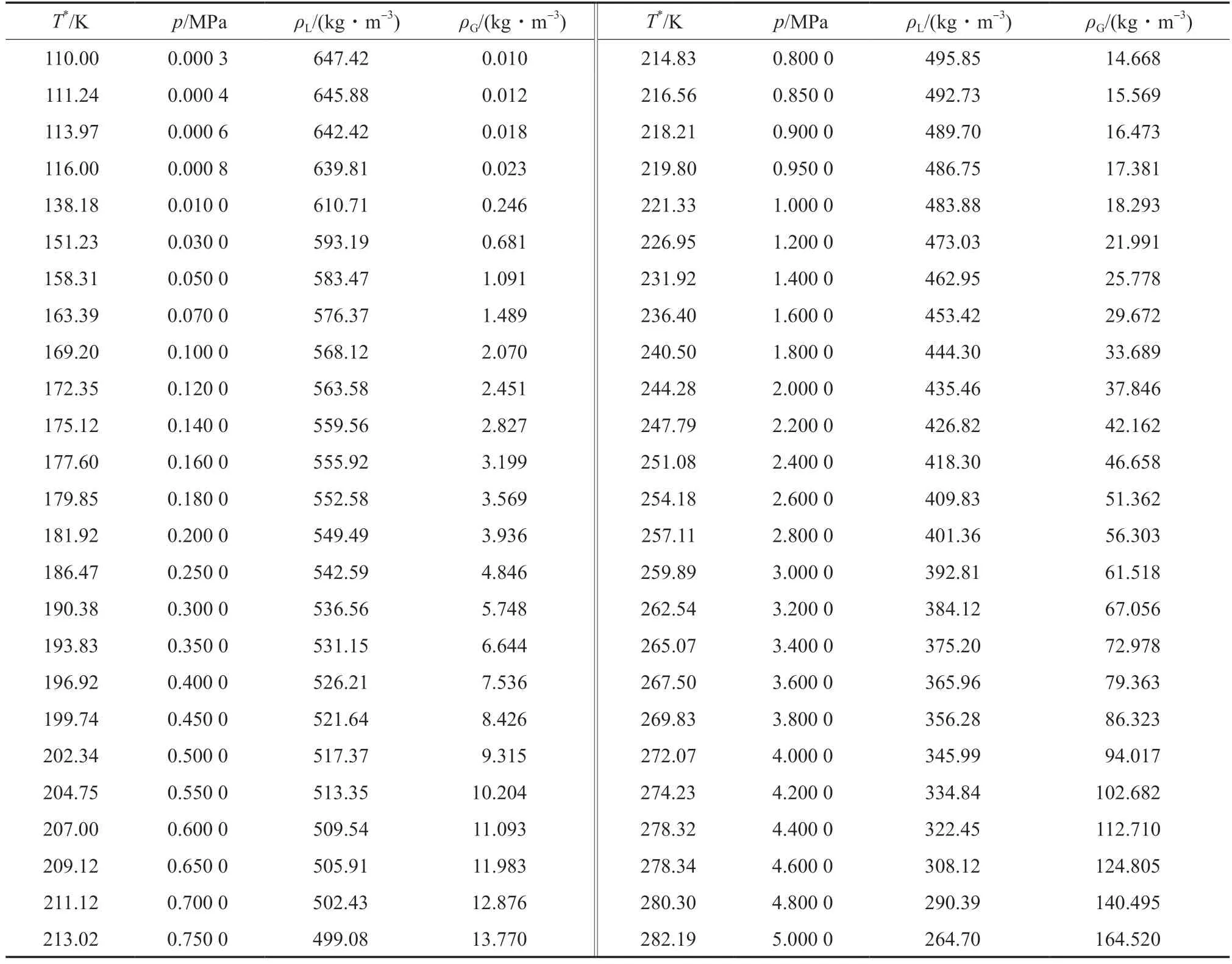
表10 气-液相平衡状态的乙烯液相密度和气相密度实验值［32］Table 10 Liquid phase density and gas phase density(ρG) of ethylene in gas-liquid phase equilibrium［32］

5 乙烯的汽化焓

乙烯的汽化焓常用于计算乙烯在气-液相变过程中的热量。乙烯在气-液相平衡状态下的气相焓和液相焓［32］及由冷凝曲线（方程（3））计算的相平衡温度下乙烯的汽化焓见表11。

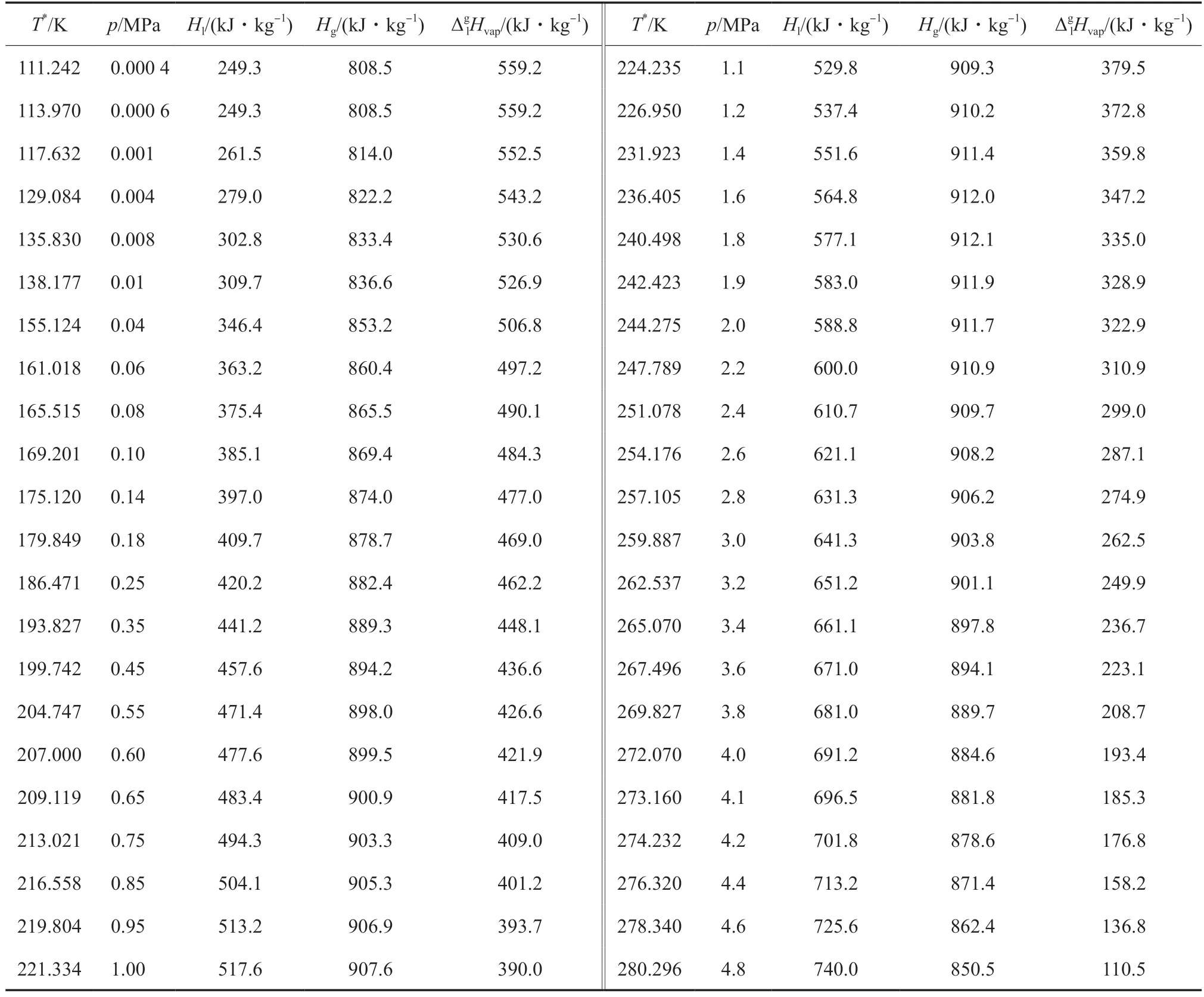
表11 气-液相平衡状态下的乙烯液相焓、气相焓和汽化焓Table 11 Liquid phase enthalpy(Hl)，gas phase enthalpy(Hg) and vaporization enthalpy(ΔglHvap) of ethylene in gas-liquid phase equilibrium

由于汽化焓是温度的函数，本工作以温度的多项式为基础，经相对误差分析确定了汽化焓的方程如下：

采用文献［32］的数据，用方程（10）拟合了乙烯气-液相平衡的汽化焓，拟合结果见表12 和图6。由表12 可知，方程（10）的拟合结果具有较高的准确度，Δδ为1.291%。

表12 汽化焓方程的参数拟合值Table 12 Numerical values of ni of vaporization enthalpy equation

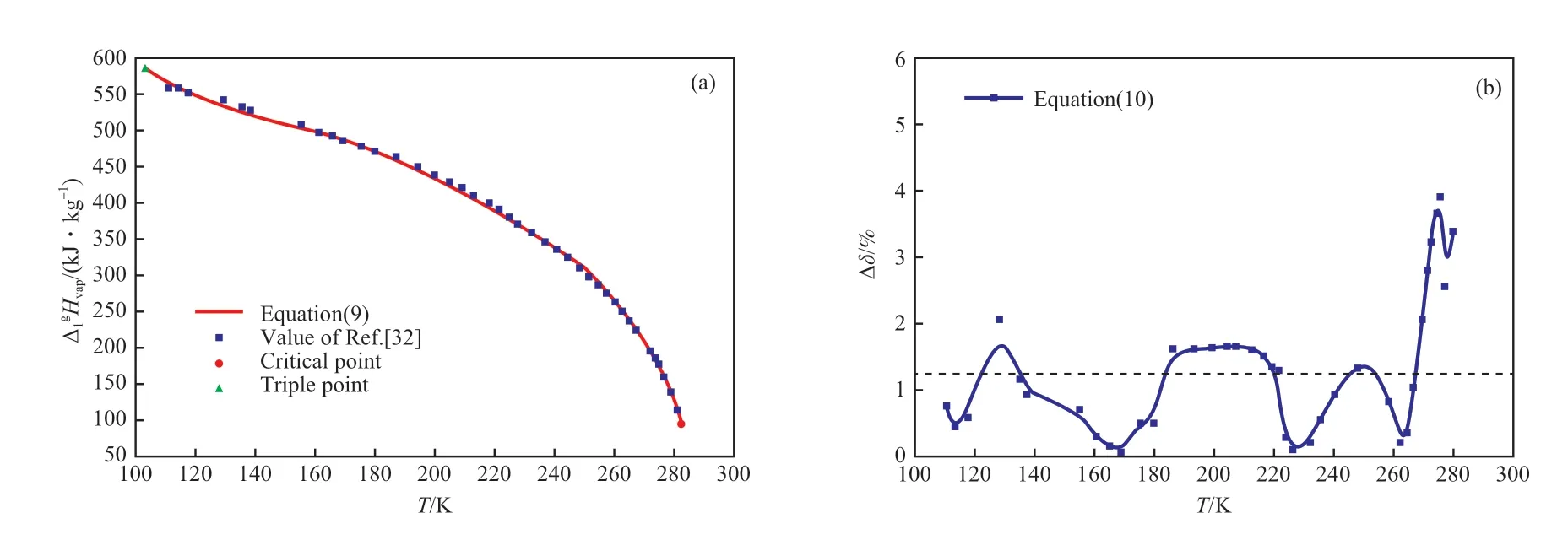
图6 乙烯的汽化焓拟合数据与文献数据的对比（a）及拟合结果（b）Fig.6 Comparison of fitting data with literature data of vaporization enthalpy of ethylene(a) and fitting results(b).

6 结论

1）研究了乙烯的热力学相平衡实验数据，乙烯气-固-液三相点的推荐值为温度103.986 K，压力122.52 Pa；固Ⅰ-固Ⅱ-液三相点的推荐值为温度110.36 K，压力46.80 MPa；临界点的推荐值为温度 282.344 K，压力5.041 3 MPa。

2）确定了乙烯的热力学相平衡方程，包括冷凝曲线、熔融曲线Ⅰ、熔融曲线Ⅱ、熔融曲线Ⅰ+Ⅱ及升华曲线方程，方程的拟合结果优于文献方程。

3）描述了温度区间92.30～500 K、压力区间1×10–5～300 MPa 内的乙烯相平衡行为，绘制了乙烯的热力学相图；根据乙烯的气-液、液-固相平衡状态的气相与液相数据，提出了乙烯的p-V和T-V相图。

4）建立了乙烯气-液相平衡的汽化焓方程，方程计算值的相对误差平均值为1.291%。

符号说明