在“说题”中成长

吕晓兰 王瑾

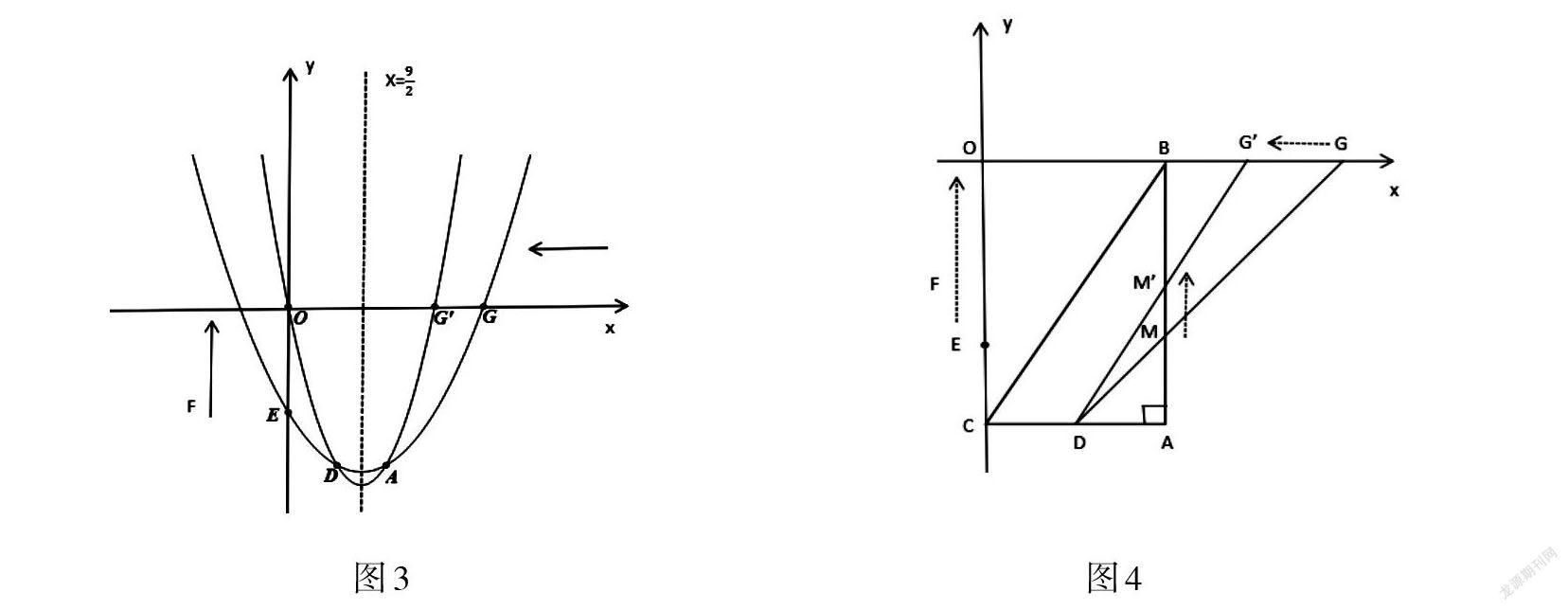
摘 要 数学说题作为一种研究数学解题的教研活动，有助于教师提升数学素养，促进专业发展。以二次函数综合题为例，具体呈现说题过程，剖析如何从解题方法、数学思想、题目变式，教学方法等方面进行对数学解题的深入研究。

关键词 数学说题 解题过程 回顾反思

教师的说题是一个将审题，分析解题思路、方法和回顾的思维过程按照一定的逻辑深入浅出的表达出来的过程。不同于教师解题，教师说题不仅仅是解题过程的呈现，还是在此基础上能够对题目进行科学理性的分析和理解。因此，教师对说题的研究不仅能够提升自身的教学技能及专业素养，更重要的是能够提高学生的解题能力，促进学生的数学思维发展。教师的说题内容大致包括命题意图、命题背景、教学与评价、题后反思等几个部分[1]。下面以沈阳中考模拟考试中一道二次函数压轴题为例进行“说题”。

一、原题呈现

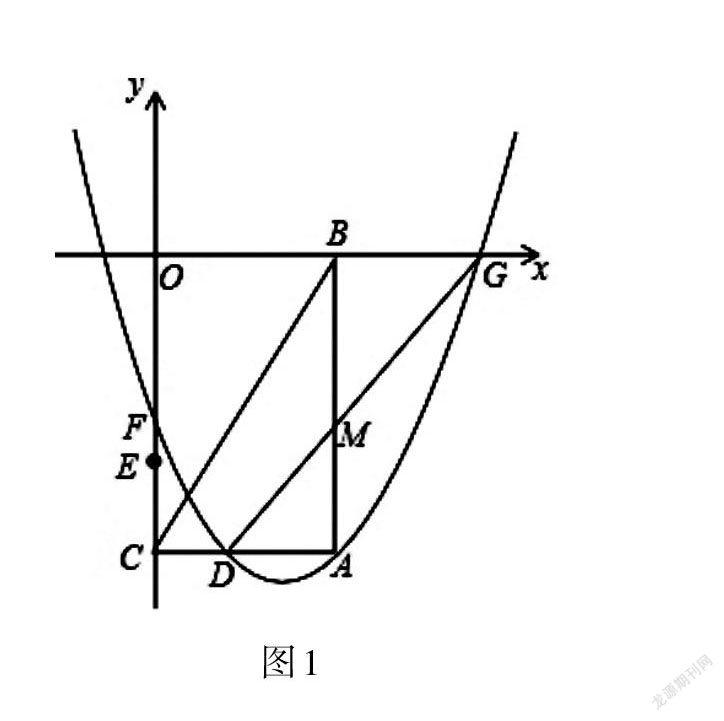
题目：如图1，在平面直角坐标系中，点A的坐标为（6，[-63]），AB⊥x轴于点B，AC⊥y轴于点C，连接BC。点D是线段AC的中点，点E的坐标为（0，[-43]），点F是线段EO上的一个动点。过点A、D、F的抛物线与x轴正半轴交于点G，连接DG交线段AB于点M。

（1）求∠ACB的度数;

（2）当点F运动到原点时，求过A、D、F三点的抛物线的函数表达式及点G的坐标;

（3）以线段DM为一边作等边三角形DMP，点P与点A在直线DG同侧，当点F从点E运动到点O时，请直接写出点P运动的路径的长。

二、命题背景分析

近几年来，各地中考数学压轴题多与二次函数有关，体现了多种数学思想方法的综合运用。其中，函数与动点结合的问题是考查的重难点。而有关动点轨迹、路径的问题一直都是关注的重点。此类问题涉及知识点较多，综合性较强，问题设置环环相扣，层层递进，巧妙融合多个数学知识的同时，又蕴含着丰富的数学思想方法，是提高学生数学核心素养的良好载体。

三、命题的立意分析

（一）数学知识技能方面

本题主要考查利用待定系数法求二次函数表达式，利用消元法或者代入法求解二元一次方程组;解直角三角形中的利用三角函数求角的度数，全等三角形的判定及性质，等边三角形的性质及图形旋转性质等内容。

（二）数学思想方法方面

本题中蕴含丰富的思想方法，主要包括化归、数形结合、几何直观、特殊化、由特殊到一般等重要的数学思想方法。

（三）数学学科核心素养方面

本题的解答需要学生能正确地识图、作图，注重考查学生的直观想象素养、数学运算和逻辑推理等素养。

四、解题过程及思路评析

（一）第一问

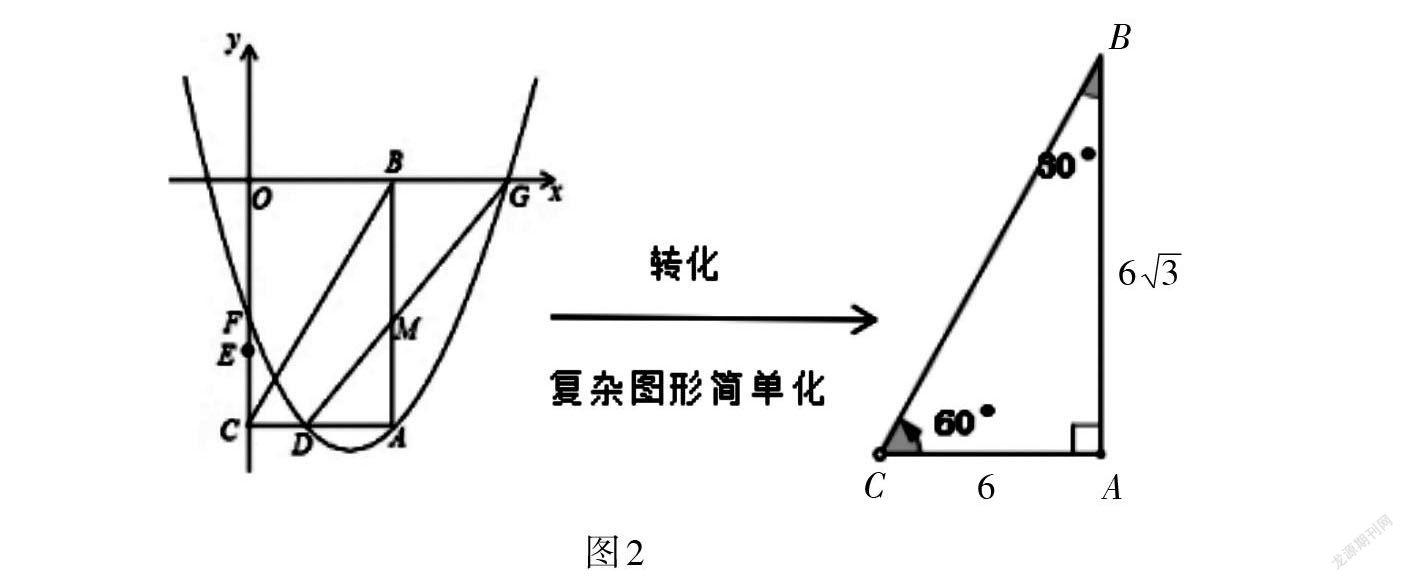
弄清问题，找出已知中的关键信息及隐含信息。本问首先明确是求角度数的问题，再结合已知条件不难发现，所求∠ACB处在直角三角形中，因此可以想到利用三角函数求角的度数，而且已知条件明确A点坐标（6，[-63]），由点的坐标确定线段的长，即可求出直角三角形两直角边，根据∠ACB的正切值求出角的度数，如图2。

【评析】本道题的解决主要利用三角函数求角的度数，运用数形结合的数学思想方法，从复杂的图形中提取简单基本图形，难度不大，计算简单，是对基础知识和技能的考查。

（二）第二问

关键信息：点F运动到原点，点D为线段AC中点，从关键信息中挖掘隐含条件即点F与点O重合。由点A坐标（6，[-63]）即可明确点D坐标为（3，[-63]）。因此，如图3可将求过A、D、F三点抛物线的表达式转化为求过A、D、O三点的抛物线。并且在三点的坐标已知的情况下，利用待定系数法设一般式即可求出。但在本问中，部分同学会发现A、D两点关于某直线对称，所以先求出对称轴，再利用设顶点式也可求出二次函数表达式。

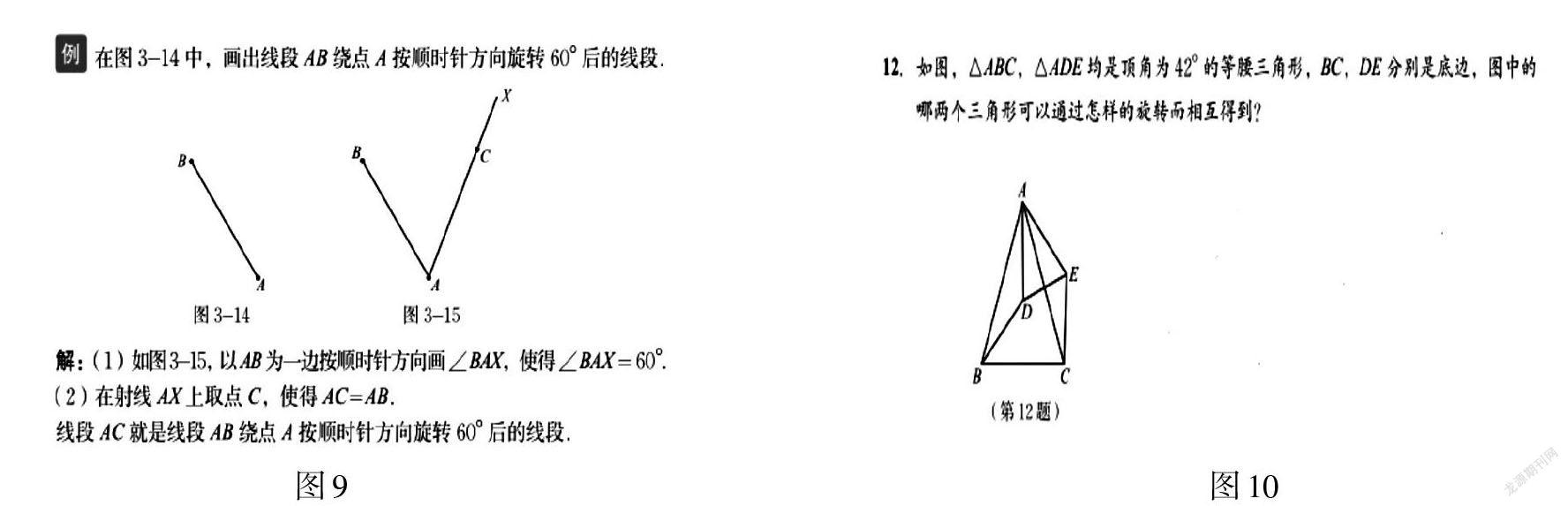
此问中，可以先画出过A、D、E三点的抛物线，再画出过A、D、O三点的抛物线，这样容易结合图形直观发现在对称轴不变的情况下，点G实质上随着点F的运动而运动：点F从点E→O，点G由G→G′，（如图3），这样定点D与动点G连接而成的线段DG与线段AB的交点M又随着G点的变化而变化：点M由M→M′（如图4），从而发现点之间运动的逻辑关系，为第三个问确定点P的运动轨迹作好铺垫。

【评析】首先，本问利用待定系数法求二次函数表达式，运用化归的数学思想方法，将问题简化，难度依然不大，主要考查学生运算能力。其次，在本题中，学生可以多角度观察点的坐标特点，运用不同方法解决问题。最后，画出所求抛物线的图象，通过几何直观也更容易发现点之间的内在联系。

（三）第三问

最后一问的解难度较大，学生会遇到思维障碍。即使原题要求直接写出答案，但实际的分析问题过程体现了这类问题的典型的“化动为静”解题策略，很好地考查学生的推理能力。基于此，笔者对此问进行详细分析：

关键信息：△DMP始终为等边三角形，点F由E运动到O可以挖掘出隐含的条件：60°角、相等的边、三线合一、动点F的始末位置。问题为求点P的路径，会想到求路径首先要明确运动轨迹，因此将求点P的路径问题转化为求点P运动轨迹问题，而在明确点P的运动轨迹之后，再由始末点最终求出点P的路径。但难点在于点P的运动轨迹是什么，又如何确定呢。那么解决这些问题需要突破三道關：读懂“动”——明确动点之间位置关系;找“不动”——抓不变量;怎么“动”——确定动点P的运动轨迹。具体思维过程如下图：

（1）读懂“动”——明确动点之间位置关系

首先，思考本题中都有哪些动点，想想是哪个最先动，哪个最后动，点与点之间是怎样相互牵连着动，并且与所求目标动点P联系最密切的是哪个点。通过审题，不难发现：共有4个动点，点F最先动，从而牵动G点动，而因点G而生的点M最终导致点P动，因此与点P联系最密切为点M，M动牵动着点P动，在这里我们可称之为“主动点”，而点P可称之为“从动点”[2]点P随着动点M的变化而变化。其次，进而猜想，“从动点”P的轨迹与“主动点”M的轨迹应该存在某种特殊关系，具体关系是什么，而M点运动的轨迹又是什么。接下来解决第二个问题。

（2）找“不动”——抓不变量，“化动为静”

点M的轨迹是什么呢？很明显点M在AB上运动，轨迹确定。在动点问题中，常规的解题策略是“抓不變量”。因此，接着“动”中找“静”，即由F的始末固定位置——图4的点E（[0，−43]）与原点，确定抛物线与x轴交点G的始末位置（图4的G、G′），而求G、G′点的坐标可以通过求过E、A、D三点抛物线[y=39x2−3x−43]与过O、A、D三点抛物线[y=33x2−33x]与x轴交点坐标G（12，0）、G′（9，0）确定，进而由DG及DG′与线段AB的交点确定点M的始末固定位置——图4的点M、M′，最终确定点P的始末位置——图6的P、P′点。但需要注意的是，学生容易受数学直觉思维的影响，认为PP′就是点P的轨迹，但其实此时并没有判断出P点的轨迹就是直线。那么接着探究不难发现：

如图6，△DMP始终为等边三角形，点D为定点，即∠MDP始终为60°，就出现了共顶点的等边三角形，那么“手拉手”模型就显而易见了。通过证明△DMM′≌△DPP′，我们从而得出MM′=PP′，∠DM′M=∠DP′P，并且在点运动过程中MM′始终等于PP′，∠DM′M始终等于∠DP′P，这样就相当于又找到了不变的等量关系。

（3）怎么“动”——最终确定动点P的运动轨迹通过“找不动”的解题策略只是确定了MM′=PP′，仍未确定点P的轨迹就是直线，因而继续探究发现：

如图7，动点M向终点H（H为线段AB中点）运动，动点P随之向终点K运动的过程中，始终存在一组全等的三角形——△DKP与△DHM，即∠DKP始终等于∠DHM等于30°（∠DHM=30°，由点H为AB中点，判断出DH//CB，进而得出∠DHM=∠CBA=30°）。即动点P被“绑在”过定点K（K为P最终位置）且与定直线CA夹角为30°的直线上，发现了这个“本质结果”，P的轨迹就确定了。确定了动点P的轨迹后，则由MM′=PP′，动点P的路径迎刃而解。而线段MM′的长可以令直线DG的解析式[y=3x−93]与直线[DG']的解析式[y=233x−83]中x=6就能分别求出M与M′的坐标，求得为M（6，[−43]）、M′（6，[−，33]），所以MM′=PP′=[3]

点P的运动轨迹最终确定实质上采用的是夹角定位法：如图8，已知直线l与定点A，若直线AB与定直线l的夹角确定，则动点B始终在直线AB上，即动点B的轨迹为直线AB。

【评析】此问体现了特殊化的数学方法，将问题引向极端，寻找定点、定线、定角是解决问题的关键，使解题方向更加明确。具体方法是采用夹角定位法，问题解决由浅入深，顺藤摸瓜，环环相扣，在发现点P与点M的关系后，经历猜想与推理论证，得出点P的轨迹是直线，使学生最终突破难点。

五、回顾与反思

（一）思“解法”

根据波利亚《怎样解题》中的“怎样解题表”最后一步“反思回顾”[3]：是否还有其他的解法，有没有更直观的方式说明P点的轨迹一定是直线呢。换个角度，用“旋转”的眼光看动点P，那么会有不同的发现：△DMP始终为等边三角形，即动点P可以看成是动点M绕着定点D顺时针旋转60°而来。因此，所求动点P的轨迹也必然是由动点M的轨迹做相应变换而来，即动点P的轨迹是由MM′绕定点D顺时针旋转60°而来，而由图形的旋转性质可知动点P轨迹也必然是直线。

（二）思“本”溯源

本题的源头可以追溯到“北师大版八下教材”3.2.2节例题（图9），需要应用旋转的性质训练学生解题、画图，识图能力。在北师大版八下教材第96页章末复习题第12题（图10），在观察图形旋转的过程中，进一步训练了学生的识图能力，是典型“手拉手”几何模型的雏形。

（三）思“变式”

1.变条件：

变式一：以线段DM为一边作顶点为D的等腰直角三角形DMP，点P与点A在直线DG同侧，当点F从点E运动到点O时，请直接写出点P运动的路径的长。

变式二：以线段DM为一边作顶点为D，顶角为α的等腰三角形DMP，点P与点A在直线DG同侧，当点F从点E运动到点O时，请直接写出点P运动的路径的长。

2.变结论：

变式三：以线段DM为一边作等边三角形DMP，点P与点A在直线DG同侧，当点F从点E运动到点O时，请直接写出线段PD的最小值。

变式四：以线段DM为一边作等边三角形DMP，点P与点A在直线DG同侧，当点F从点E运动到点O时，求点P运动轨迹的解析式。

【评析】变式是在原题的基础上对条件或者结论进行改变，有利于学生积极主动进行深入的探究，发现基本图形特征和一般规律，总结解决有关题目的通法。做到一题多变，多题归一的教学效果，真正培养学生思维的发散性和灵活性，从而促进学生数学思维能力的发展。

（四）思“教法”

教学中教师要立足教材，落实“四基”，注重识图、作图能力的训练;帮助学生提高解题能力的关键不仅仅在于“怎么做”和“为什么这么做”，更在于多让学生思考“我是怎么想到的”，重视剖析解题思路的形成过程。合理利用变式，达到“一题多解，一题多变，多题归一，多解归一，错例众评”的教学效果[4]。

数学教学要突出数学思想方法，使学生在掌握知识与技能的同时能够自觉有意识地运用数学思想方法，提高解决问题的能力，发展数学核心素养。

[参 考 文 献]

[1]李云萍.说题说出别样天[J].中国数学教育，2015（4）：26-29.

[2]刘彬，徐春艳.例谈“说题”：一次数学“说题比赛”的实录与反思[J].数学通讯，2015（3）下半月：4-7.

[3]波利亚.怎样解题[M].上海：上海科技教育出版社，2001：11-12.

[4]冯剑.在“说题”中经历 在“说题”中提升[J].中国数学教育，2013（3）：45-47.

（责任编辑：杨红波）