牛顿环实验中一些问题的探讨

叶 紫，马文姣，孟子硕，陆振帮

(1.武汉纺织大学 电子与电气工程学院，湖北 武汉 430200；2.武汉纺织大学 数理科学学院，湖北 武汉 430200)

利用牛顿环法测量平凸透镜的曲率半径是一个典型的等厚干涉实验。该实验原理清晰，现象直观，装置简单，能让学生更好地认识光的波动性，理解光学方法在长度测量中的应用。牛顿环实验原理中，有一个重要推导步骤是把理论公式变形为实际测量表达式，而变形原因一般用“中心和级次无法确定”一句带过，未做详述。很多学生在学习本实验时，通常会把它理解为“中心或级次无法确定”，因而会认为教材上用的“和”字有误。本文将详细阐述为什么是“和”而不是“或”，以厘清部分学生的误解。另外，通过对原理公式的分析，本文还指出了线性拟合法在本实验数据处理中的可行性。

1 实验原理简述

1.1 等厚干涉

如图1所示，凸面AB是平凸透镜的下表面，平面CD为平板玻璃的上表面，二者间有一空气薄层。由光源S发出的光线，在AB上的点P处分为两束：一束直接反射回平凸透镜中；另一束折射后进入空气层，在下方CD面上的点R处反射回空气层，最后在AB面上的点T处折射进入平凸透镜中。两束光线在透镜中一点Q相遇，从而发生干涉现象。由于待测凸面曲率半径较大，因而面AB与CD近似平行，故实验中T、Q两点与P点的水平位置基本一致，从而可认为干涉点Q位于凸面AB上。考虑到在CD面上的反射存在半波损失，两束光线的光程差为

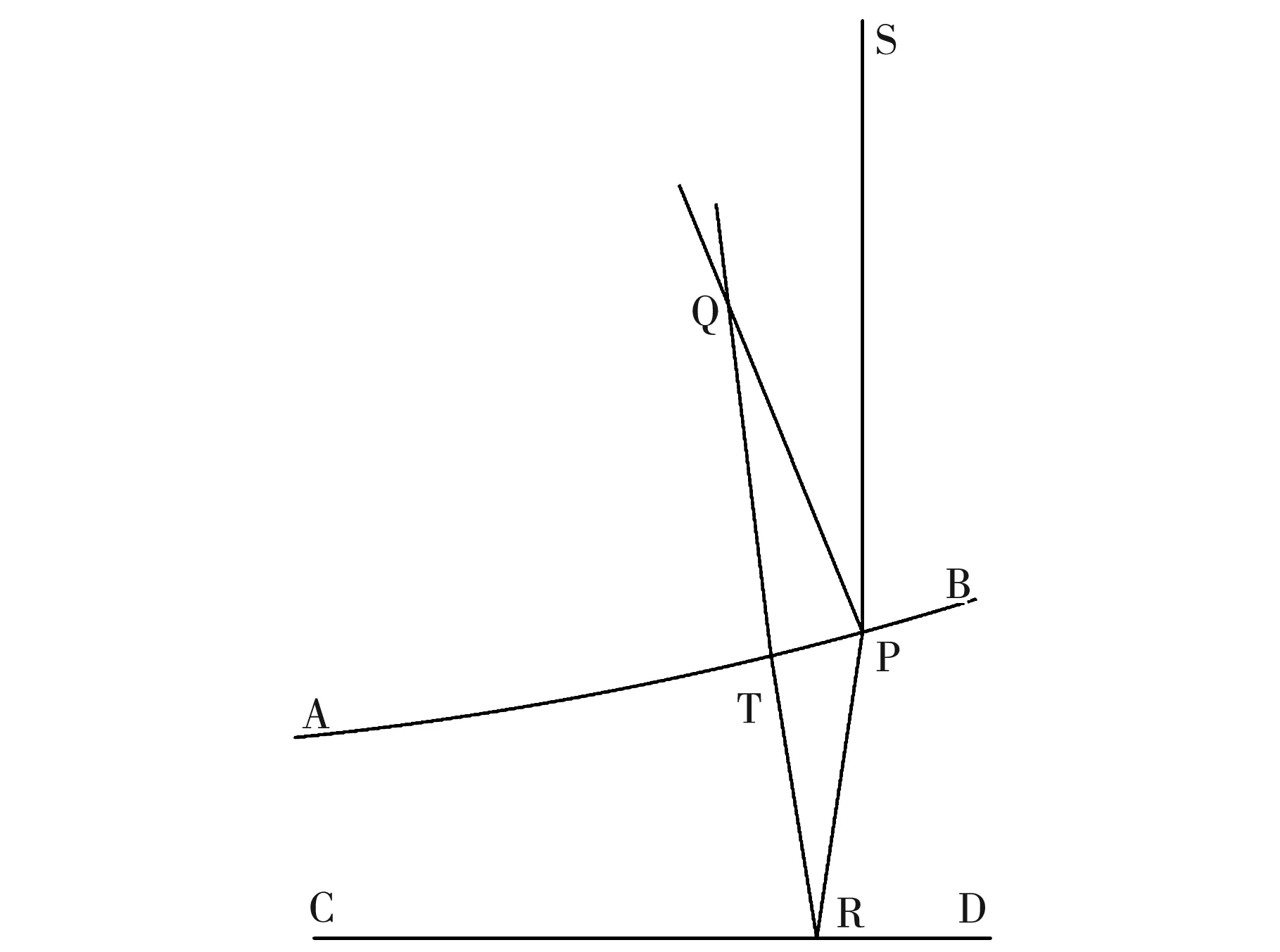
图1 等厚干涉示意图

(1)

(2)

1.2 几何关系

如图2所示，平凸透镜的凸面所在球的圆心为O点，N点为其最低点，P点为凸面上一点，则半径R=ON=OP。若P点处观察到k级暗条纹，则条纹半径rk=MP。H=MN为P点所在平面与顶点N的距离。由于△OMP为直角三角形，故有

(3)

当凸面与平板玻璃相切于N点时，P点处空气层厚度与P点所在平面到N点的距离相等，h=H。将形成k级暗纹的厚度条件(2)式与上式联立，可得

(4)

若已知光的波长λ，测出k级暗纹半径rk即可算出平凸透镜的曲率半径R。

1.3 测量表达式

多数教材在此处都会提一句由于牛顿环的中心和级次无法测定，故(4)式无法直接用于测量[1-5]。需要将式中的半径转换为直径、级次转换为级次差，从而得到最终测量表达式

(5)

笔者所了解到的情况是，很多学生对“中心和级次无法测定”的理解是有偏差的。他们通常的理解是：若凸面悬空放置，不与平板玻璃接触，则环中间的级次无法确定；若凸面与平板玻璃紧密接触，则干涉图案中心是一个大暗斑，从而导致中心无法测定。而凸面与平板玻璃要么不接触，要么紧密接触，两种情形不可能同时发生，故而结论应该是“中心或级次无法测定”。那么，是教材用字不严谨吗？下面我们将对此做出详细说明。

2 中心与级次问题

2.1 中心无法测定的原因

为了弄清这个问题，我们可以做出干涉情况下光强随水平位置变化的图。图3显示的是凸面与平板玻璃相切时的光强分布图。可以明显看出，在中心处干涉相消的不是一个点，而是一个圆形区域。也就是说，无论凸面与平板玻璃是否接触，牛顿环中央都不会是一个暗点(或亮点)，而只会是一个圆斑。这其实是由凸面的几何特性决定的。

在凸面最低点(即图2中N点)处，曲面沿任意方向的斜率为零，要产生明显的厚度变化需要较大的水平距离才行。这就导致了中间部分厚度变化小，干涉光强的变化不明显，从而导致中央处只会是圆斑，而不会是圆点。因此，无论凸面与平板玻璃是相切、紧密接触，还是悬空不接触，牛顿环的中心都是无法确定的。

图2 几何关系图

图3 光强分布图

2.2 级次无法确定的问题

(6)

图4 凸面与平板玻璃不相切时h与H的关系

与(4)式对照可知，不相切带来的问题是公式中的级次k变成了“有效级次”k-c。h0未知，即常数c未知，导致的是有效级次无法确定，也就无法使用(5)式计算出曲率半径R的值。

综合2.1和2.2可知，无论凸面与平板玻璃是悬空不接触还是紧密接触，都存在着牛顿环中心和级次无法确定的问题。教材的表述并无不当，认为是“或”的同学需要加深对原理的理解。

3 问题的解决方案

公式(6)中，在给定波长λ时，需要知道rk和k-c才能算出曲率半径R的值。当中心无法确定时，由半径的定义可知半径无法直接测量。解决办法是改测直径(因为测量直径并不需要知道圆心位置)，公式(6)变为

(7)

对于级次无法确定(即c未知)的问题，解决方案有二种：消除法与线性拟合法。

图5 直径与弦长关系

实际测量中，由于读数显微镜的叉丝中心不一定经过牛顿环的圆心，因而所测的dk可能并不是直径，而是弦长。由图5可知，半径OP与弦长PT之间有如下关系

(OP)2=(PT/2)2+(OR)2，

(2OP)2=(PT)2+(2OR)2.

由于实验中叉丝中心沿直线移动，故OR为一常数。即直径平方与弦长平方只相差一个常数项(2OR)2，这只会给(7)式右端增加一个常数项。无论是对消除法还是线性拟合法，这都不会影响到对曲率半径的测量。

4 结 语

在本文中，我们介绍了牛顿环法测曲率半径的原理，并详细分析了实际过程中的中心和级次问题，说明了在悬空和不接触两种情形下中心和级次都无法确定的原因。另外，还分析了在本实验数据处理中应用线性拟合法的可行性，证明了叉丝中心不过圆心并不会对测量结果带来影响。