BUCK 变换器的模糊滑模积分控制*

王素娥，周超红，郝鹏飞，张 路

(陕西科技大学电气与控制工程学院，陕西 西安 710021)

随着人们环保意识的增强，风能、太阳能等可再生能源受到越来越多的关注，但可再生能源在远距离运输过程中有大的波动[1]，容易受到气候和负载的影响，造成输电系统不稳定[2]。所以，对远距离传输多采用BUCK 变换器进行降压，但由于BUCK变换器的非线性和众多外界因素的干扰，BUCK 变换器输出往往不够稳定[3]，因此需要设计强鲁棒性的控制器，提高BUCK 变换器输出精度。

滑模控制本质上为变结构控制，设计简单，鲁棒性强，多应用于非线性系统[4－6]。但滑模控制开关频率可变存在增加开关损耗的问题[7]，且滑模控制依赖于系统的精确建模，建模不精确导致控制输出存在偏差[8]。而模糊控制与被控对象模型无关，不受系统参数影响，多与滑模控制相结合[9－10]，削弱滑模控制器抖振，提高系统的控制效果。

传统的模糊滑模控制器抖振虽得到降低，但输出存在一定的稳态误差。文献[11]提出通过模糊控制器调整滑模控制器切换项参数来削弱稳态误差，但切换项参数的大小不只影响系统的稳定性，还影响系统稳定时间，两者往往难以同时兼顾。文献[12]提出加入比例积分环节的模糊滑模控制，能有效校正系统的偏差，但比例积分环节只是对输入参数进行运算，并不能消除滑模控制器切换项时变带来的误差，且因滑模控制器结构切换过快，开关管损耗较大。

针对传统模糊滑模控制器输出稳态误差较大和开关管损耗较大的问题，本文提出了一种对模糊滑模控制器输出进行积分的方法。首先建立BUCK 变换器的状态方程，利用滑模控制器跟踪系统运行状态，利用模糊控制器对滑模控制器输出做调整，柔化滑模控制器输出。积分环节对滑模控制器切换项和模糊控制器输出之差进行积分，减小系统稳态误差，并使开关频率固定化，减小系统的功率损耗。

1 BUCK 变换器数学模型

BUCK 变换器拓扑图如图1 所示。图中Vin代表直流电源，V0代表输出电压，V代表开关管两端电压，L1代表滤波电感，C代表滤波电容，R代表负载电阻，L2代表负载电感。VD代表续流二极管两端电压，IL代表滤波电感电流，I0代表负载电流。

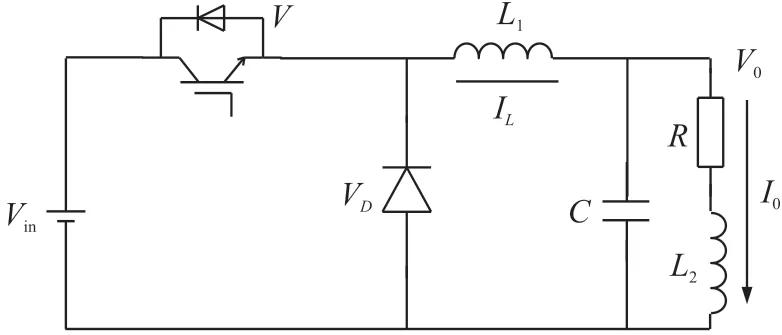
图1 BUCK 型开关电源电路拓扑图

MOS 管开通与关断时，开关管状态有

占空比与输出电流之间的状态方程

为输出电流误差的三阶导数。系统控制框图如图2 所示，滑模控制器输入为x1、x2、x3，滑模控制器输出为等效控制项deq和切换控制项dvss；模糊控制器输入为滑模函数s和滑模函数的导数，模糊控制器输出为uf，uf对滑模控制器切换项做微调；滑模控制器切换项和模糊控制器输出相减，相减之差经过积分环节，积分后的数值与滑模控制器等效控制项相加，对PWM 进行脉宽调制，使输出电流大小维持不变。

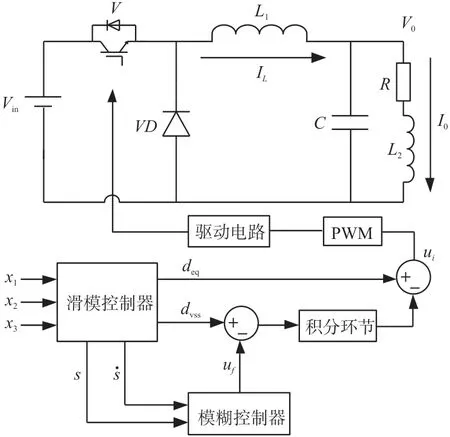
图2 模糊滑模控制系统框图

2 滑模控制器设计

滑模控制器系统结构如图3 所示，其中滑模控制器输出量s为滑模函数，输出量为滑模函数的导数，s与送入模糊控制器做进一步的控制。输出量us为滑模控制器输出。

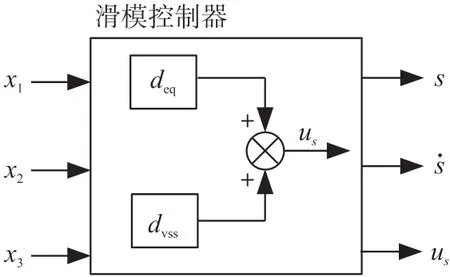
图3 滑模控制器系统结构图

定义误差跟踪函数s为

切换控制率取

式中:ε为切换项系数，且ε＞0

则滑模控制输出控制率为

3 模糊控制器设计

模糊控制器框图如图4 所示，模糊控制器将滑模函数s和滑模函数的导数作为模糊输入。模糊控制器输出uf对滑模控制器切换项dvss进行微调，削弱滑模控制器的抖振。

图4 模糊控制器系统结构图

模糊控制器的输入模糊子集为:PB(正大)、PS(正小)、ZO(零)、NS(负小)、NB(负大)，输出模糊子集为PB(正大)、PS(正小)、ZO(零)、NS(负小)、NB(负大)，采用重心法将模糊输出反模糊化。

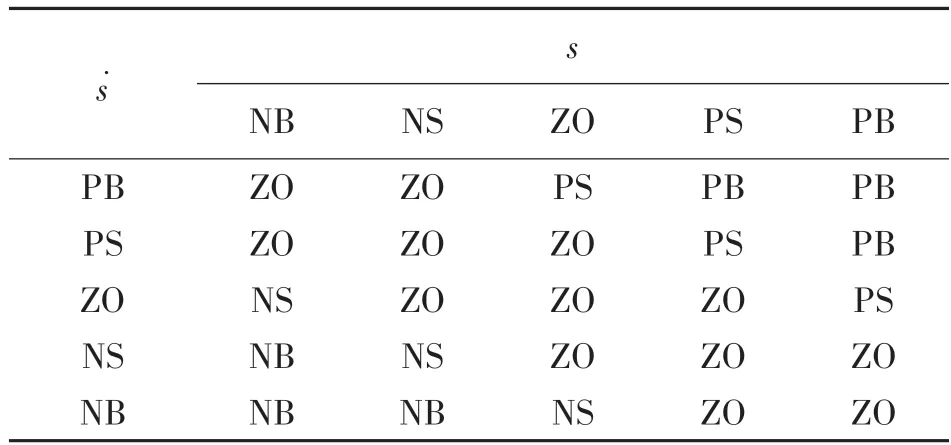
表1 模糊控制规则表

从表1 可以看出，当s和数值都为正大时，则输出uf为正大，以快速减少us的数值；当s与不同号时，系统达到稳定条件，控制输出uf为零。当s与都为负大时，则输出uf为负大，以快速增加us的值。由于模糊控制器是在＜0 的基础上设计的，所以模糊控制器是稳定的。

4 积分环节

滑模控制器等效控制项依赖于系统的精确建模，由于元器件的参数误差，滑模控制器等效控制项实际值与理论值存在偏差，导致系统在稳态时存在控制偏差；滑模控制器切换项依赖于每个周期的状态，存在一定的稳态误差。模糊控制器设计依赖实际经验，在输出上难免存在偏差。因此传统模糊滑模控制器输出往往存在一定的稳态误差。

另外，由于滑模控制器结构不断切换，会给开关管带来很大的开关损耗。假设切换项系数ε为1，其切换状态如式(19)，当s≥0 时，切换控制率为1，当s＜0 时，切换控制率为－1。

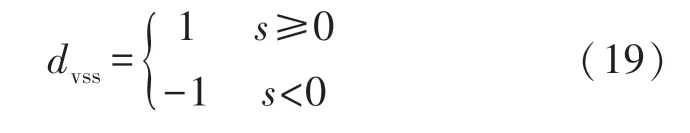
理论上当载波频率一定时，开关管的开关速度不由载波频率决定，而由dvss的切换频率决定，滑模理想工作条件下调制波与载波比较如图5(a)所示，PWM 波形如图5(b)所示。切换项切换速度极快导致开关管开通与关断速度极快。开关管的损耗Psw主要为开启过程的损耗Poff＿on和关断过程的损耗Pon＿off。

图5 理想切换频率下载波与调制波比较图

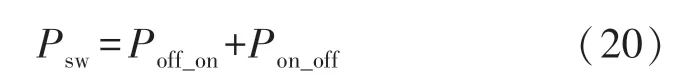
较高的开关速度会带来较大的开关损耗，并且由于元器件实际工作速度的限制，开关管无穷大的开关频率不可能实现，这种速度限制将会改变滑模控制趋于稳定阶段的运动轨迹，导致滑模控制器输出不能精确跟踪滑模控制器输入，带来较大的控制偏差，影响控制效果。

因此，对滑模控制器切换项控制率dvss和模糊控制器输出uf之差进行积分。

式中:ui为积分环节输出。

由于系统稳定后积分数值为一常数值，开关管不再以滑模控制器理想工作频率开通与关断，而是以载波的频率开通与关断，开关管开关频率得到固定，从而将控制无穷大的切换速度转变为调节占空比数值。积分后调制波与载波比较如图6(a)所示，PWM 波形如图6(b)所示。

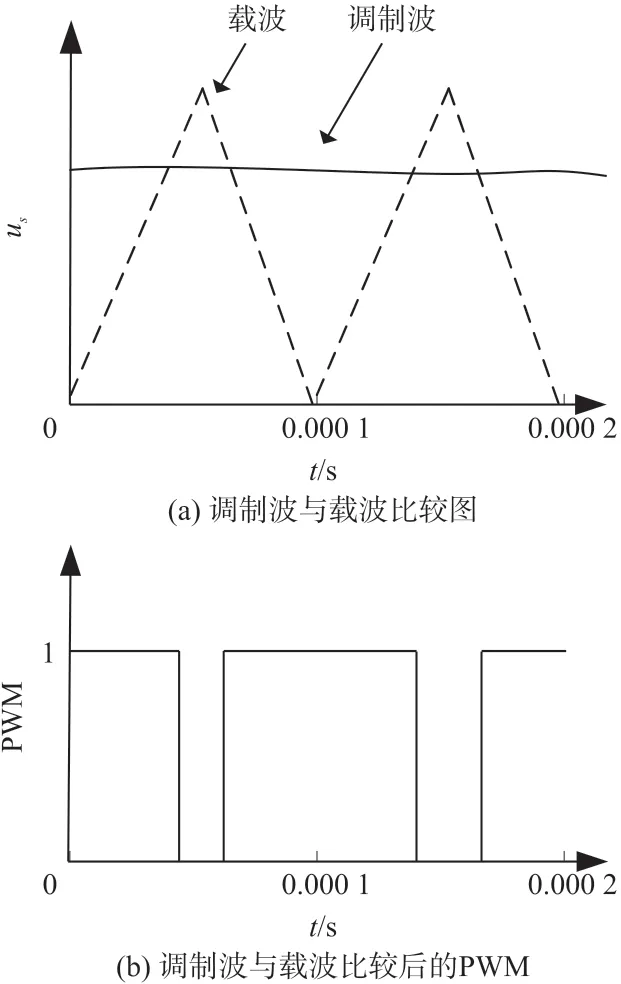
图6 积分后载波与调制波比较图

开关频率固定后，减轻了开关管和元器件的负担，削弱实际控制中由于开关频率达不到滑模理想工作频率而导致的控制器输出偏差。

另外，因积分环节实际上是对过往状态的累积，由于积分项的存在，模糊滑模控制器输出稳态误差得到降低。

5 仿真及实验验证

5.1 仿真验证

采用MATLAB/Simlink 搭建数学模型，电路参数如表2 所示。

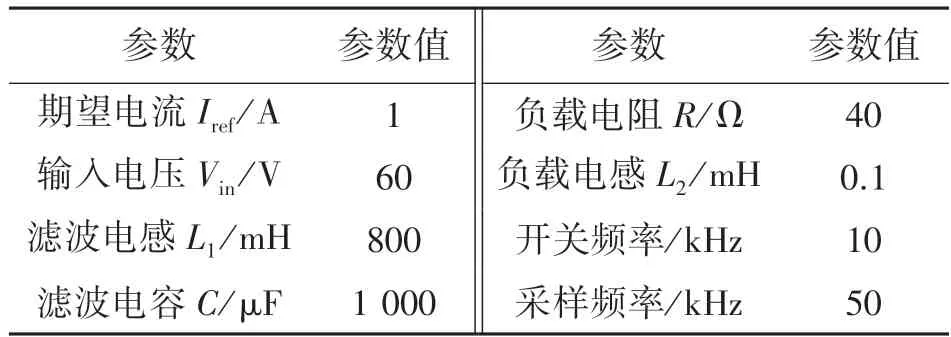
表2 BUCK 电路参数

图7 由上至下分别为传统模糊滑模控制器调制波、载波、调制波与载波比较后的PWM 波形图，左侧为启动阶段波形图，右侧为稳定阶段放大图。由图7 可以看出，传统模糊滑模控制器的调制波切换频率远远大于载波频率，开关频率不定，在1.077 8 s至1.078 s 内(时长为0.000 2 s)PWM 波形变化4次，开关管损耗为4×Psw。

图7 传统模糊滑模控制载波与调制波、PWM 波形

图8 由上至下分别为引入积分环节后模糊滑模控制器调制波、载波和PWM 波形图，左侧图为启动阶段波形图，右侧为稳定阶段波形图。图8 可以看出，在启动阶段调制波有小幅度波动，随后为一稳定的常数值，调制波与载波比较得到的PWM 频率固定为载波频率，即10 kHz。在2.878 8 s 至2.879 s内(时长0.000 2 s)内PWM 波形变化2 次，开关管损耗为2×Psw。

图8 引入积分环节模糊滑模控制载波与调制波、PWM 波形

图9 是传统的模糊滑模控制仿真结果和电流纹波放大图，从图中可以看出，系统稳定后BUCK 变换器输出存在0.03 A 左右的稳态误差，达到稳态的时间约为0.03 s，纹波约为15 mA。

图9 传统模糊滑模控制电流启动仿真结果

图10 所示为引入积分环节的模糊滑模控制仿真结果和电流纹波放大图，由图10 可以看出，BUCK变换器输出为1 A，基本无稳态误差，达到稳态时间约为0.03 s，纹波约为15 mA。

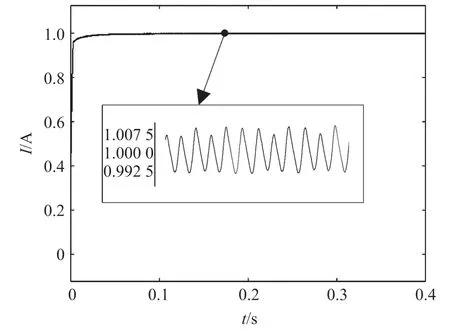
图10 引入积分环节模糊滑模控制电流启动仿真结果

由仿真结果可知，引入积分环节的模糊滑模控制可使PWM 频率固定，从而降低开关管损耗，且稳态误差减小。

5.2 实验验证

搭建BUCK 型变换器试验样机，控制器采用DSP28335，驱动芯片采用HCPL－3120，隔离芯片采用WRB1205S－3WR2，开关管采用CSD19535，其他实验参数见表2。

图11 所示为传统模糊滑模控制的PWM 波形图。由图可知，滑模控制器结构切换的频率时变，导致PWM 频率时变，图11 中示波器时间刻度为一格400 μs，虚线框为两格，即800 μs。在800 μs 时间内，PWM 波形改变10 次，开关管功率损耗为10×Psw。

图11 传统模糊滑模控制PWM 波形图

图12 所示为引入积分环节的模糊滑模控制PWM 波形图，从图中可以看出，PWM 频率固定为10 kHz，占空比有微小波动，从而降低开关管开关频率，图12 中虚线框时间跨度为800 μs。在800 μs时间内，PWM 波形改变8 次，开关管功率损耗为8×Psw，引入积分环节，有效减少了系统损耗。

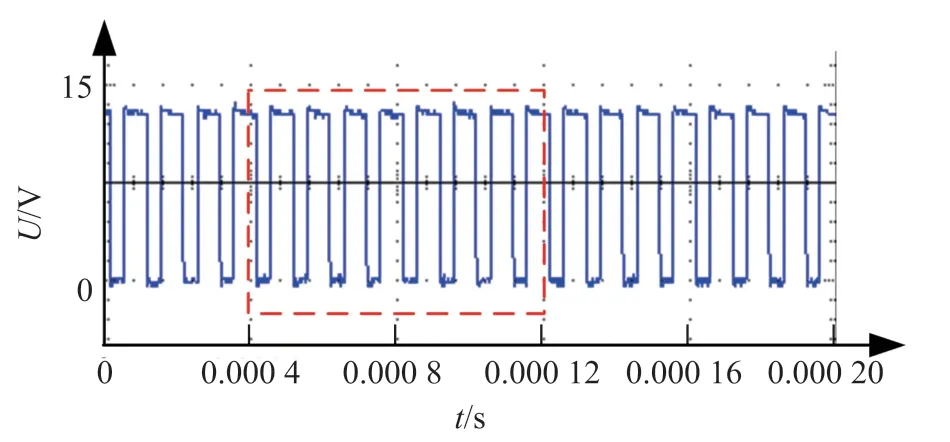
图12 引入积分环节模糊滑模控制PWM 波形图

图13 所示为传统的模糊滑模控制动态响应曲线和纹波。从图13 可以看出，BUCK 变换器输出电流稳态误差约0.08 A 左右，达到稳态时，纹波约60 mA。

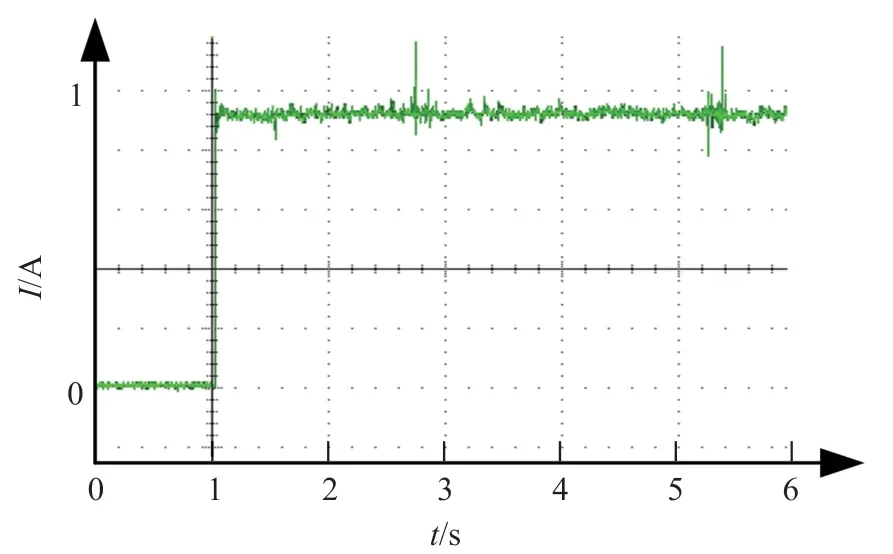
图13 传统模糊滑模动态响应曲线

图14 所示为引入积分后模糊滑模控制的动态响应曲线和稳态纹波。由图可知，BUCK 变换器输出电流为1 A，基本无稳态误差，稳态时纹波约为60 mA。

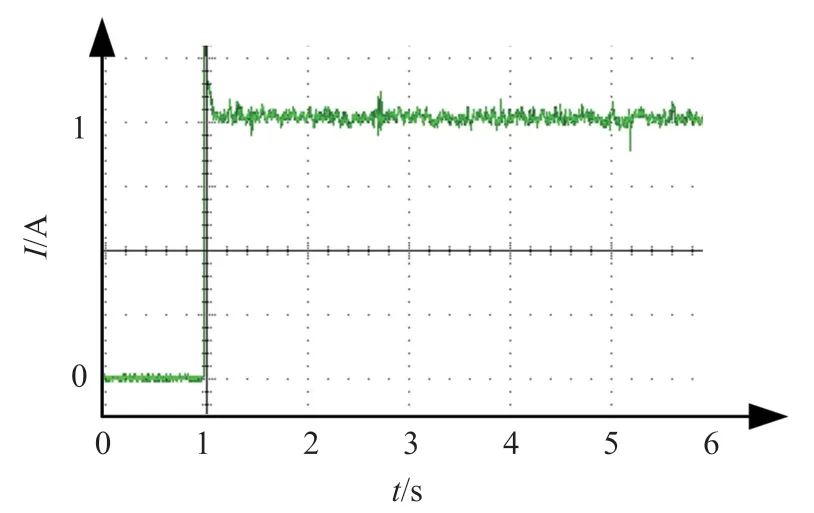
图14 引入积分环节的模糊滑模控制动态响应曲线

由实验可知，传统模糊滑模控制和引入积分的模糊滑模控制稳态时间和纹波相差不大，但引入积分后BUCK 电路输出基本无稳态误差，且开关管开关频率得到固定，降低了开关管功率损耗。

6 小结

本文设计了一种适用于BUCK 变换器的模糊滑模积分控制器。首先建立BUCK 变换器的数学模型，利用滑模控制器跟踪输出电流，利用模糊控制器削弱滑模控制器抖振；积分环节对滑模控制器切换项和模糊控制器输出之差进行积分，使开关频率固定，降低开关损耗，并减小系统稳态误差。

仿真和实验结果表明，相比传统的模糊滑模控制器，引入积分的模糊滑模控制器输出基本无稳态误差，开关频率得到固定，开关损耗得到了有效降低。