MIMO 无线通信系统的随机信道性能分析*

杜文龙 ，黄 余

(1.江苏电子信息职业学院计算机与通信学院，江苏 淮安 223003；2.圣路易斯大学研究生院，菲律宾 碧瑶2600)

多输入多输出(Multiple-Input Multiple-Output，MIMO)通信系统因其巨大的容量而引起了无线通信领域的广泛关注。如果在发射和接收天线之间的衰落是独立的瑞利分布，众所周知，即使发射机没有信道知识，在高发射功率范围，平均容量随发射和接收天线的最小数量呈线性增加[1－3]。然而，在实际场景中，衰落通常不是独立的，会表现出一定的相关性。文献[4－7]表明，信道容量在存在衰落相关性时显著下降，但这些结果是建立在发射机没有信道知识和没有其他分集来源(如时间或频率分集)的假设之上；左世奇等[8]提出了一种新型Massive MIMO 信道模型的统计性建模方法，该模型结构简单、可移植性强，可实现复杂大规模MIMO 移动通信环境中的信道模型构建，适用于Massive MIMO 信道的理论分析以及信道仿真；Zl-Mashade M 等[9]对室内环境下非视距条件下MIMO 信道的混合分集(空间和极化)性能进行了研究，分析了元素间距对交叉极分辨力和共极比的影响。并对混合MIMO 系统的容量和误码率性能进行了分析，且与双极化和空间分集技术进行了比较。仿真结果表明，随着天线间距的增加，混合分集的性能与双极化情况相比有明显的提高。此外，空间分集系统的性能随天线分离度的变化比混合分集系统的性能变化要慢；陈姜高路[10]基于大规模MIMO 的角能量空间形态进行建模，研究了空间选择衰落相关性和莱斯衰落情况下系统信道失效的情况，分析了衰落信道模型对系统性能的影响，提出了通过变化功率分配和基站天线数来有效提高阵列的频道效率；Vu M N 等[11]提出了时间选择性信道在平均发射功率约束下的互信息最大化算法；实际上，如果时间或频率分集在某种程度上可用，则相关衰落可能会得到比非相关衰落更高的信道容量；Vaezi M 等[12]提出了高斯MIMO信道在低信噪比(Signal-to-Noise Ratio，SNR)区域的最佳波束形成；文献[13－14]分析了5G MIMO 通信系统中的频谱效率、分集增益和复用容量，但这一讨论考虑的是单流传输，并没有包括长期平均发射机信道知识的影响。

以上针对MIMO 无线通信系统的研究或者仅针对平稳不相关衰落信道建模，或者仅针对信道容量进行单方面的研究，并未对MIMO 系统在随机信道情形下的总体性能进行分析研究。对此，本文在考虑随机信道的前提下，深入研究和分析了相关性衰落、信道时间选择性和发射机信道知识对信道容量、天线增益和系统截止速率等信息论度量值的影响；仿真实验结果表明本文提出的信道建模模型和性能指标的理论计算是有效和可行的。

1 背景知识和系统模型

MIMO 信息论下的基本概念是将一个数据流分割成多个在单个子信道上并行传输的流。图1 所示为由r个独立和等加性高斯白噪声(Additive White Gaussian Noise，AWGN)子信道构成的通信链路的简单示例，其中r个独立的数据流共享总发射功率PT，并在r个恒定的信道中传输。恒定信道有单位传输增益，且受方差为的高斯噪声的干扰。由于信道的对称性，在r个子信道之间平均分配可用发射功率PT是最理想的，因此系统的容量Cr就是单个子信道容量的总和，即:

图1 多流传输的简单示例

表明了MIMO 系统的容量改进潜力，容量可近似为发射功率的线性函数。在这个示例中，数据流的数量等于发射或接收天线的数量，且所有子信道是独立的，这种MIMO 信道通常称为对角信道。然而，在实际中，MIMO 信道很少是对角的，数据流的数量也不等于发射或接收天线的数量，因为MIMO 信道的秩r决定了支持同时传输的数据流的数量。当信道秩亏时，关系式(2)一般不成立。秩亏实际上可能导致比满秩信道的容量更大，这取决于发射功率。在详细讨论之前，先定义将在文中采用的系统模型。

假设一个频率平坦且可能相关的瑞利衰落无线信道，它通过N个发射天线和M个接收天线来传输L个独立的数据流，于是得到系统模型:

式中:s∈CL为L维数据流向量，有零均值和单位协方差矩阵。是一个正定对角矩阵，用于设置每个数据流的发射功率，由PT＝tr(P)给定总发射功率，其中tr(·)表示求一个方阵的迹(即求对角线元素的和)，矩阵T∈CN×L执行从L个数据流映射到N个发射天线且由单位范数列向量构成，这种映射可以看作是波束形成。信道由矩阵H∈CM×N建模，信道矩阵H中可能存在相关的复零均值高斯项。接收信号向量y∈CM被加性零均值高斯白噪声n∈CM干扰，它对于每个接收天线的功率为。

2 恒定信道及秩亏信道下的容量分析

如果信道矩阵H总是恒定的，则可以假设它对接收机和发射机都是已知的。在这种情况下，通过采用式(4)的奇异值分解可以得到独立的子信道。

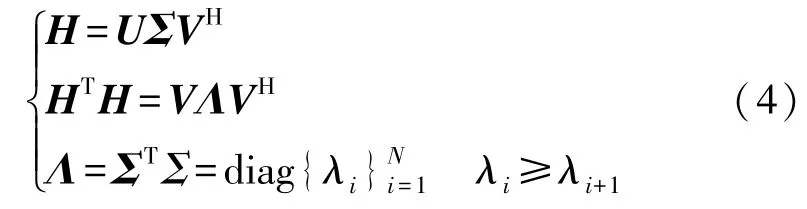
式中:上标H、T 分别表示厄米特转置运算和转置运算，Σ为特征矩阵，Λ为由特征值λi(i＝1，…，N)构成的对角矩阵，diag{·}表示求对角矩阵，U、V为运算矩阵。设T＝V，并应用一对一变换＝UHy，就得到独立的子信道:

式中:为零均值高斯噪声，其方差为，它对于不同的流是独立的。流指标的范围是1≤j≤r，其中r＝H的秩≤min{M，N}，因为对于j＞r，λj＝0。采用注水功率[15]分配Pj＝max(0，μ－)，则信道容量为:

式中:μ是一个正常数，用来满足功率约束tr(P)＝PT。

从式(4)和(6)可以看出，信道容量依赖于Gramian 矩阵HHH的特征值情况(配置)。对于具有平坦特征值情况即λ1＝λ2＝…＝λr＝tr(Λ)/r的系统，令μ＝PT/r＋r·tr(Λ)，于是得到容量:

现在固定信道矩阵H的维数，改变其秩r，为了公平比较，保持所有特征值λj的和即tr(Λ)为常数，仅仅改变信道的秩，同时保持信道总功率不变，如，在这些条件下，有:

对于PT＝γr，式(8)的等号成立。发射功率阈值γr和阈值时的容量Cth，r分别有下限

如果MIMO 系统的优势是用比单输入单输出(Single-Input Single-Output，SISO)系统更低的发射功率提供给定的信道容量，则该结果表明，对于低于Cth，r的期望容量，秩为1 的信道比满秩信道需要的发射功率更低。对于r→∞，秩为1 的信道总是在较低的发射功率下完成工作，而对于有限秩r的信道，它将在低发射功率到阈值γr时正常工作。

3 随机信道下的性能研究

接下来讨论随机信道，其中H为零均值高斯随机变量，建模瑞利频率平坦衰落MIMO 信道，允许信道矩阵元素之间存在相关性，从而导致相关衰落。这种信道可以表现出随机秩亏，意味着相关矩阵有零或有非常小的特征值。

3.1 空间衰落相关性

首先建立相关性模型。一般来说，通过将信道矩阵写成式(10)来建模衰落相关性

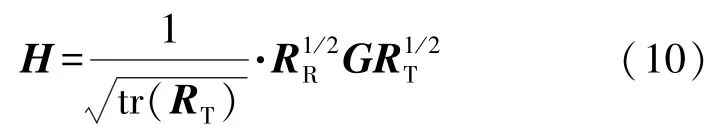
式中:RR＝E{HHH}为M×M的接收相关矩阵，RT＝E{HHH}为N×N的发射相关矩阵，G∈CM×N为独立、零均值单位方差复项的随机矩阵，E{·}表示求数学期望。假设G是从导致相关瑞利衰落的复高斯分布得到，注意到

就是信道的总功率放大，故可以将衰落相关性区分为4 种基本情形:不相关、半相关、半相关2 型和完全相关，如表1 所定义。为简化起见，讨论前2 种情形。

表1 衰落相关类型的定义

3.1.1 不相关瑞利衰落信道

如果发射机和接收机都处在一个散射环境中，就可能产生这样的信道，结果是独立的瑞利衰落从每个发射天线到每个接收天线，于是由

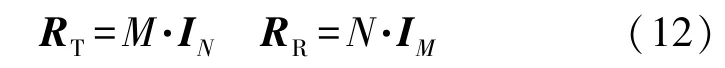
得到H＝G和tr(RR)＝tr(RT)＝M·N。这里In为n×n的单位矩阵。

3.1.2 半相关瑞利衰落信道

如果将发射机从丰富的散射环境中移走，则从发射机的角度来看，现在信道的空间结构受远端散射体的控制，很可能会导致一个高度空间相关的场景，因为通常只有少量的K个远端散射物体占主导地位，所以从发射机的角度来看，信道是空间相关的，由于接收机可以通过两个狭窄的空间方向到达，所以从接收机的角度来看，信道是不相关的，因此有:

式中:A∈CN×K为阵列控制矩阵，它包含对应K个出发方向(Directions of Departure，DoD)的发射天线阵列的K个阵列响应向量，有零均值独立同分布(independent and identically distributed，i.i.d)高斯随机项，应用于式(10)中定义的统计模型得到:

注意，这种信道的总功率放大归一化为tr(RR)＝tr(RT)＝M·N，与不相关情形是相同的。

3.2 样本平均中断容量

信道容量表示系统性能的信息理论上限值。由于所研究的信道通常是时变的，故用随机过程来表示。与文献[10]的方法不同，本文采用的方法是通过恒定发射功率约束，独立于信道状态。为简单起见，以块衰落信道为例，其特性在相干时间Tcoh内保持不变，然后改变为一个新的、独立的实现。这时信道容量依赖于使用时间Tu和相干时间Tcoh的比值。

(1)对于Tu→∞，容量显然由时间平均值¯C给出，或假设遍历性由期望值给出，即所谓的遍历容量Cerg＝E{C}；

(2) 对于Tu＜Tcoh，容量表示就是中断容量Cout(p)，它是在概率等于1－p时可以保证的容量，即Prob{C＜Cout(p)}＝p；

(3)对于Tu＝m·Tcoh，即在Tu内恰好有m个独立的信道实现，我们通过定义一个新的随机变量(Ck为对应于不同信道实现的瞬时容量)，容量就是本节提出的样本平均中断容量Csoc(p，m)，即Prob{Csoc＜Csoc(p，m)}＝p。

其实，样本平均中断容量包含了作为特例的遍历容量和中断容量，因为

一个系统可以通过至少2 种不同的方法实现样本平均中断容量。

(1)自适应编码:根据当前的信道质量改变码率和编码，即当信道良好时，以更高的速率发射。这就要求发射机获取信道的瞬时容量，这可能包括来自接收机的反馈链路建立。这种方法使得在不同信道实现中获得平均容量成为可能；

(2)交错:将码字分散在m个衰落块上，并采用固定速率码。这比自适应编码简单，而且不需要瞬时信道容量知识，但这种方法可能只能实现平均信道容量，通常是一种次优方法，比自适应编码更实用。

3.3 瞬时信道容量

假设第2 节定义的系统模型和完整的接收机侧信道知识，则发射高斯信号s到接收信号y的瞬时互信息Is→y为[3]:

瞬时信道容量就是最大化互信息:

即在给定总发射功率PT的约束下，通过T进行空间处理，通过P进行功率分配来实现最大化。

可以在多大程度上实现互信息的最大化，取决于发射机具有的信道知识，主要分3 种情形。

3.3.1 完整信道知识

假设发射机准确知道每个发射时刻的信道矩阵H，则遵循以下步骤:

(1) 特征值分解(Eigenvalue Decomposition，EVD):HHH＝VΛVH；

(2)设置T＝V，并基于Λ通过注水选择P，使瞬时互信息式(14)最大化。

3.3.2 没有信道知识

另一种极端情形是发射机完全不知道信道，则遵循以下步骤:

(1)设置T＝IN且P＝(PT/N)·IN；

(2)选择最好的结果。

在这种情形下，每个天线发射一个独立的数据流，且数据流之间平均共享功率。

3.3.3 平均信道知识

完整信道知识在实际中可能过于苛刻，假设发射机没有信道知识又可能会过于保守，所以在大多数情形下，发射机应当能够平均获得关于信道的知识。假设知道发射相关矩阵RT，遵循以下步骤:

(1)EVD:E{HHH}＝RT＝V′Λ′V′H；

(2)设置T＝V′，基于Λ′通过注水选择P，最大化Is→y(E{HHH}，T，P)，即平均信道的互信息最大化。

完整信道知识允许最大化平均互信息，平均信道知识允许最大化平均信道的互信息。

3.4 MIMO 天线增益

本节讨论同时考虑多流传输和发射机侧不同信道知识下MIMO 天线增益的计算。

3.4.1 瞬时发射机信道知识下的天线增益

假设接收机无噪声，则对于给定信道H，当HHH＝VΛVH且T＝V时，接收功率PR为:

如果仅使用一对收发天线构成一个SISO 系统，第i个接收天线与第j个发射天线连接，则接收功率为:

取所有可能的接收和发射天线对的平均接收功率，则一个参考SISO 系统的接收功率为:

则瞬时天线增益就是比值PR/P′R，即:

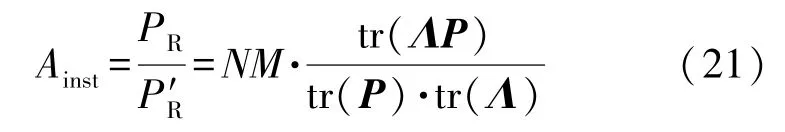
显然，它既依赖于瞬时信道GramianHHH的特征值情况，也依赖于其特征模上的发射功率分配。由于特征值情况依赖于MIMO 信道的接收和发射特性，因此在接收和发射部分不存在天线增益的解耦，这样就可得到天线最大增益为:

如果只加电最强的本征模，即P1＝PT＝tr(P)，将导致单流传输。在低发射功率，注水功率分配就有这种效果。为了更清楚地说明这一点，假设

式中:λ1≤λ2＞0 是信道GramianHHH的两个最大特征值。在这种情况下，实现注水功率分配的容量只会使最强的本征模加电，由式(17)得到的瞬时信道容量变为C＝lg(1 ＋PT)λ1)。由于归一化tr(Λ)＝M·N，则有:

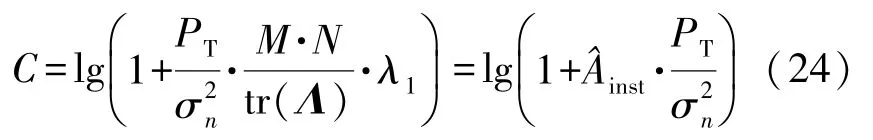
该式表明了在低发射功率时最大瞬时天线增益与信道容量的关系。

3.4.2 长期平均发射机信道知识下的天线增益

在仅有长期平均信道信息对发射机可用的情况下，当RT＝V′Λ′V′H和T＝V′时，MIMO 天线增益基于平均接收功率:

在同一MIMO 信道的两个天线上工作的SISO系统在不同天线对上得到的平均接收功率为:

于是可得天线的长期平均增益为:

与瞬时情形相比，可以很容易地解耦成接收和发送部分:

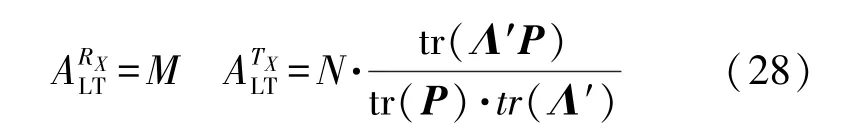
因为发射相关矩阵RT的特征值配置仅仅是MIMO 信道的发射端随机特性的函数。对于单流传输，获得的最大长期天线增益为:

注意M≤≤NM，在不相关情形下取下界，其中RT是一个缩放单位矩阵。当RT的秩为1 时，得到最大天线增益＝NM。在实际中，如果仅通过一个单一的散射体就能到达移动站，且角度扩散足够小，就可能出现这种情况。对于低发射功率，最大长期天线增益与平均信道容量也有一个简单的关系。对于

3.4.3 无发射机信道知识下的天线增益

如果发射机没有信道状态信息可用，则由均匀功率分配P＝(PT/N)IN得到天线增益为:

这完全取决于接收天线增益，发射机侧天线增益的激活至少需要关于信道的长期信息。

3.5 截止速率

尽管容量是无限块长度码和零误差概率的理论极限，但截止速率给出了有限块码长和误差概率的界限。假设采用(n，k)q个分组码，根据截止速率定理[16]，则在最大似然解码后的码字错误概率Pw的上界为，这时二进制码率Rb＝k/n·log2q小于截止速率

式中:M(｜M｜＝q)为输入码元集合，p(y｜s)为给定发射码元s下接收信号y的概率密度函数。为了将其应用到本文的MIMO 系统中，我们将数据向量s视为一个q－进制码元符号，其中每个元素sk(1≤k≤L)可以从离散调制字母表Mk中取qk个值，这里｜Mk｜＝qk。输入字母M＝M1×M2×…×ML是单个字母集的笛卡尔积，这里｜M｜＝q＝q1·q2·…·qL。通过标记M＝{s1，s2，…，sq}的元素，于是瞬时截止速率可计算为:

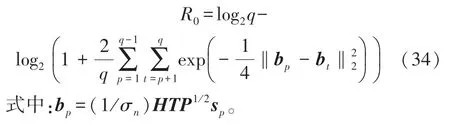
4 仿真实验

4.1 实验设置

为了对本文的研究结果进行仿真验证，在MATLAB/Simulink 仿真环境中采用如图2 所示的实验装置；对于信道容量和天线增益的仿真实验，仿真一个M＝N＝8 的天线系统，其中天线形成一个全向均匀线性阵列，并对一个4 路半相关信道和一个不相关信道作为比较。4 路路径的传播角度为零，出发方向随机。对瑞利衰落路径系数和随机出发方向均进行平均，其中随机出发方向假设在－90°，…，90°的方位角范围内均匀独立分布；对于系统截止速率的仿真实验，仿真一个由N＝2 个发射天线、相隔半个波长和M＝2 个接收天线组成的系统，系统在一个不相关信道或在一个一路半相关信道上工作。注意，如果与发射阵列的标准波束宽度(在本例中波瓣宽度为60°)相比，角度扩展较小，则发射协方差矩阵将有秩亏。在半相关情形下，将区分无发射机信道知识和平均发射机信道知识；未编码(原始)比特率固定为rraw＝4比特/每路使用。对于不相关情形，采用4－正交调幅(quadrature amplitude modulation，QAM)并在每个天线上一次发射两个独立的数据流，对于没有信道知识的半相关情形同样成立；另一方面，如果发射机有平均信道信息可用，则秩亏可以转化为天线增益。因此，只有一个单一数据流将通过主特征波束发射。为了实现相同的原始比特率，调制方案改为16－QAM。

图2 仿真实验装置

4.2 仿真实验结果

4.2.1 信道容量

本节仿真实验评价具有和不具有平均信道知识的不相关和半相关瑞利衰落信道的容量，图3 和图4所示为得到的结果。

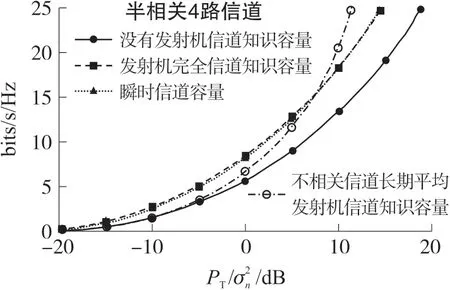
图3 具有和不具有平均信道知识的不相关和半相关瑞利衰落信道的遍历容量和瞬时信道容量的比较

图4 具有和不具有平均信道知识的不相关和半相关瑞利衰落信道的中断容量和瞬时信道容量的比较

从图3 和图4 的结果可见:

(1)在没有发射信道知识的情况下，相比于不相关情形，空间相关性会降低容量，在有时间分集(遍历容量)和没有时间分集(中断容量)的情形下确是如此；

(2)如果采用平均发射信道知识，对于低发射功率直至一个交叉点，半相关瑞利衰落信道的确比不相关信道能提供更高的容量，这对于遍历容量和中断容量都是如此；

(3)对于半相关瑞利衰落信道，平均发射信道知识和完整发射信道知识的差别是很小的，且在高发射功率，差别会消失，即使对于中断容量来说也是如此，尽管没有额外的时间或频率分集可用，平均信道知识在实际中也足够了；

(4)由于秩满信道，在高发射功率采用不相关信道相比于半相关信道变得越来越好。但要注意，任何真正的通信系统将不得不采用有限的星座大小调制方案，这将限制可实现的容量。

4.2.2 平均瞬时天线增益与长期平均天线增益

由于信道H是一个随机变量，因此天线瞬时增益也是一个随机变量，所以比较它的期望值E{}和长期平均天线增益才是有用的。如果H∈CM×N是一个具有零均值i.i.d 分量的复高斯矩阵，则矩阵HHH的平均最大特征值有上界:

从这个结果得到:

即不相关信道的平均最大瞬时天线增益的增长比接收和发射天线数量的乘积慢得多。另一方面，相关衰落MIMO 信道的长期平均天线增益对于秩RT＝1 取值＝M·N，这就解释了在处理相关衰落MIMO 信道时，在低发射功率区域获得性能增益的可能性。这种效应随着天线数量的增加而增强，图5 所示为仿真结果，这里假设接收和发射天线数量相等。显然，相关衰落中的长期平均天线增益比不相关情况下的平均瞬时天线增益大，这是因为发射相关矩阵有显著的秩不足。注意，对于低发射功率，单流传输是可以获得容量的，这使得天线增益成为低功率区域的一个重要问题。另一方面，在高发射功率区域，天线增益不再是一个理想的值，因为真正的多流传输是需要获得容量。

图5 不相关信道的平均瞬时MIMO 天线增益(E{Ainst})和长期平均MIMO 天线增益(ALT)的比较

4.2.3 系统的截止速率性能评价

通过对实际调制方案和天线数目的截止速率的评价，可以对相关衰落中MIMO 系统的性能有一定的了解，图6～图8 为得到的结果。对于图6 来说，由于中断截止速率描述的是没有时间或频率选择性的情形，所以分集的唯一来源是空间，因此，不相关信道的性能优于半相关信道。然而，在这种特定的场景中，半相关信道在高发射功率区域而不是在低发射功率区域优于不相关信道；对于图7 来说，样本平均中断截止速率描述了一种具有一定时间或频率可选择性的情形，这种情形更有利于在发射机端具有长期平均信息的半相关信道。显然，在低发射功率区域衰落相关性变得有利；对于图8 来说，这相当于无限样本容量下的样本平均中断截止速率，即无限时间或频率选择性。可见，在发射机端具有长期平均信道信息的半相关信道在几乎所有发射功率和编码速率下都具有良好的性能。

图6 不相关和半相关瑞利衰落信道的中断截止速率比较

图7 不相关和半相关瑞利衰落信道的样本平均中断截止速率(样本大小为10)比较

图8 不相关和半相关瑞利衰落信道的遍历截止速率比较

总之，图6～图8 的结果表明:

(1)不相关信道在没有时间分集的情况下表现最好，这从中断截止速率可以看出；

(2)可用的时间分集越多，即在通信时间内可用的独立信道实现越多，则半相关信道就越有吸引力；

(3)如果没有发射信道知识，无论有多少时间分集可用，半相关信道有最差的性能；

(4)具有平均信道知识的发射机，半相关信道会得到最好的性能—事实上，如果有足够的时间分集可用，它的性能会超过不相关信道；

(5)如果在通信时间内独立信道实现的数量进一步增大，则遍历截止速率表明，半相关信道的优势仍在不断改进和扩展，几乎适用于所有编码速率。

5 结束语

MIMO 系统的容量依赖于信道的统计特性和关于这些特性的知识，这对于没有发射机信道知识的相关衰落是一种劣势，特别是如果没有其他形式的分集(如频率或时间)可用时；让发射机获得信道的平均特性，实际上可以导致不相关衰落信道的容量提高，但在相关衰落下，天线增益会比不相关情形大，这将导致在低发射功率下相关MIMO 信道性能的提高。在高发射功率区域，由于多流传输和更高的空间分集带来的容量增益优于天线增益，因此衰落相关性降低了性能；截止速率表明，对于线性调制方案，如果除了纯空间分集外，还存在适当的时间或频率分集可用，则半相关衰落信道有潜力在一个有用的发射功率范围内提供优越的性能。