基于多变量GAMLSS模型的洪水理论分布研究

邢贞相，刘昊奇，刘明阳，喻 熠，李 根，王红利，李 衡，付 强，纪 毅

（东北农业大学水利与土木工程学院，哈尔滨 150030）

洪水频率分析作为建设水利工程重要参考指标，受到设计人员和学者广泛关注[1]。一般情况下，计算工程设计洪水时主要使用P-III 分布进行分析，而随着气候变化和人类活动影响，流域水文系统已发生明显变化[2]，洪水序列不再满足一致性假设要求[3]，这种传统方法无法大范围适应现阶段环境下洪水频率分析计算运用。因此，对于设计洪水的计算，除直接分析洪水序列自身统计规律外，还应考虑其他相关影响因素，例如，气候条件影响、下垫面变化及其对序列一致性假设的影响等，从多方面降低序列非一致性对设计洪水计算的误差，提高洪水频率计算成果科学性。

针对非一致性条件下洪水频率分析，国内外学者开展一系列探索，主要从以下3 个方面研究。①关于洪水序列的非稳定变化趋势研究，江聪等选取宜昌站洪峰流量序列，利用GAMLSS模型分析其趋势[4]；Machado等基于非平稳洪水频率条件下分析西班牙中部塔霍河洪水数据[5]；Villarini 等收集美国50个气象站洪峰数据，分析20世纪年最大洪峰变化情况[6]；宋松柏等将全概率公式应用到频率分布中，计算具有跳跃变异的非一致水文序列[7]。②关于洪水序列随机特征研究，Singh等考虑到洪水序列不确定性，提出混合分布概念，用于美国伊利诺伊州33条河流洪水频率分析计算[8]；谢平等提出时间序列分解和重构原理，计算合成序列频率分布[9]；Hosking 等利用蒙特卡罗模拟方法，探讨区域概率加权矩算法在区域洪水频率分析中的应用[10]。③考虑洪水序列外生因子的影响，Grimaldi 等利用copula 函数计算多变量条件下设计洪水联合概率分布[11]；Rigby 等提出GAMLSS 模型，分析时间序列[12]；顾西辉等将气候因子和水库指标纳入洪水频率分析中，分析变化环境下东江流域非一致性洪水频率[13]。通过上述非一致性洪水频率计算理论和方法研究，使洪水频率计算不再局限于水文一致性假设的前提，且从多因素多角度考虑水文非一致性的影响，拓展传统洪水频率计算理论和应用范围。

汤旺河流域作为黑龙江省较典型的丘陵植被相互交错地带，洪水形成过程复杂多变，流域基础资料和洪水数据较完备，因此适宜研究洪水频率计算。本文利用GAMLSS模型，引入时间和降水作为协变量，建立单变量和多变量分布模拟体系，优选各站年最大洪峰、一日洪量、三日洪量及七日洪量理论分布，分析洪水实测点据与理论分位曲线关系。为考虑历史特大洪水影响频率计算，解决历史特大洪水无相应降雨资料问题，利用洪水序列、气候因子与降水的相关特性，构建H2o深度学习模型，预测历史特大降水，用以确定历史特大降水量值。

1 研究方法

为建立分布模拟体系和预测历史特大降水，本文使用GAMLSS模型和H2o深度学习模型开展计算，具体原理方法介绍如下文所述。

1.1 GAMLSS模型

定义某一时刻t(t=1,2,…,n)相互独立观测值yt服从概率密度函数，其中θt=（θt1,θt2,…,θtp）为时刻t对应的分布参数向量，m为分布参数个数，n为观测值个数。实际计算中，m一般最多取值为4，即θt=（θt1,θt2,θt3,θt4）=（μi,σi,νi,τi），其中μi表示为位置参数，σ表示为尺度参数，νi和τi表示为形状参数（如偏度参数和峰度参数）。

另设y=（y1,y2,…,yn）T为独立观测值yn组成的时间序列，令gk(·)作为将分布参数与解释变量相关联的单调链接函数，表示方法如下：

θk为所有时刻第k个分布参数组成的向量，θk=（θ1k,θ2k, …,θnk）T，k=1,2,…,4。记gk(·)表示θk与相应解释变量Xk和随机效应项之间单调函数关系，一般表示为：

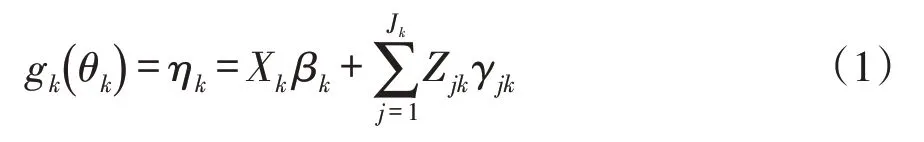
式中，θk为时间序列第k个分布参数组成的向量，ηk均为长度为n的向量(k=1,2,…,4)，βk=为长度为Ik的回归参数向量，Xk为n×Ik的协变量矩阵，Zjk为n×qjk固定设计矩阵，γjk是一个qjk维的服从正态分布的随机变量向量，Zjkγjk表示第j项随机效应项，qjk表示第j项随机效应中随机影响因子维数。

如果不考虑随机效应对分布参数的影响，即对于k=1,2,…,4 时，令Jk=0，则GAMLSS模型变成一个全参数模型：

引入不同位置、尺度、形状参数后，公式（2）可表示为：

当主要研究随机变量分布参数变化与协变量x关系时，解释变量矩阵可表示为：

将公式（4）代入公式（3），则可得分布参数与时间变量函数关系：

GAMLSS模型采用极大似然法（Maximum likeli⁃hood Estimation，MLE）估计回归参数β，似然函数为：

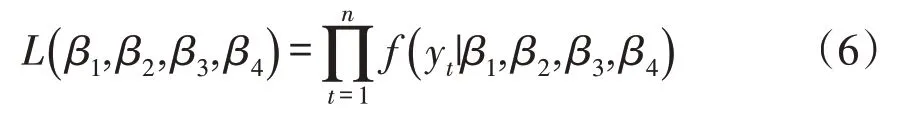
参数估计可利用RS算法（Rigby and stasinopou⁃los algorithm）和CG 算法（Cole and green algorithm）估计回归参数β最优值，本文主要采用RS 算法。

1.2 H2o深度学习模型

与传统人工神经网络（ANN）[14]模型不同，深度学习模型通过大数据分析，加强训练的运行速度、稳定性和可扩展性。在解决不同问题上深度学习模型表现良好，成为预测精度最高的算法，并运用于认知模拟、规划和问题求解、数据挖掘、网络信息服务、图象识别、故障诊断、机器人和博弈等领域。

本文利用R 语言接入H2o 平台[15-17]，通过建立深度学习模型[18-19]预测历史特大降水。该平台核心代码基于JAVA 编写，算法在H2o 分布式Map/Re⁃duce 框架[20]下实现，并利用Java Fork/Join 框架[21]作多线程处理。数据以并行方式读取，将其分布在整个群集中，以压缩格式存储于内存中。建模时结合自动数据标准化、自动适应学习率、自动性能优化，便于合理利用计算机性能。

2 实例应用

2.1 流域概况

汤旺河流域概况如图1所示。

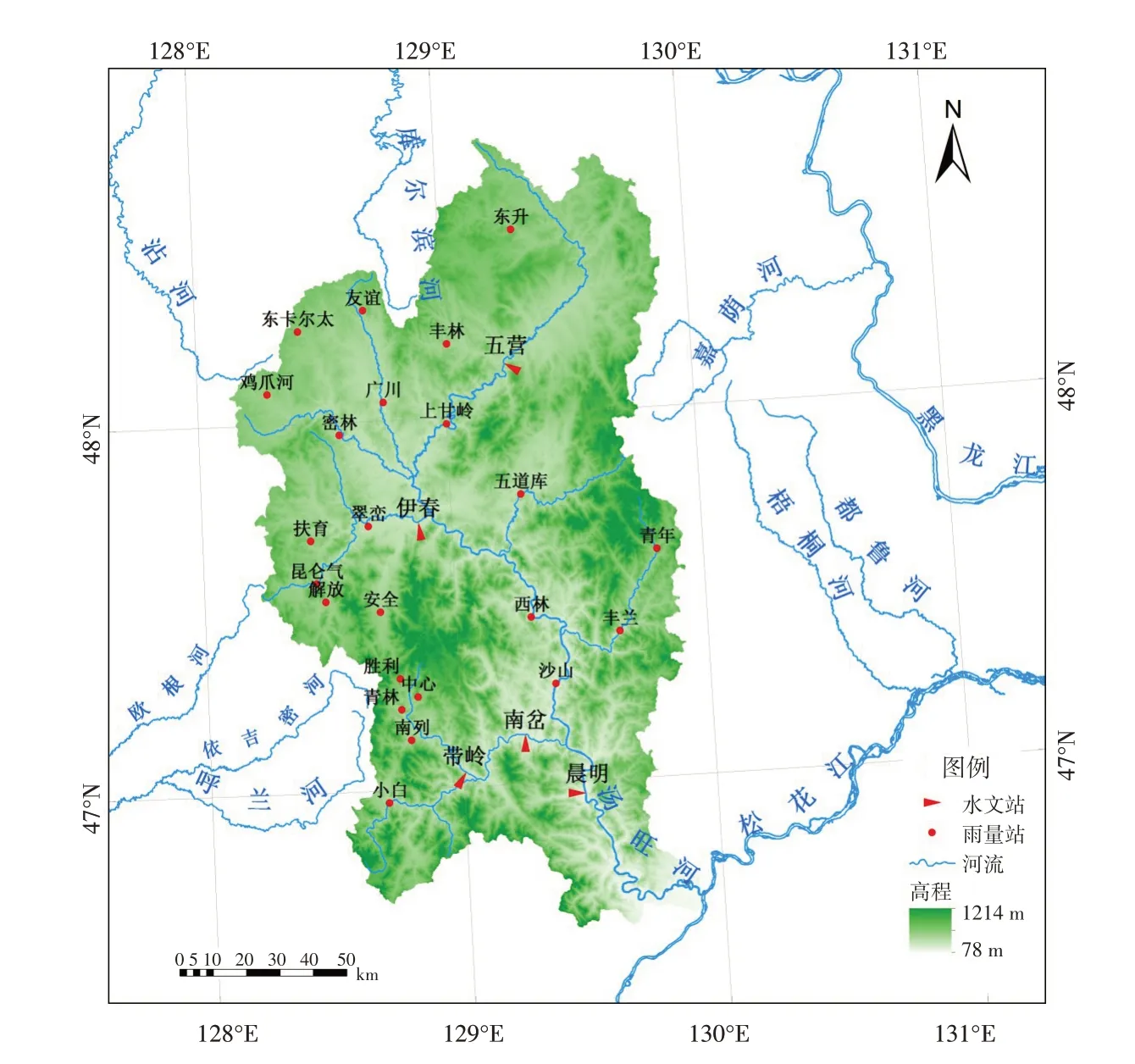
图1 汤旺河流域概况Fig.1 General map of Tangwanghe Basin

汤旺河流域发源于黑龙江省小兴安岭中北部（东经128°51′～130°8′，北纬48°22′～48°48′），是松花江下游的一条主要支流。汤旺河全长509 km，流域总面积约2.1 万km2，地形多低山、丘陵和谷地，起伏较大，是典型的山溪性森林流域。流域多年平均降水量600 mm，降水主要集中在6～9月，短历时降水量较大，地形条件复杂，易发生自然性洪水灾害。

2.2 数据来源

2.2.1 水文数据

选取汤旺河流域晨明、带岭、南岔、五营、伊春共5 个水文站的年最大洪峰（Q）、不同时段年最大洪量（W1、W3、W7）数据和历史特大洪水数据，其中洪水数据来源为黑龙江省历年水文年鉴》，历史特大洪水数据来源为《黑龙江省历史大洪水》[22]。

2.2.2 降水数据

选取汤旺河流域内23 个雨量站年最大1日降水（R1）、年最大3日降水（R3）数据，并对点降水数据作预处理，插补各缺测年份，将单站点雨量数据转化为面雨量数据。该数据均来源于黑龙江省历年水文年鉴。

2.2.3 气候因子

通过开源网站，下载各年NAO、PDO、WP、NOI、AO共5种月尺度气候因子指标，各气候因子数据来源如表1所示。

表1 气候因子数据来源Table 1 Climate factor data source

3 结果与分析

由于水文事件是一个包含频域、时域和空间域的复杂过程，单变量很难描述水文事件真实特征[2]。因此本文分别考虑单变量和多变量洪水频率分析，对比优选分布结果，分析不同条件下模型模拟结果变化。

本研究主要选取水文中常用7种两变量概率分布类型，包括伽马分布（Gamma，GA）、耿贝尔分布（Gumbel，GU）、对数正态分 布（Lognormal，LN）、逻辑斯谛分布（Logistic，LO）、正态分布（Normal，NO）、韦布尔分布（Weibull，WEI）、广义帕累托分布（Generalized pareto，GP）。

为得到上述分布最优参数，GAMLSS 模型通过广义AIC 准则（Generalized akaike information criterion，GAIC）评价所选取模型拟合优度，以AIC最小值为参数优化准则，并通过计算残差序列均值、方差、偏态系数、峰态系数、Filliben 相关系数检验分布的拟合效果。如果满足残差均值接近0，方差接近1，偏态系数接近0，峰态系数接近3，在给定的95%显著性水平下，Filliben系数越大且接近1，表明该残差序列符合标准正态分布，模型拟合效果较好。

3.1 单变量洪水频率分析

以AIC 最小值作为Filliben 系数大于等于一定标准值，表明该残差序列符合标准正态分布，模型拟合效果较好。评价准则，选取各站Q、W1、W3、W7最优分布。表2 列出单变量最优分布及残差评价指标结果，最优分布选取除南岔站W7为GA，其余各站均为LN。残差序列除五营站偏态系数和峰态系数偏差稍大外，其他4 站残差序列均值区间为-0.002～0、方差区间为1.015～1.022、偏态系数区间为-0.201～0.353、峰态系数区间为2.100～3.194、Filliben 系数区间为0.987～0.996，各指标均符合其相应优选标准。

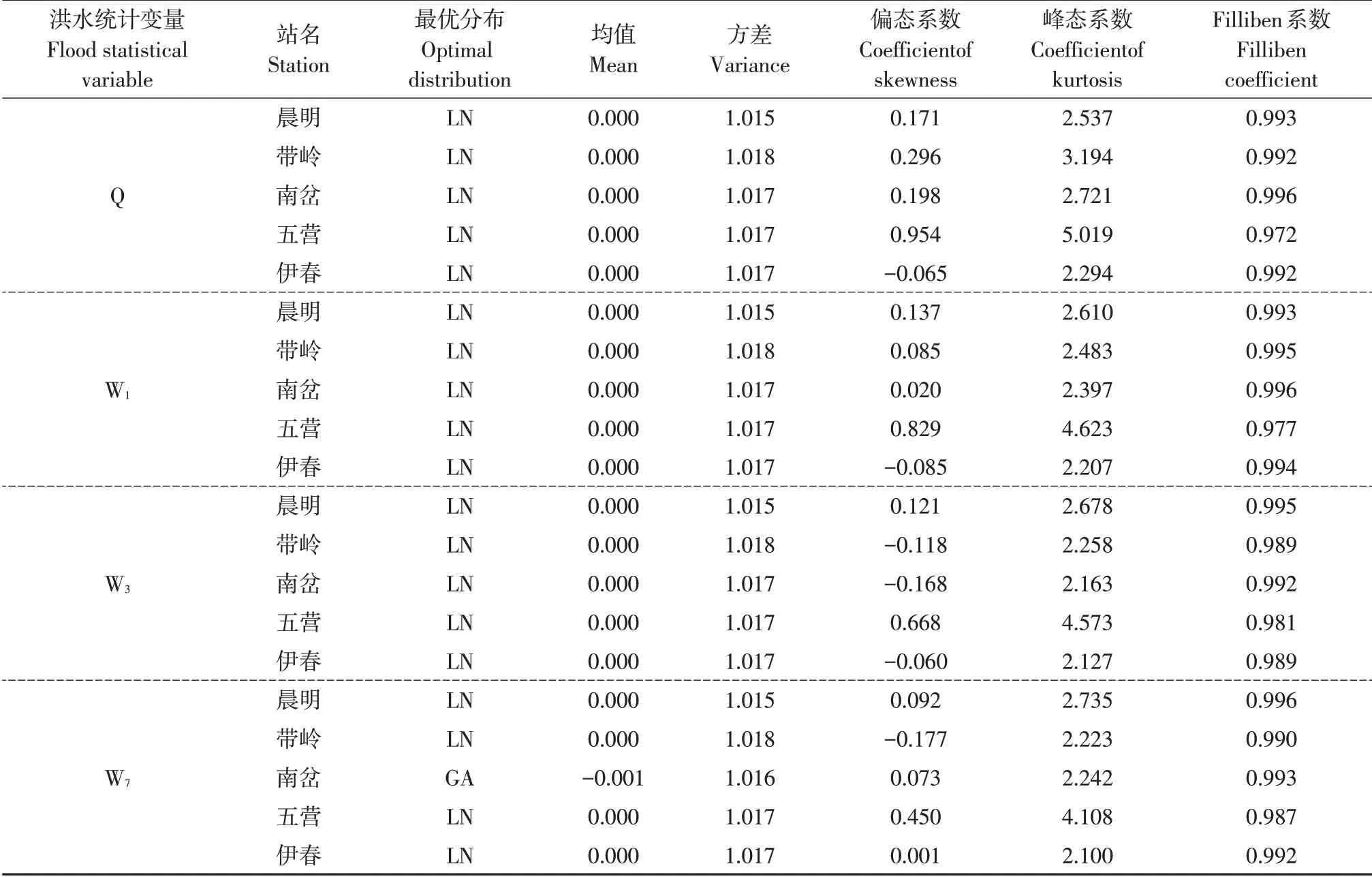
表2 单变量残差评价指标Table 2 Univariate residual evaluation index

以晨明站为例，各洪水统计变量理论频率曲线与经验频率曲线（经验点据的光滑曲线）拟合结果如图2所示。

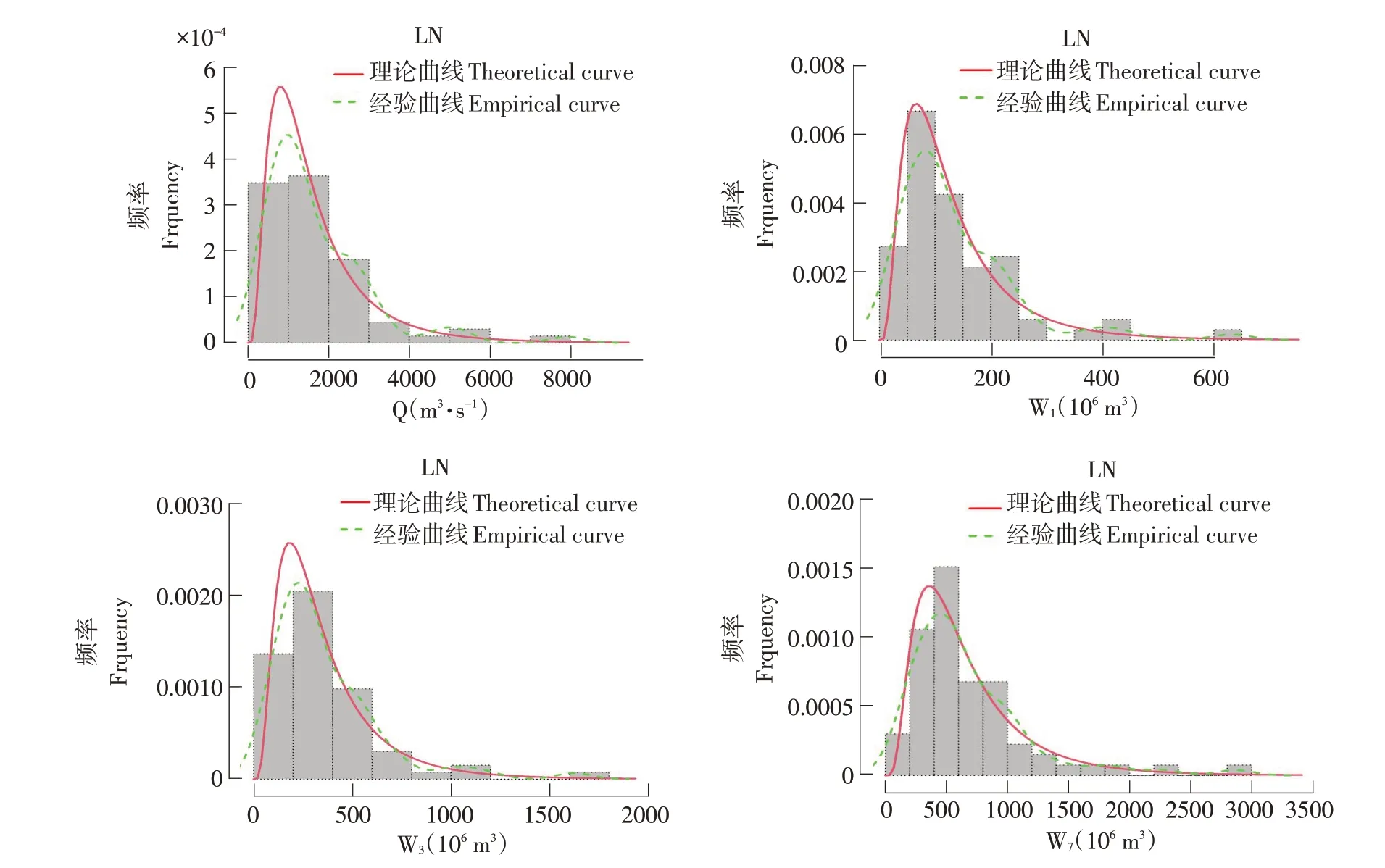
图2 晨明站各统计变量频率直方图、经验频率曲线与理论分布曲线Fig.2 Frequency histogram,empirical frequency curve and theoretical distribution curve of each statistical variable at Chenming Station

由图2可知，不同洪水统计变量经验频率曲线（虚线）与理论频率曲线（实线）拟合效果均较好，且最优分布均为LN 分布（限于篇幅其他分布拟合效果图从略），故选用该分布为晨明站洪水频率分析的最优分布。

3.2 多变量洪水频率分析

3.2.1 时间协变量

以时间为协变量，通过AIC评价准则，对洪水各统计变量理论分布进行优选。表3列出以时间为协变量的最优分布及残差评价指标结果，最优分布选取除晨明站W1、W3、W7和伊春站Q为GA，其余各站均为LN。各站残差序列均值分布在-0.012～0.018，方差分布在1.013～1.018，偏态系数分布在-0.204～0.555，峰态系数分布在2.107～3.476，Filliben 系数分布在0.985～0.996，该结果表明引入时间协变量后GAMLSS模型优选分布和拟合效果不同于单变量（见表2），且各残差评价指标略有变化，但各指标值精度均较高。

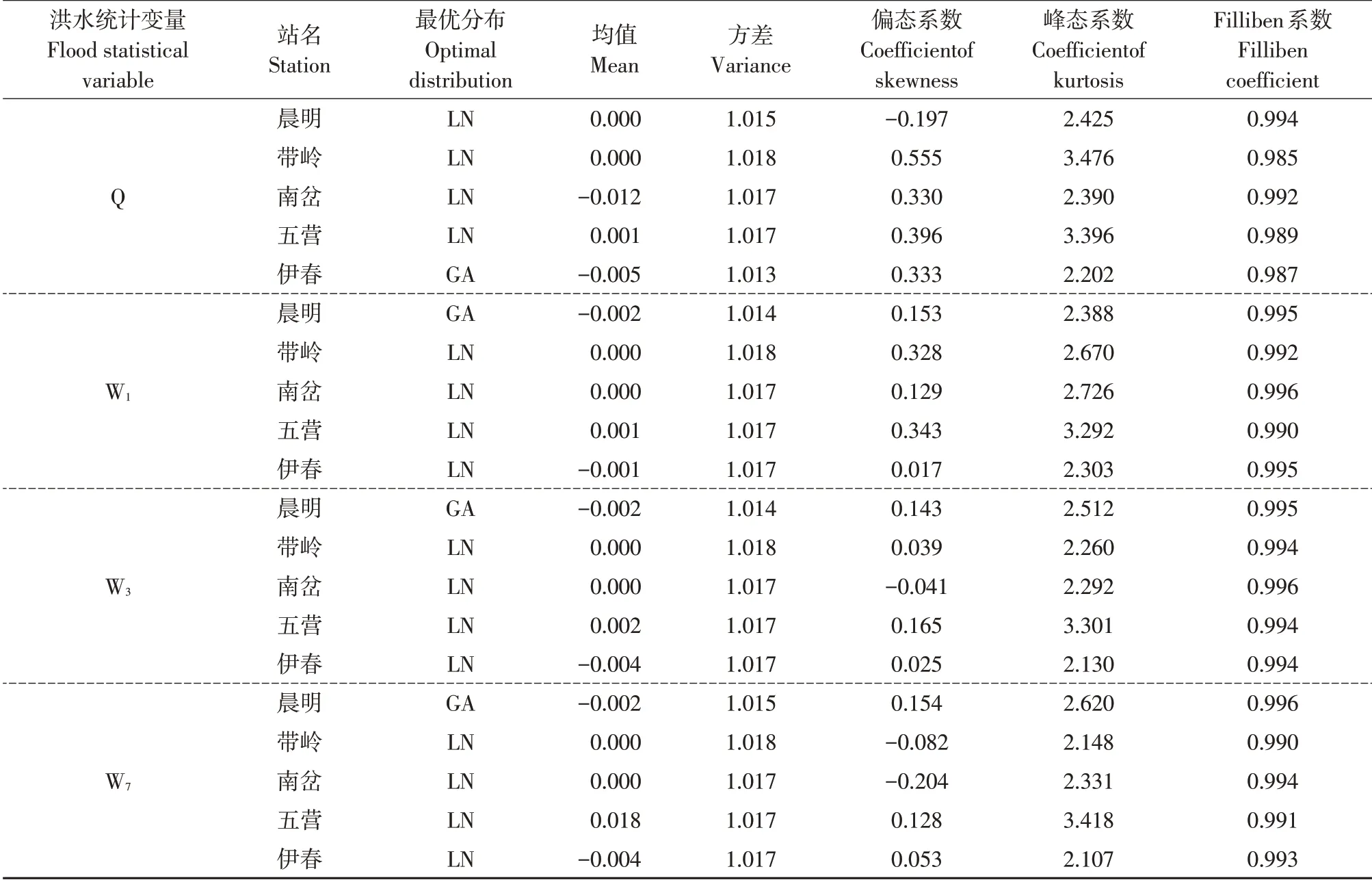
表3 时间协变量残差评价指标Table 3 Time covariate univariate residual evaluation index

以晨明站为例，图3给出各统计变量理论分布分位数与实测点据拟合结果。不同频率的分位数与相应实测点据拟合较好，各统计变量趋势变化一致，均随时间变化呈下降趋势。受历史特大洪水样本不连续性影响，分位数曲线在非连续序列时刻发生转折，使理论分位数值偏差较大，证实特大洪水对频率计算结果有影响[23]。各实测点据接近相应理论分位数，偏差均在4.5%（表4晨明站W7分位数：54.5%-50.0%=4.5%）以内。其他单站洪水理论分位数频率与实测点据频率对比情况见表4。

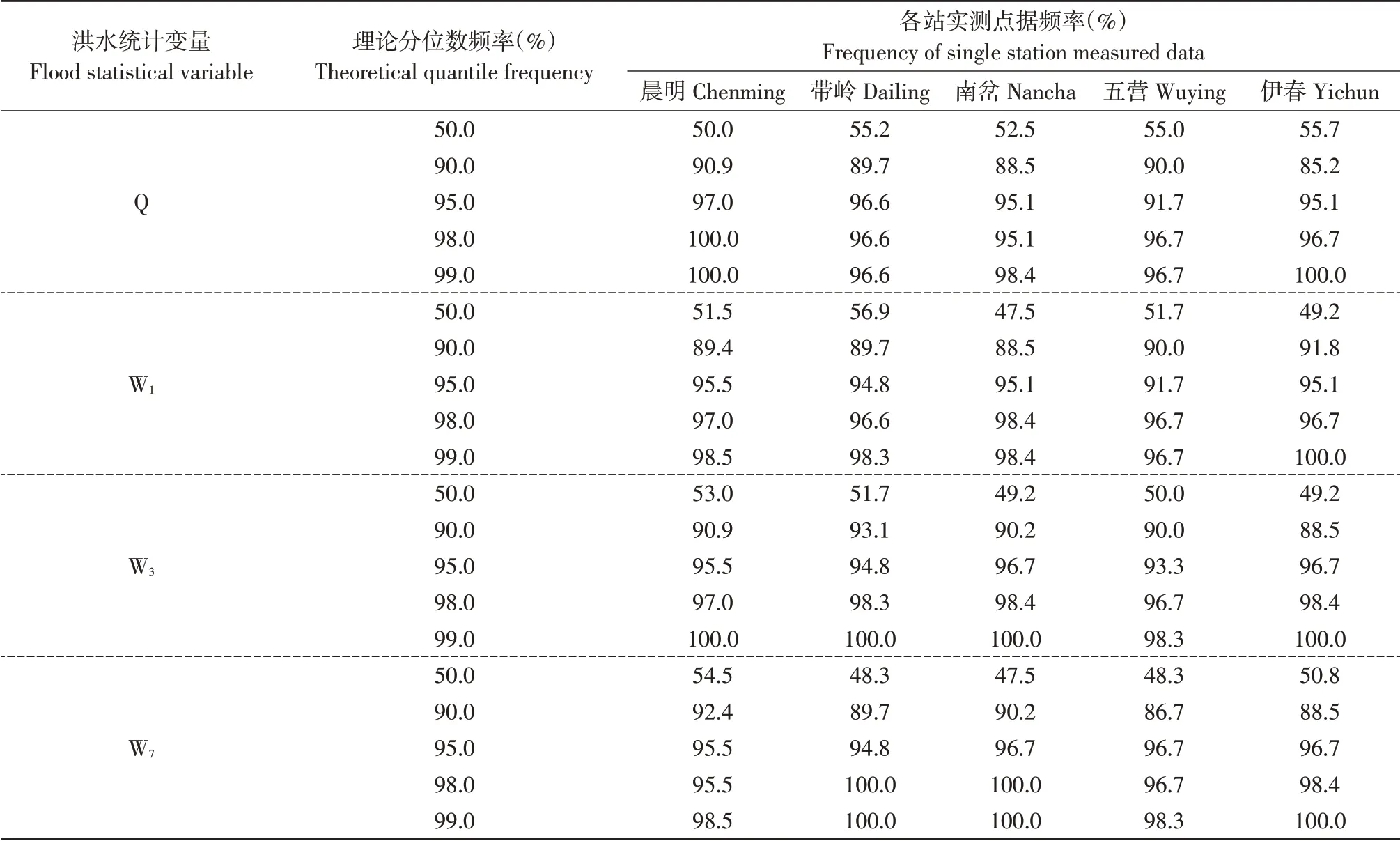
表4 理论分位数频率与实测点据频率对比（时间）Table 4 Comparison between the theoretical quantile frequency and measured frequency(Time)

图3 晨明站各统计变量理论分位数曲线图Fig.3 Theoretical quantile curve diagram of each statistical variable at Chenming Station

3.2.2 降水协变量

在洪水频率计算中，历史特大洪水作为重要计算指标，对最终设计洪水模拟效果影响较大。因此在计算某站洪水序列最优分布时，往往考虑历史特大洪水的影响。而在历史特大洪水条件下的特大降水，通常并无与之对应的历史调查数据，使采用降水作为协变量时得到的频率分布出现偏差。本文为考虑历史调查中晨明、伊春两站（其他3 站无历史特大洪水调查结果）的历史特大降水，采用H2o深度学习模型，选取历史特大降水影响因子，进行多元变量模型模拟预报。

3.2.2.1 降水量影响因子选取

为确定晨明站、伊春站降水影响因子，用于预测其历史特大洪水测站所对应降水量，使用Spearman 相关性检验方法，分析这两站洪水统计变量（Q、W1、W3、W7）、各气候因子与降水统计变量（R1、R3）相关性。由于汤旺河流域R1、R3均集中在6～9月，因此本研究仅选取6～9月相应气候因子指标。相关分析结果如图4 所示，由图4 可知，两站Q、W1、W3、W7与R1、R3均有较强相关性。但两站各气候因子与R1、R3相关性不一致。其中，晨明站NOI7与R1、R3相关性较强；伊春站NOI7、AO6与R3相关性较强。因此，两站各选取上述与降水统计变量相关性较强的影响因子用于降水预报。

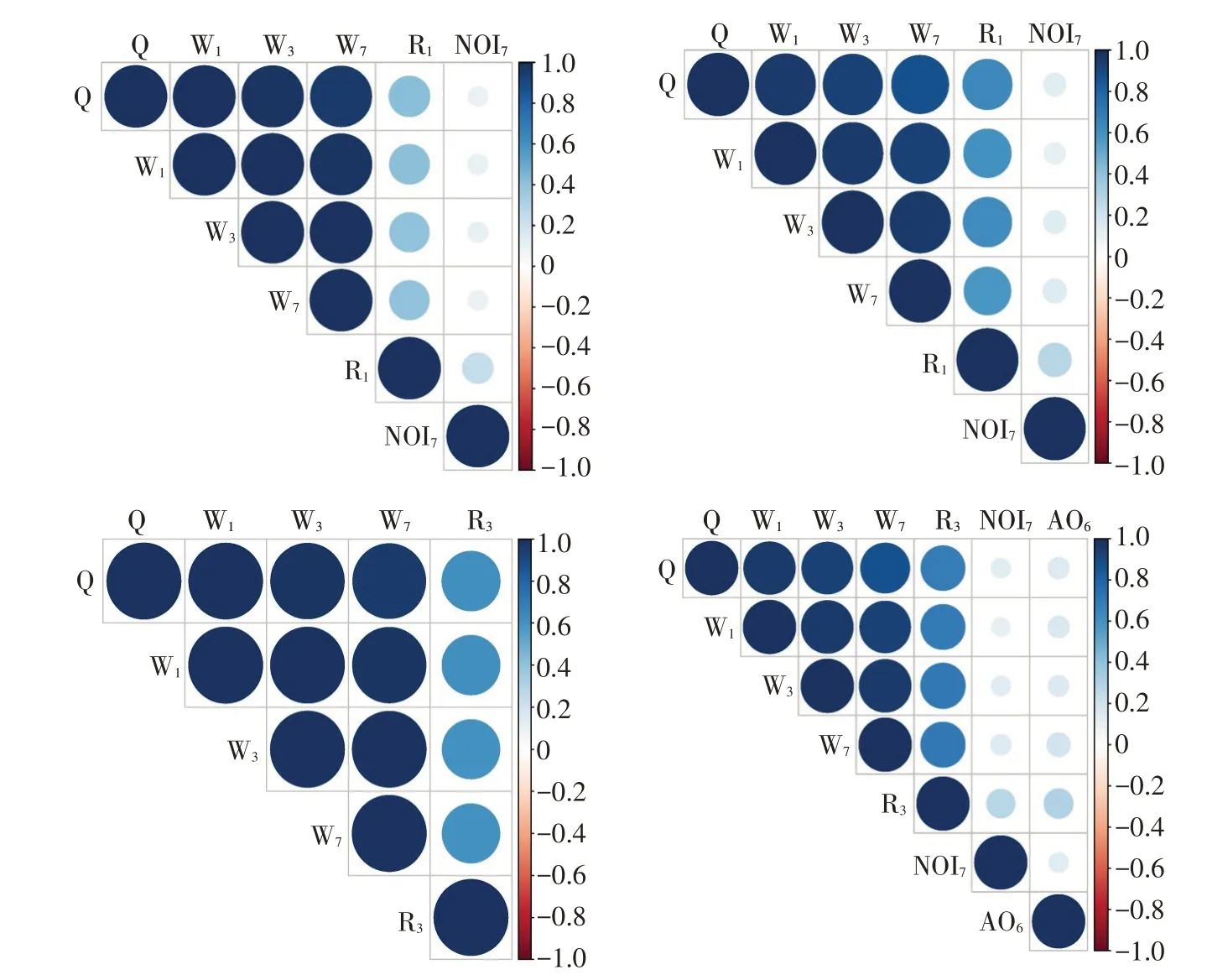
图4 晨明站和伊春站水文统计变量及气候要素统计变量相关性分析结果Fig.4 Correlation analysis results of hydrological statistical variables and climate element statistical variables at Chenming Station and Yichun Station

3.2.2.2 历史特大降水模拟

利用3.2.2.1节选取的降水影响因子，采用H2o深度学习模型分别构建晨明、伊春两站降水模拟模型，并用于历史特大降水预报。

模拟期两站降水统计变量R1、R3模拟精度如图5所示。两站不同时段年最大降水量模拟精度指标NSE、BIAS、RMSE均较优，可用于历史特大降水预报。两站历史特大降水预报结果见表5，该预报值可作为后续多变量计算中所需历史降水特大值。

表5 历史特大降水预报结果Table 5 Historical exceptional rainfall forecast results

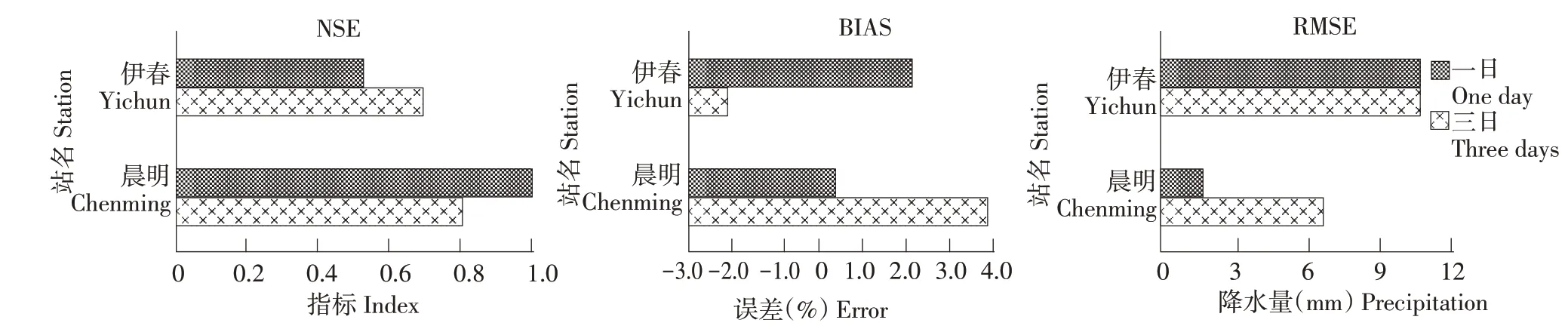
图5 NSE、BIAS、RMSE统计结果Fig.5 Statistical results of NSE,BIAS,RMSE

3.2.2.3 理论分布优选

以降水为协变量，利用AIC评价准则，选择各洪水序列最优分布。以降水为协变量的最优分布及残差评价指标结果见表6，最优分布选取除南岔站Q、W1、W3、W7和伊春站Q、W1、W7为GA，其余各站均为LN。各站残差序列均值为-0.020～0.001，方差为1.015～1.022，偏态系数为-0.278～0.560，峰态系数为2.185～4.259，Filliben 系数为0.983～0.995，该结果表明与引入时间协变量计算结果相比，各残差指标略有变化，可能是GAMLSS模型计算时以降水作为协变量而引入降水的不确定性信息（尤其是极值降水信息）所致。

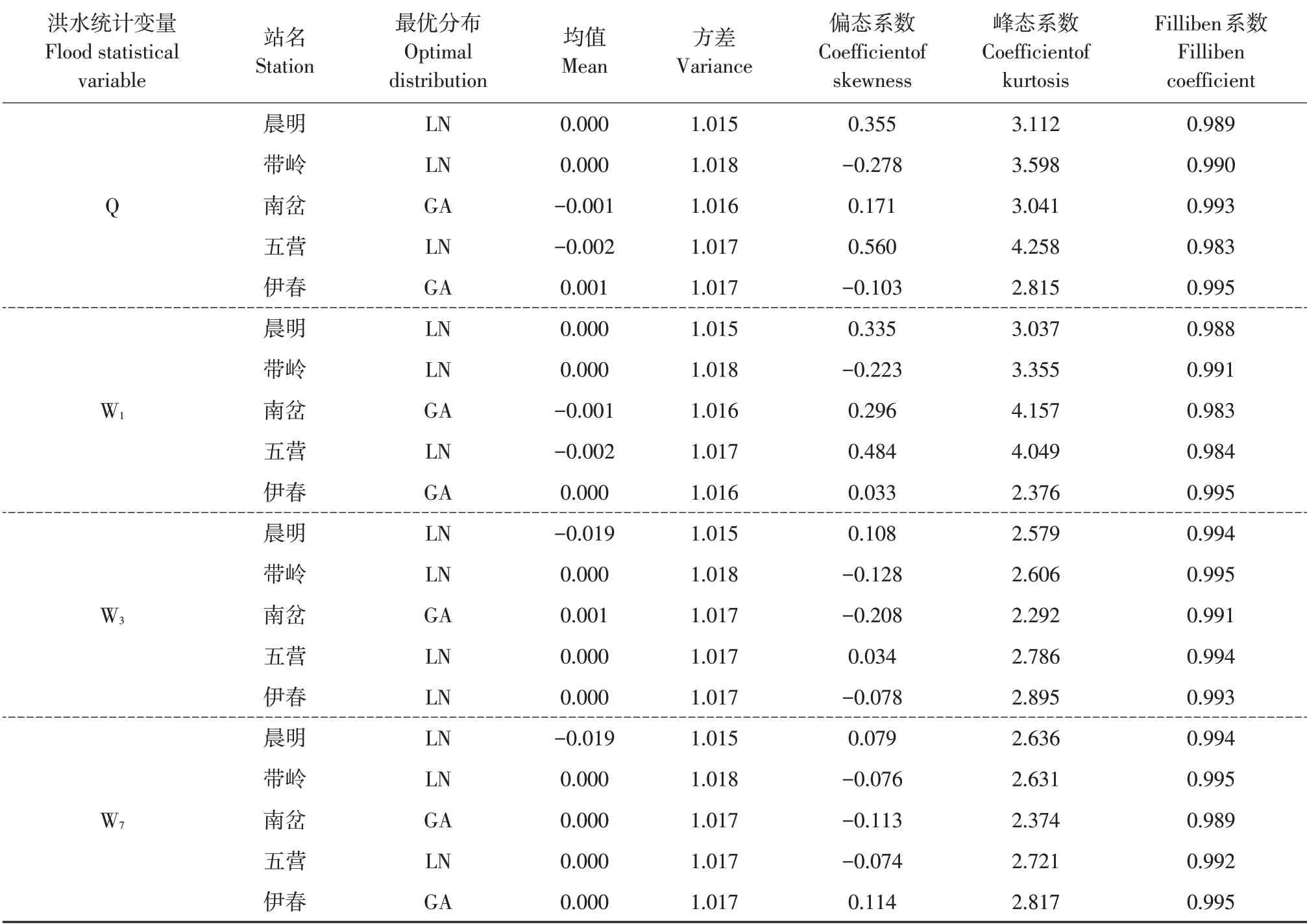
表6 降水协变量残差评价指标Table 6 Rainfall covariate univariate residual evaluation index

由于Q和W1序列是以R1为协变量，W3和W7序列是以R3为协变量，因此，得出相应分位数曲线因协变量不同而表现出不同变化特点。图6 仍以晨明站为例，给出各统计变量理论分布分位数与实测点据拟合结果。由图6 可知，Q 和W1序列分位数曲线随降水量R1增加呈先升后降趋势，且当R1达到60.0～70.0 mm 某一固定值时，拟合曲线出现极大值；而W3和W7序列分位数曲线随降水量R3增加呈先降后升趋势，当R3达到60.0～80.0 mm某一固定值时，拟合曲线出现极小值。说明考虑降水协变量使分位数曲线在某一条件下达到极值；对于R1，曲线出现极大值；对于R3，曲线出现极小值。表7 给出所有站各统计变量理论分位数频率与实测点据频率对比情况，晨明站理论分位数频率与实测点据频率偏差均在3.0%以内，偏差较小。

表7 理论分位数频率与实测点据频率对比（降水）Table 7 Comparison between the theoretical quantile frequency and measured frequency(Rainfall)

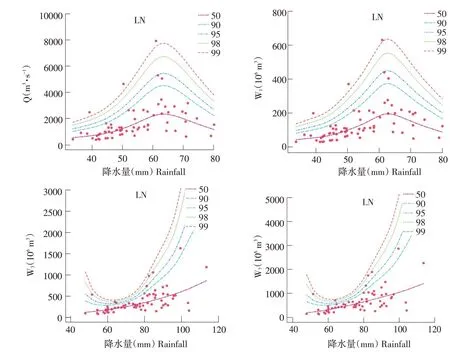
图6 晨明站各统计变量理论分位数曲线图Fig.6 Theoretical quantile curve diagram of each statistical variable at Chenming Station

4 结 论

针对汤旺河流域年最大洪峰、一日洪量、三日洪量、七日洪量，采用多变量GAMLSS模型计算不同协变量条件下洪水频率分布，得出结论如下。①基于不同条件下洪水频率分析，各站洪水统计变量最优频率曲线分布主要为GA 和LN 分布。②时间协变量加入使各站洪水统计变量最优分布类型发生变化。包含历史特大洪水的不连续序列导致理论分位曲线在特大洪水时刻曲率变化较大，应慎重选择历史特大洪水样本。③因输入的极端降水信息不确定性，使实测洪水点据与理论分位曲线拟合效果受降水影响较为明显。对于残差序列的拟合，各站残差指标评价结果与时间协变量对应计算结果不同，说明降水的加入对各站产生不同模型适用性效果。④对于非一致序列，GAMLSS模型可较好考虑时间、降水等协变量对洪水频率计算的影响，可尝试用于计算其他流域水文频率。