从问题解决“看”数学眼光的培养
孙惠惠


每一个学生的数学眼光是不同的。面对真实情景,不同数学眼光的学生提炼的数学问题不同、解决策略不同,产生的学习价值和意义也不同。数学的眼光是可以水平分层的,从知识技能、思维方式、人文素养等不同视角,审视与评价学生的相异构想,能有效提升学生的数学眼光与素养。
现实的生活是鲜活的,数学的世界是抽象的。数学的世界在很大程度上,可以被看成是我们这个真实世界高度抽象的结果。通过现实问题的真实解决,学生能从真实现象中发现数量关系与空间结构,从而提出有意义的数学问题;能从真实现象中抽象出需要研究的对象,形成数学的概念;能理解真实现象中蕴藏的数学知识,感受数学的理性美,在发展能力的同时,培养学生的数学眼光。
通过观察不同学生在同一真实问题中的不同表现,我们会深刻感受到。面对真实情景,不同数学眼光的学生提炼的数学问题不同、解决策略不同,产生的学习价值和意义也不同。同时,我们也会深刻体会到,学生所具有的数学的眼光,不仅仅是一种能力,也是一种意识,一类方法,甚至是一组综合能力。
一、从真实任务“看”问题抽象
学生的数学学习源自经验的积累和经验的不断改造。不同的知识积累,不同的生活阅历,不同的参与问题解决的已有经验,都会使得学生看待新问题的视角有所不同。这种不同和差异,带有明显的个人学习偏好和个性倾向。
(一)任务呈现
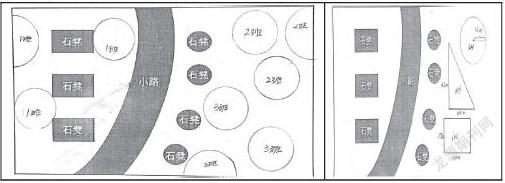
三个班级要在校园里开辟种植园地,学生们希望每一个班级分得的园地面积相等,该如何分(见下图)?
这个种植园地中有一条宽度相等的弧形小道,三条大小相等的长方形石凳和四个大小相等的圆形石凳。学生需要完成的任务是设计出三个面积相等的种植区域。面对这样的任务要求,学生在解读信息后,不同的人会形成不同的关注视角和问题解决思路。
(二)问题抽象
学生A的关注点聚焦在“面积等分”。思考的方向是如何通过计算,把可以用于种植的面积计算出来,然后再三等分,以使得每个班级分得的面积相等。学生通过测量种植区域中种植园、小路、石凳的长、宽、直径等数据获取计算所需,通过计算得到每个班级的种植面积,从而有效解决问题。
学生B的关注点聚焦在“三块面积相等的园地”。思考的方向是怎么能在空地上得到三块一样大小的面积?形状是否要相同?每班只能分一块地还是可以多块组合?如每个班级分到2.5个大小相同的圆形花坛,或者是每个班分到一个面积相同但形状不同的种植区域。
学生C的关注点聚焦在“平均分”的方法。园子中的种植面积有大有小,数据又不清楚,用怎樣的方法才能快速有效的平均分?有哪些已有的问题解决经验可以迁移使用。是化繁为简、移多补少还是面积单位分组构建,哪一种能灵活巧妙、创造性的解决问题。
从以上的问题中我们可以发现,面对同一个任务情境,不同的学生,从中抽象出的数学问题也是不同的。部分学生在面对问题时会提出与计算相关的问题,因为数字是具体可计算的,是学生最擅长使用的方法;部分学生会提出近期刚学习使用过的策略方法,如用相同面积单位个数去解决问题;还有一部分学生会借鉴前期解决与此类似或相关问题的经验,迁移方法进行尝试。这种种不同就是由数学眼光的不同而造成的结果差异。
二、从相异构想“看”问题解决
著名数学数学家丘成桐曾说过“相对于巧妙技巧来说,数学家更需要的是勤奋、眼光和思想”。面向真实的数学问题解决,静止的数字、孤立的公式能解决直观且显而易见的问题;但抽象、推理、想象,迁移、整合、创造等方法的综合运用,能更好地解决隐性、挑战、开放类的问题。
如采用“平均分”思路解决问题的学生,他们在前期的问题解决方式基本相同,都是先通过测量种植的宽,将种植横向三等分,同时等分的还有三条石凳和弧形小道。不能直接解决的问题是如何处理四个圆形石凳的问题。面对这样的问题,学生们有以下几种解决方法。
(一)区域板块面积的“移多补少”
学生1:按照横向三等分划分,2班和3班会比1班多分到半条石凳,因此,1班的种植面积就比这两个班多。
直接解决问题的方案是,把1班的种植面积分割一点给这两个班级。但是1班和3班没有直接相连的土地,因此学生采用的方案是计算出两个班需要割补的总面积,然后从1班割去总面积,2班在得到补充面积之后,再割出一般补给3班。在这个移多补少的问题解决过程中,不仅让学生感受到思想方法和计算都是问题解决的工具之一,更充分发展了学生的空间想象能力。
(二)四个石凳的“问题重述”
学生2:横向三等分划分后,4个圆形石凳横跨三个区域,因此,“种植面积等分”的问题可以重述为“4个圆形石凳三等分”的问题。
为了完美的实现平均分,学生先从量上考虑,四个圆形石凳三等分,每个班级将分到三分之四个石凳;学生还从操作性中做出考虑,怎样三等分石凳才能使之和种植区域的分割线更好衔接,并且在草图中给出了圆凳的分割示意。通过这样的问题重述化繁为简,学生不仅学会了在纷繁复杂的信息中用数学的眼光重新审视信息和重述问题,发现关键信息,更发展了学生的转化思想。
(三)一组面积单位的“分组建构”
学生:由于横向分割依然不能完全解决三等分的问题,因此,学生提出了按照不同区域分别三等分的设计思路。
学生们首先根据种植园地的布局特点划分出大小区域,按照从大到小的顺序有序思考,把能等分的区域先三等分;剩下不能等分的不规则区域后,选择更小的面积单位继续等分,直至把所有的可种植面积都分割完成。在这一过程中,学生充分利用化整为零的思想,灵活运用面积单位,化解了不规则图形面积的计算问题和等分问题。
由以上三组学生的作品对比可知,用不同的眼光去看问题,解决的过程也是截然不同的。在这一过程中,学生不仅感受到数学的数字、计算、公式是有用的,同时也能发现数学思维方式、方法迁移是有趣的、更具探索价值的。学生会感受到,数学不仅仅一种计算工具,还能在探索数学的过程中获得智力的乐趣,方法运用的美妙、问题解决的成就,让学习的过程闪烁智慧的光芒。
三、从三项评价“看”素养培养
每个学生在成长中都会遇到很多的问题。有些问题来自书本,运用已经学过的数学知识、公式、模型就能轻松解决。有些问题来自生活,没有先例可以借鉴,也不能直接运用经验解决,面对这种挑战性的问题,不同学生会有截然不同的问题解决表现。因此,如何通过评价来提升学生用数学的眼光看世界的能力就尤为重要,主要可以从以下三个维度建立评价方案。
(一)从知识的习得状态评能力强弱
不同知识水平的人解决同一个问题,评价的标准是不一样的。评价前需要分析所运用到的知识是已经学过的,还是超过自身年龄段的超前的知识,前者是知识学习后的应用,后者是知识默会后的迁移。如二年级用未学习面积单位之前,能想到不同大小区域用不同大小方块去分,值得评价为能力强;三年级学习这一知识点后采用同一方法,就只能评价为灵活应用、能力合格。
(二)从问题解决的过程方法评思维高低
不同的问题解决策略能反映出一个人的思维习惯和思维水平。面对真实问题时,有些可以运用数学知识直接解决,有些则需要运用间接经验去解决。如不能直接解决种植面积三等分的问题,是否可以转为解决四个圆石凳三等分的问题,是否可以转为化整为零的问题等等。
(三)从成果作品的人文艺术评综合素养
面对真实情境所产生的问题解决方案,最终要回归生活评价成果的实用性和艺术性。品鉴所设计的方案,是否在保留数学结构的基础上,具备了审美和艺术性,如多个种植规划方案中哪一个更美观、更具实用性;剖析学生用作品表达想法时,图形表达、色块区分是否具表现力;观察作品发布会的公开展示中,分享、展示、团队合作是否熟练、有效,是否能更多的获得同伴与他人的认可与赞赏等。
数学眼光的培养是贯穿一个学生一生成长的重要素养。数学眼光的培养不仅仅知识为了强调一个知识点,更重要的是在改变学生的一种观察视角与思维方式,重塑看待问题的眼光。从孤立的、静止地看待一个数学问题,到会主动使用动态、发展的眼光来理解数学与生活,不断提升个体跳出认知的局限的实力,发展解决问题的综合能力。DDC37891-CE87-47D1-9684-E3D4034F4D14

