教材对比中揣摩编者意图

是菲菁

[摘 要]分数是小学阶段公认的教学难点。文章将苏教版和人教版教材的分数内容进行对比，根据其中的区别和联系，分析教材的编写意图，得出分数教学的基本原则和有效方法，从而提高教学效率。

[关键词]人教版教材;苏教版教材;分数

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）08-0023-03

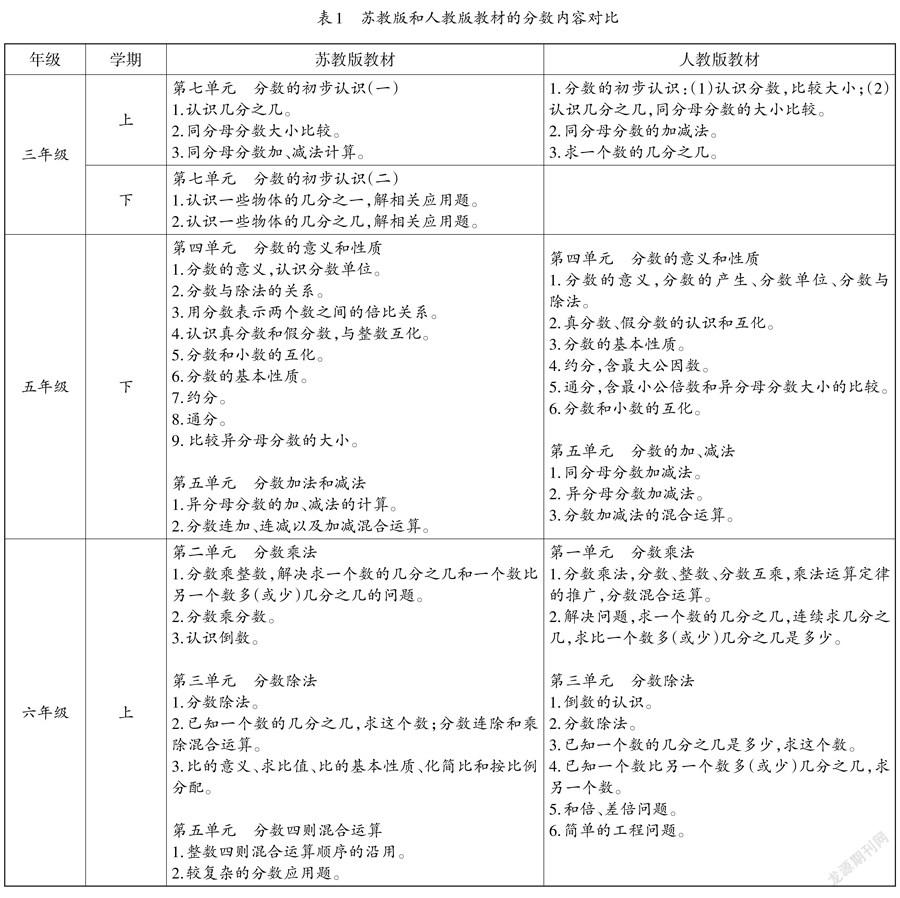
分数课程主要分为四大块：一是概念，主要包含分数的基本意义、分数单位的定义、分数的读写规则、分数的分类等内容;二是分数的相关计算，主要是分数的基本运算法则，包括四则混合运算和简算;三是分数的应用，也就是分数在生活中的应用;四是分数知识的综合应用。本文将苏教版和人教版的分数内容（如表1）进行对比，发现有以下异同点。

一、难易顺序相似

两个版本教材均是按照由易到难、由浅入深的原则编写的，以分数为主阵地，适当融入其他知识：（1）前置和分散难点，梯度性安排知识。从表1可以看出，两个版本教材将分数意义“打散”，提前做出嵌入式和分段式的设计。两个版本教材都是在三年级就开始编排分数知识，尤其是苏教版教材，将由一个物体得到的分数和由一个整体得到的分数分设在上、下两个学期，为渗透分数的意义和单位“1”做好部署。（2）根据学情调整内容，在分数与除法之间搭建桥梁。学生在第三学期接触除法时，知道什么是等分除，以及商一般为整数。对此，两个版本教材都运用知识迁移，以平分物品为背景，让学生经历不能彻底平均分，也就是商无法取整，从而引发学生的认知冲突，顺理成章地引入分数。两个版本教材重点突出分数与除法的联系，将本应于六年级学习的“求一个数的几分之几是多少”大大提前，教将其紧随“认识分数”之后。图1是苏教版教材第六册第83页的教学内容：

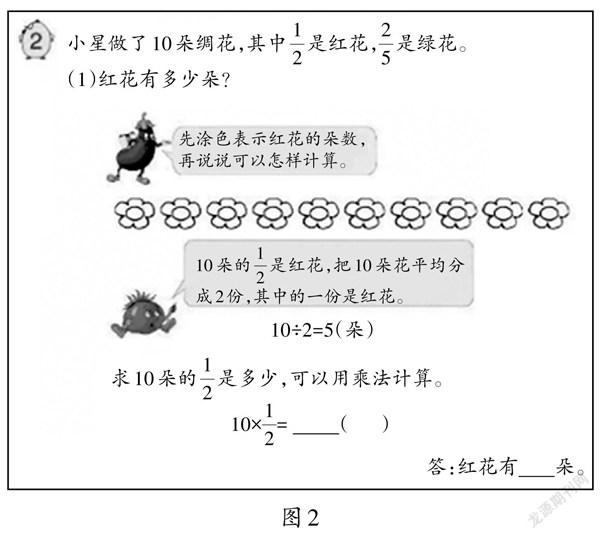
如此安排，一方面让学生用等分除的意义来解决平分物品的问题，勾连除法与分数的关系，并在解题过程中渗透和深化几分之几的意义，为推出单位“1”造势;另一方面，利用除法解决六年级的分数问题，抓紧时机渗透分数的第二重意义，既减轻了学生六年级的学习负担，又增厚了三年级的分数的知识底蕴，也有助于学生理解分数乘法的意义（如图2，苏教版教材第十一册“分数乘法”的例2），进而掌握算法。

分数是一个系列性的知识，在小学阶段占有很大比重，而且与其他知识（如除法、比例、小数等）存在很多交集，因此它的教學顺序尤为重要。既要考虑到分数本身的知识序列，又要兼顾到分数与其他知识的平稳对接，比如对“单位1”的渗透就是一大难点，分次渗透比一次性渗透要好。学生最开始学习的分数内容，是分数的基本意义——将一个物体平分成若干份，取其中一份或者几份的数，用分数表示。这是为了给学生建立最小单位可以“切分”的观念，如把一个苹果平分成3份，原来是不可分的，现在可以将苹果“切开”，于是出现了分数。后来的将多个物品组成的集合看成是“单位1”则是为了与等分除对接，等分除中，当总数小于平分的份数时，如把3个苹果平分成5份，每人分得几个苹果，可以理解为每份为3个苹果的[1/5]，也就是3×[1/5]=[3/5]，甚至可以按照一般除法的思路，直接用总数（3）除以份数（5）得到[3/5]，即3÷5=[3/5]。将“求一个数是另一个数的几分之几”放到“分数除法”这一单元，也是为了把分数和将整体看成单位“1”关联起来。

二、“借助直观”方面相同

借助直观操作渗透意义和算理，掌握算法。（1）借助直观操作渗透意义和算理。在最初教学分数时，两个版本教材都是先直接出示物品分割图、创设动手切分物品的情境，然后阐释分数的意义和算理。如苏教版教材第五册第90页的例3，呈现两个小学生在画图涂色中描绘分数。（2）运用画图策略，渗透算理和算法。两个版本教材在解决分数问题时，热衷于通过画图来揭示算理，发展学生的几何直观能力。如在诠释分数乘分数的算理中，先画出长方形，通过两次画分数来表述分数相乘的现象，最后通过直观图呈现的结果来归纳算法。又如类似“连续求一个数的几分之几是多少”的分数问题，苏教版教材第十一册第35页给出了“根据题意补完线段图，思考首先算什么，为什么这样算”的提示语，并且配上线段图，让学生边画图边领会数量关系。人教版教材第十一册第13页则在提示“折纸或画图可以使思路变得直观”的基础上配了折纸示意图，以帮助学生理解。

数形结合是一种基本的数学思想，它贯穿于整个小学数学中。数本身就是一个抽象的理论，从结绳记事开始，数字的出现就带有物品计数的特征，低年级的数数，都是从对常见物品的累计开始的。学生从一个个物品（如苹果、鸭子）中抽象出整数，但直观操作对简易运算的学习具有深远影响，学生在此时已经形成丰富的经验和路径依赖。分数是比整数更加抽象的数型，分数的学习和理解需要继承之前的直观学习法。因此，先用平分物品（单位“1”）的方法构建分数，再用平分几何图形的方法来演示分数运算的算理，就能将分数的意义和运算原理剖析得淋漓尽致，而且这种方法与几何直观完美融合。后续的求一个数是另一个数的几分之几，需要对单位“1”做重新解读（将后者标准量看作是单位“1”）时，采用线段图就能更好地显示前者占后者的比例（利用线段的单位长度来对比）。不同的内容采用不同的几何直观素材，贴切得体。

三、内容先后各异

约分、通分与因数、倍数等内容的出场顺序不同。分数的基本性质是分数的一个重要知识点，直接关系到因数、倍数的学习和运用，直至后面的约分和通分，可谓涉及很多知识。两个版本教材在这一连串知识的编排顺序上大相径庭。苏教版教材是在第十册第3单元单设“因数与倍数”一章，将因数和倍数的概念全部推出，在紧随其后的第4单元安排分数的意义和性质，在第5单元安排分数的加减法，前后逻辑缜密、严丝合缝。人教版教材则在第十册第2、第4、第6单元间隔安排了同一内容，断断续续，且第2单元虽然也安排了“因数和倍数”，但是却把公因数、最大公因数和公倍数、最小公倍数等其他子概念安排在第4单元，与约分、通分交织在一起，相比之下，人教版教材的安排稍逊一筹，显得零零散散。

其实，从某种程度上说，学习因数和倍数的目的是为通分和约分服务，通分和约分又是为分数的运算服务，这其中最基础的理论就是分数的基本性质，约分和通分都是以分数的基本性质为理论依据的，约分需要用到公因数（最大）概念，通分需要用到公倍数（最小）概念，于是，因数和倍数就成了最基础的部分。因此，应该将这所有的内容安排到一个版块，一气呵成，而不应该分散教学，要与前面所有和分数有关的直观学习法“抱团”形成合力，打造培养学生数形结合思想的摇篮。

四、归属与风格不同

倒数的认识和比的单元归属不同。倒数起源于分数乘法，但是却在分数除法中“发扬光大”。苏教版教材循旧例，将“倒数的认识”安排在“分数乘法”后;人教版教材则把“倒数的认识”作为“分数除法”的引言。分数和比密切相关，人教版教材循旧例在“分数除法”之后单设“比”这章节，在这个单元中沟通比与分数之间的联系;苏教版教材则把“比”渗透到“分数除法”单元中，作为拓展内容讲述。比较两个版本教材的处理方式，前后联系都较为紧密，不分伯仲。

分数应用题选题风格和解题过程差异大。两个版本教材都是将解决简单的分数问题融入分数乘除法中，让学生边解决问题边学会计算。人教版教材在第十一册“分数除法”单元重提和倍、差倍，以及工程问题和小数分数混合相乘问题，恰到好处地渗透了方程思想和假设思想，尤其是简单的工程问题，不仅渗透了假设法，还提倡解题方法的多样化。小数乘分数的计算，是为了在解决问题中培养学生思维的灵活性和数形互化的意识。比较解题过程后发现：人教版教材的“阅读与理解”“分析与解答”“回顾与反思”的提示明确直白，在“阅读与理解”环节培养学生的读题能力，在“分析与解答”环节落实逻辑推理，在“回顾与反思”环节梳理解题流程和步骤，进而培养学生自主学习的好习惯。苏教版教材则是利用小卡片提示语提点学生，解答过程主张“填空”，弱化读题能力的培养。虽然苏教版教材“回顾与反思”环节的内容不多，但“小卡片”总结很到位，如分数四则混合运算中的例2，多张卡片提示非常翔实，分析、解答、反思的过程细致，详略得当。

人教版和苏教版教材在分数相关内容的编排上各有千秋，只有详细研究，摸透编者的编写意图，才能归纳出有效的教学方法，实现高效教学。

（责编 金 铃）