区域限制及人工势场引导的改进RRT路径规划算法

徐劲力，曹 其

(武汉理工大学 机电工程学院，湖北 武汉 430070)

路径规划是指从起始位置到目标位置生成一条无碰撞路径，在无人驾驶、手术医疗、航空航天[1-3]等多个领域都有广泛应用。到目前为止，根据采用的类型方法，常用的路径规划算法有图搜索法[4-5]、随机采样法[6]、人工势场法[7]和智能算法[8]等。其中人工势场法算法简单且容易实现，同时所规划的路径平滑，但容易陷入局部极小值。快速探索随机树(rapidly-exploring random trees, RRT)算法避免了空间建模，能够高效解决高维空间和复杂约束的路径规划问题，但由于该方法在生成扩展树时在整个采样空间内随机采样，因此扩展会过于平均，整个算法的效率较低。蚁群算法、神经网络法等智能算法应用于复杂环境时需要大量迭代去寻找并优化路径，因此求解困难、收敛时间长。

为了提高搜索速度，Karaman等[9]提出了渐进最优RRT算法(RRT*)。针对RRT算法的采样生成点盲目性强的缺点，Bruce等[10]将启发思想融入RRT算法形成了Informed RRT*算法，该算法建立一个长轴上的焦点位于起始点和目标点的椭圆区域，在该区域进行随机点采样，并在路径搜索过程中不断调整椭圆区域，以提高随机采样点可用概率。为了利用环境信息引导随机树生长，很多学者研究了RRT算法与人工势场法的结合。文献[11-12]在人工势场法陷入局部最小值时，利用RRT算法的随机性选择临时目标点，以此跳出局部极小值点；文献[13]先采用RRT进行全局路径规划，再使用人工势场法进行局部避障；文献[14]采用人工势场法优化RRT*的采样过程，减少了算法的计算量。

笔者在现有研究基础上，针对现有的RRT算法随机性强、没有偏向性以及采样空间密集等问题，提出区域限制及人工势场引导的改进RRT路径规划算法(AL-APFG RRT —— Goal_bias RRT with area limitation and guided by artificial potential field)。算法通过在采样开始前根据起始位置与目标位置，规划包含起始点与目标点的有界连通区域，并根据循环次数调整采样区域；在规划过程中根据节点与障碍物的相对关系自适应调整选择目标点作为随机点的概率P，在人工势场法引导下，规划出一条无碰撞的路径。

1 传统算法

1.1 RRT算法

RRT的思想是快速扩张一群像树一样的路径以探索空间的大部分区域，伺机找到可行的路径。将起始点作为根节点，从根节点开始生长枝丫；在机器人的构型空间中，生成一个随机点；在树上找到距离随机点最近的那个点，朝着最近点到随机点的方向生长，如果没有碰到障碍物就把生长后的树枝和端点添加到树上，直至目标点也添加到树上，最终找到一条连接起始点与目标点的完整路径。经典的RRT算法是完全随机的，搜索过程也没有偏向性，因此效率比较低。

Goal_bias RRT在RRT算法的基础上，添加了以一定的概率P选择目标点作为随机点的概率，当随机数小于P时，选择目标点作为随机点，进行碰撞检测和生长；当随机数大于等于P时，在地图范围内生成随机点。从而引导随机树在一定程度上向目标点生长。

1.2 人工势场法

人工势场法是一种将物理学中场的概念引入到路径规划中的算法，是应用最广泛的机器人路径规划算法之一。人工势场法的基本思想是把机器人在环境中的运动视为一种在虚拟力场中的运动，将机器人假设成一个点，虚拟力场由目标点对机器人的引力场和障碍物对机器人的斥力场组成。引力场由目标点产生，斥力场是由所有的障碍物产生的合力场组成。因此，人工势场法的势场函数定义为引力场与斥力场的势场和，如式(1)所示。

U(q)=Uatt(q)+Urep(q)

(1)

式中:q为机器人位置节点；Uatt(q)为引力势场函数；Urep(q)为斥力势场函数；U(q)为势场函数和。

其中，引力势场函数为：

(2)

式中：Katt为引力常数;qgoal为目标节点。

斥力势场函数为：

(3)

式中：Krep为斥力常数；ρ0为障碍物影响距离；ρobs(q)为机器人位置节点q指向距离最近的障碍物的向量。

引力函数为：

Fatt(q)=-Katt(q-qgoal)

(4)

斥力函数为：

(5)

2 改进算法

2.1 新节点的生成

Goal_bias RRT算法以一定概率选择目标点作为随机点，在一定程度上使算法具有了偏向目标点生长的能力，提高了搜索效率。但在搜索过程中，没有考虑到路径规划环境的影响，因此采用人工势场法的思想，将引力势场和斥力势场引入随机树的节点生长过程中，合理利用目标点及附近障碍物的信息，计算最近点qnear处所受的引力和斥力，结合所生成的随机点，共同决定生长方向。大多数RRT算法采用等步长扩展的方法，不容易通过狭窄区域。笔者采用了限制最大步长的方法，使距离超过最大步长的统一按照最大步长扩展，距离小于最大步长的，则直接按照随机分量和势场合力分量共同作用扩展，使随机树容易通过狭窄区域，并远离障碍物，偏向目标点生长。

新节点qnew的生成过程如图1所示，其计算公式如式(6)所示。

图1 新节点生成过程

(6)

式中：F为机器人在qnear处所受的合力；λ为最大步长；ε为势场力分量因子，取(0,1)之间的数，通过调整ε的大小可以调整势场对新节点生成方向的影响；qrand为随机点。

2.2 自适应概率采样

Goal_bias RRT按照一定概率选取目标点作为随机点，一定程度上引导随机树向着目标点生长，同时还有优先生长一条分支的特性，有利于快速规划出一条可行路径。但是由于Goal_bias RRT算法中选择目标点作为随机点的概率p是一个固定值，使得在障碍物环境复杂或狭窄区域时，选取目标点为随机点往往是无效的。因此笔者提出了一种根据树上节点与障碍物环境的相对关系，自适应的调节概率p的方法。

当最近点qnear附近有障碍物时，减小选择目标点作为随机点的概率p，以便尽快绕开障碍物。当目标点qgoal附近有障碍物时，如果选择目标点作为随机点，不容易扩展新节点，因此容易陷入局部极小值，为了减少这种情况，也减小选择目标点作为随机点的概率p。概率的获得方法如下：

(7)

式中：pmax为最大概率；ρq2obs为节点到最近障碍物的距离；ρgoal2obs为目标点到最近障碍物的距离。

2.3 区域限制

为了减少计算量和过多的搜索空间，增强计算效率，在算法开始采样前，在配置空间Z中确定一个包含起始位置和目标位置的连通区域，如图2所示，该连通区域以起始点A与目标点B的连线为角平分线。起始搜索区域的角度为30°，如图2(a)所示。随着搜索次数的增加，连线AC与AD分别沿逆时针方向与顺时针方向旋转一定的角度(15°)以此扩大采样区域，直到生成全局路径或者将区域逐步扩展到全图，如图2(b)所示，在区域扩展为210°时找到一条可行路径。

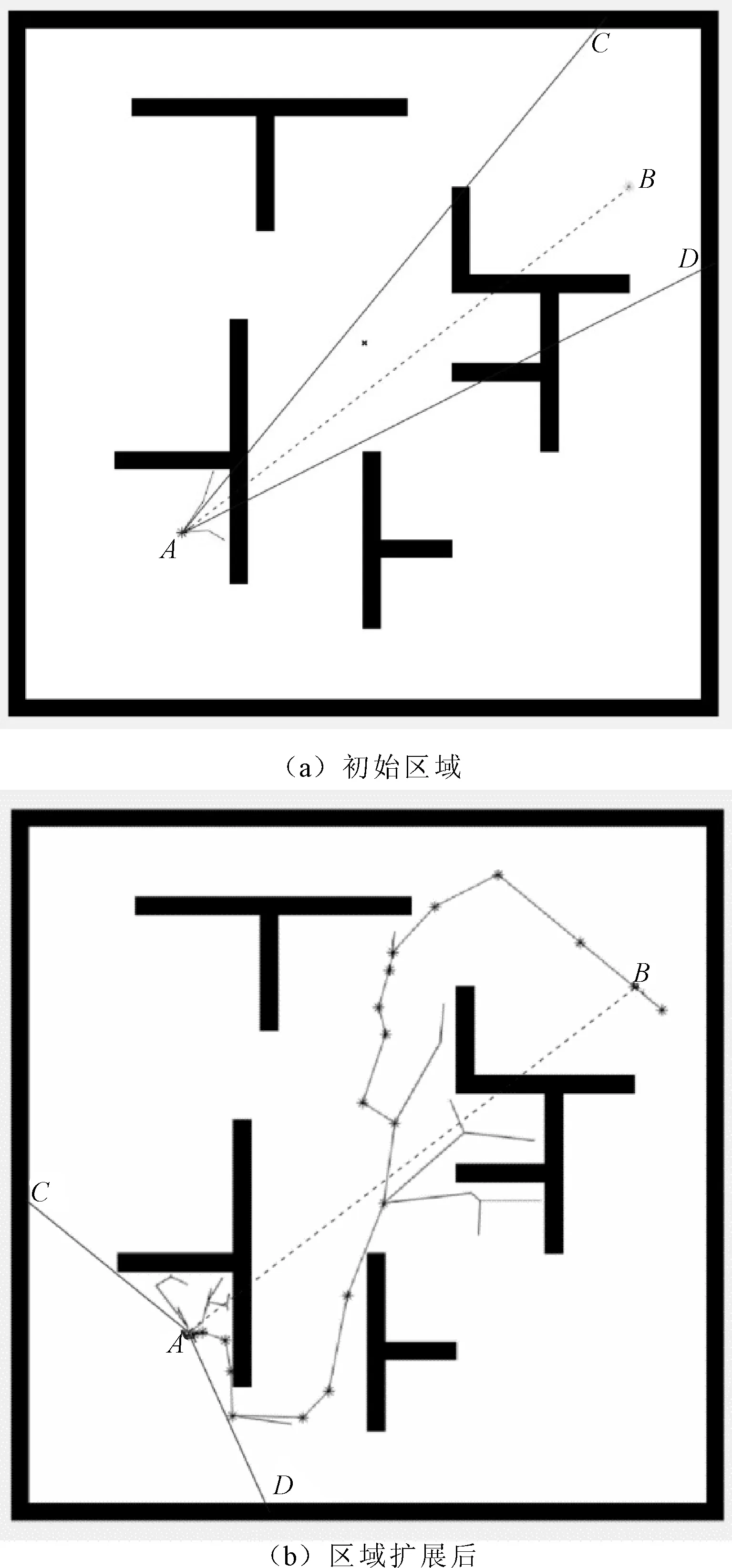
图2 采样区域的扩展

3 仿真分析

为了验证所提出的算法AL_APFG RRT 的有效性和收敛速度，在MATLAB 2018a中进行了多组对比实验。仿真在联想小新V3000(CPU：Intel Core i7-5500U(2.4 GHz/L3 4 M)；内存：8 GB DDR3L 1600；硬盘：500 GB HDD，8 GB；显卡：AMD Radeon R5 M230独立显卡)上进行。在仿真环境中的参数设置如表1所示。对基本RRT算法、Goal_bias RRT 算法、人工势场引导的Goal_bias RRT算法(APFGRRT)[14]和AL_APFG RRT 算法进行仿真，给出4种算法最终生成的随机树和连接节点的最终路径，对这几种算法在相同地图环境和相同参数下进行50次重复测试，取平均值作为实验结果。

表1 参数设置

图3中，x轴和y轴的坐标范围均为[1,800]，A为起始点，B为目标点，*节点轨迹是根据树上节点规划出的轨迹。图3是在一般场景下4种算法的表现。

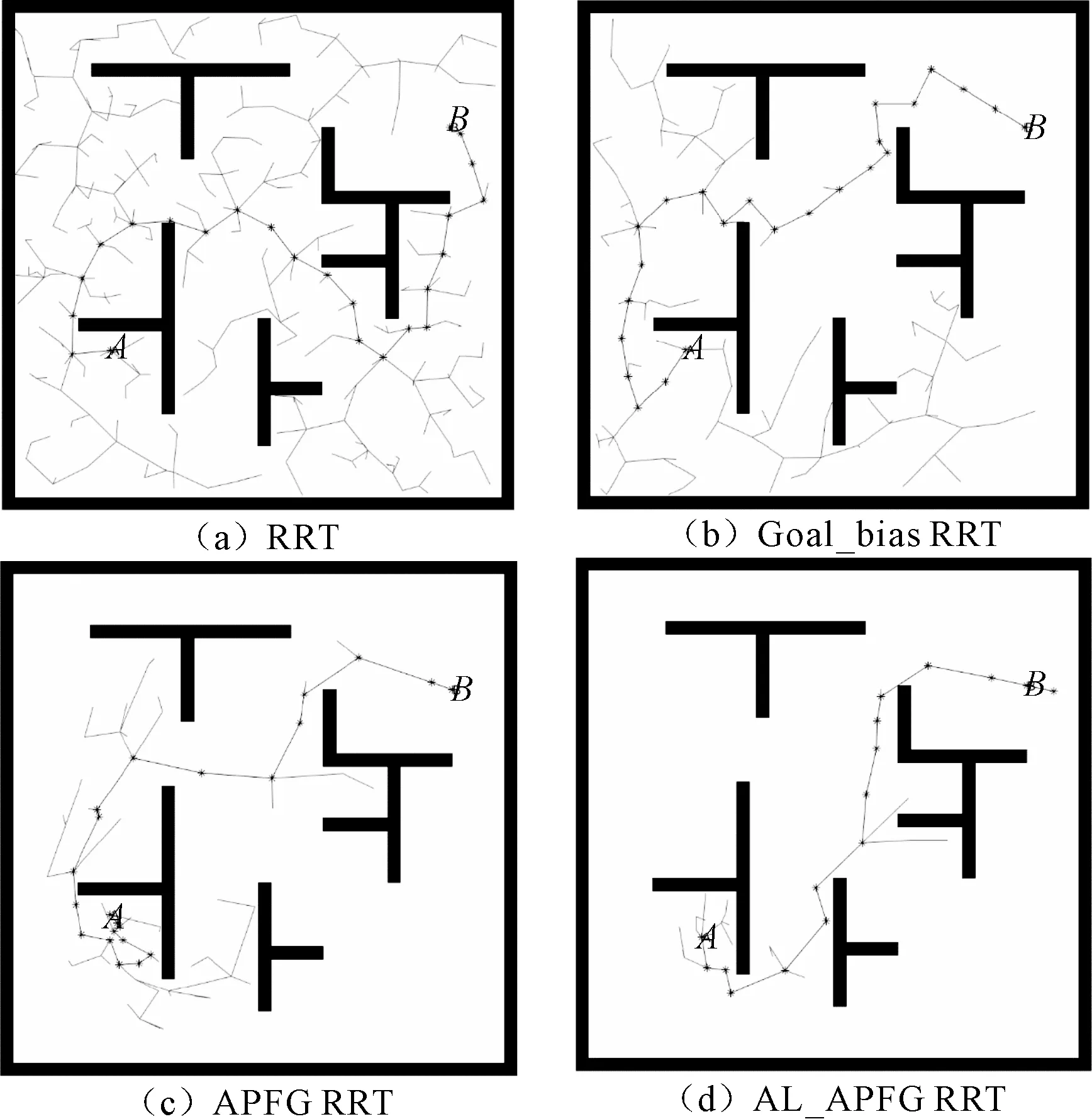
图3 4种算法在一般场景中的表现

从图3(a)可知，一般RRT算法在空间中的采样过于均匀，树上节点过多，且有很多无用节点；从图3(b)可知，Goal_bias RRT相对于基本RRT算法节点数已明显减少；从图3(c)可知，APFG RRT算法节点数进一步减少，但不容易跳出局部极小值，经过从头生成另一个分支后才寻到路径；从图3(d)可知，AL_APFG RRT算法改善了前面3种算法采样过于平均、不容易跳出局部极小值的缺点，以较少的节点数完成了路径规划。

表2为一般场景中4种算法的规划时间、节点数量和迭代次数。

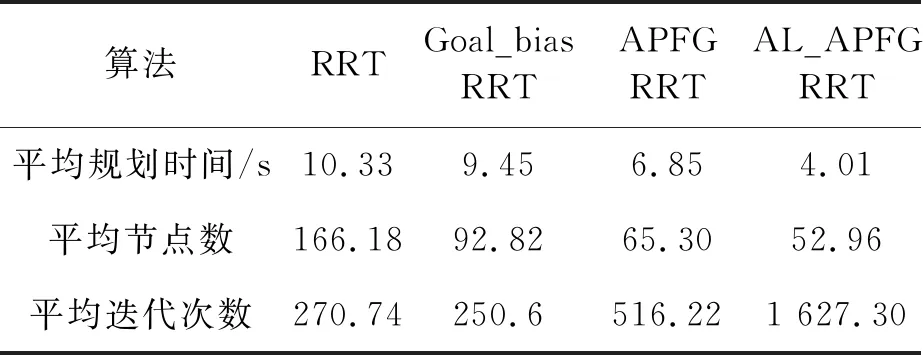
表2 4种算法在一般场景中的实验结果对比

从表2可知，笔者提出的算法在一般场景中路径规划所耗费的平均时间上相对于初始的RRT算法减少了61.17%，平均节点数减少了68.13%；相对于Goal_bias RRT算法平均耗时减少了57.56%，平均节点数减少了42.94%；相对于APFGRRT算法平均耗时减少了41.46%，平均节点数减少了18.90%。

表3为狭缝场景中4种算法的实验结果。图4为在狭缝场景下4种算法的表现。从图4可知，在狭窄场景中，AL_APFG RRT算法相对于其他3种算法更容易找到可行路径。

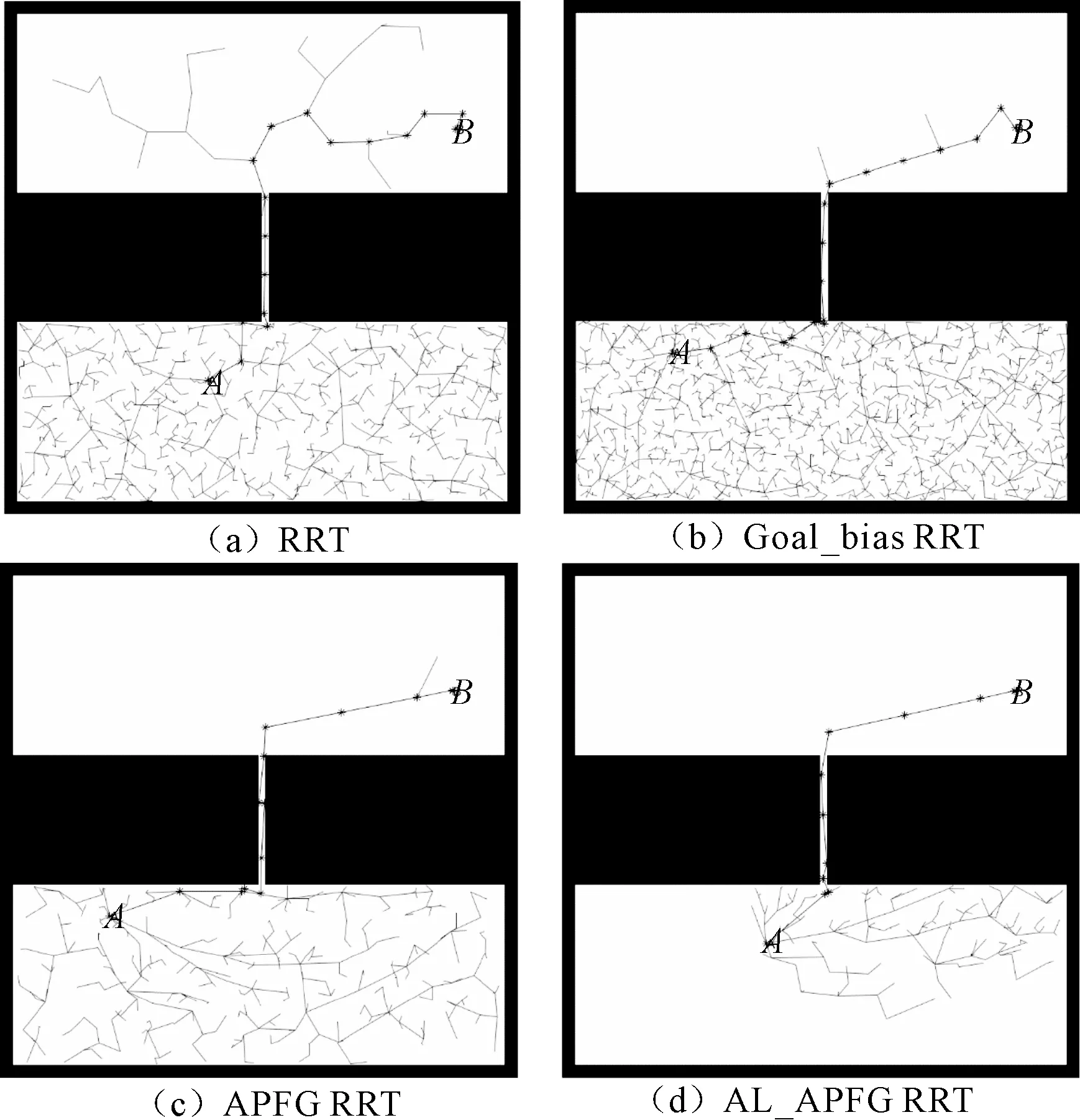
图4 4种算法在狭缝场景中的表现

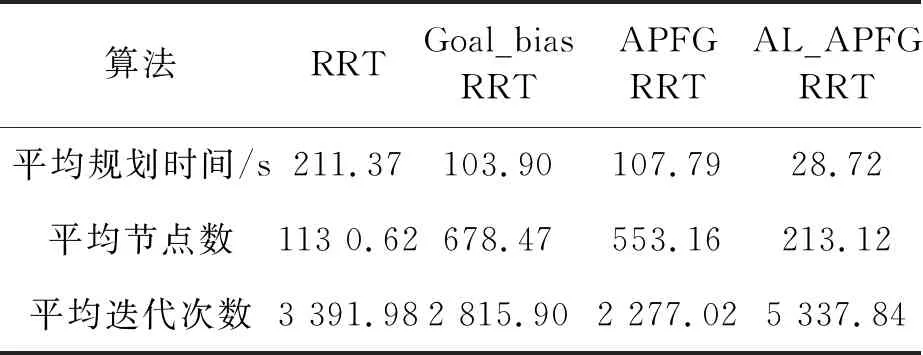
表3 4种算法在狭缝场景中的实验结果对比

从表3可知，笔者所提出的算法在狭缝场景中路径规划所耗费的平均时间上相对于初始的RRT算法减少了86.41%，平均节点数减少了81.15%；相对于Goal_bias RRT算法平均耗时减少了72.36%，平均节点数减少了68.59%；相对于APFG RRT算法平均耗时减少了73.36%，平均节点数减少了61.47%

由于人工势场的引入以及随机取样点的区域限制增加了迭代次数和计算量，导致本文算法的迭代次数有较大增加，但同时大大减少了无效节点的数量，进而提高了搜索效率。由上面的结果可知，无论是平均规划时间还是平均节点数，笔者所提出的算法均优于前面3种算法。

4 结论

笔者提出了AL_APFG RRT算法的路径规划算法，改进了RRT算法在取样区域过于平均的问题，并且在扩展新节点时充分利用了周围的环境信息，增强了算法在采样中的偏向性，路径规划的搜索效率进一步提高。仿真结果表明，该算法在一般场景和狭缝场景中耗时更短，平均节点数更少，对机器人的路径规划研究有一定的参考意义。