思维导图辅助初中数学解题教学研究

崔玉民

【摘要】本文将以思维导图为中心，首先分析现阶段思维导图在初中数学解题教学中的应用问题，最后结合例题提出相应的应用策略及措施.

【关键词】思维导图;初中数学;解题教学

1 思维导图制作过程中关键字词整理

思维导图在辅助初中数学解题教学过程中抓取和整理关键字词显得尤为重要.在复习中，引入以圆为关键字词的复习思维导图（如图1所示），然后进行题目练习，解题教学质量会事半功倍.

引入以下题目，引导学生结合思维导图解答.

如图2所示，以AB为直径的圆O分别于BC，AC相交于点D，E，BD=CD，过点D作圆O的切线交边AC于点F.

求 （1）求证：DF⊥AC;

（2）若圆半径为5，∠CDF=30°，求BD弧长（结果保留π）.

教学分析 从第一问进行分析，从关键词的抓取出发，结合题目当中的相关叙述得到条件，O，D分别位于线段AB，BC的中点，所以连接OD，OD则是△ABC的中位线，以D为切点，即能够证明;从第二问进行分析，已知∠CDF=30°，∠ODF=90°，r=5，从关键词进行联系，则可以推出△BOD为等边三角形，然后从结合弧长公式则能够得到答案.

解 （1）因为DF是圆O的切线，D为切点，

所以OD⊥DF，

所以∠ODF=90°，

因为BD=CD，OA=OB，

所以OD是△ABC的中位线，

所以OD∥AC，

所以∠CFD=∠ODF=90°，

DF⊥AC.

（2）因为∠CDF=30°，

由（1）得∠ODF=90°，

所以∠ODB=180°-∠CDF-∠ODF=60°，

因为OB=OD.

所以∠OBD=60°，

所以△BOD是等边三角形，

∠BOD=60°，

所以BD弧长为60°πR180=53π.

题目总结 根据题目所知第一问主要考查圆与三角形中位线相关的知识点，第二问主要考查弧长公式的运用，所以在解题教学之前，教师应该注重将二者运用思维导图进行连接，带领学生对此类知识点进行回顾，再开展教学.

2 丰富思维导图制作过程中个性化设计

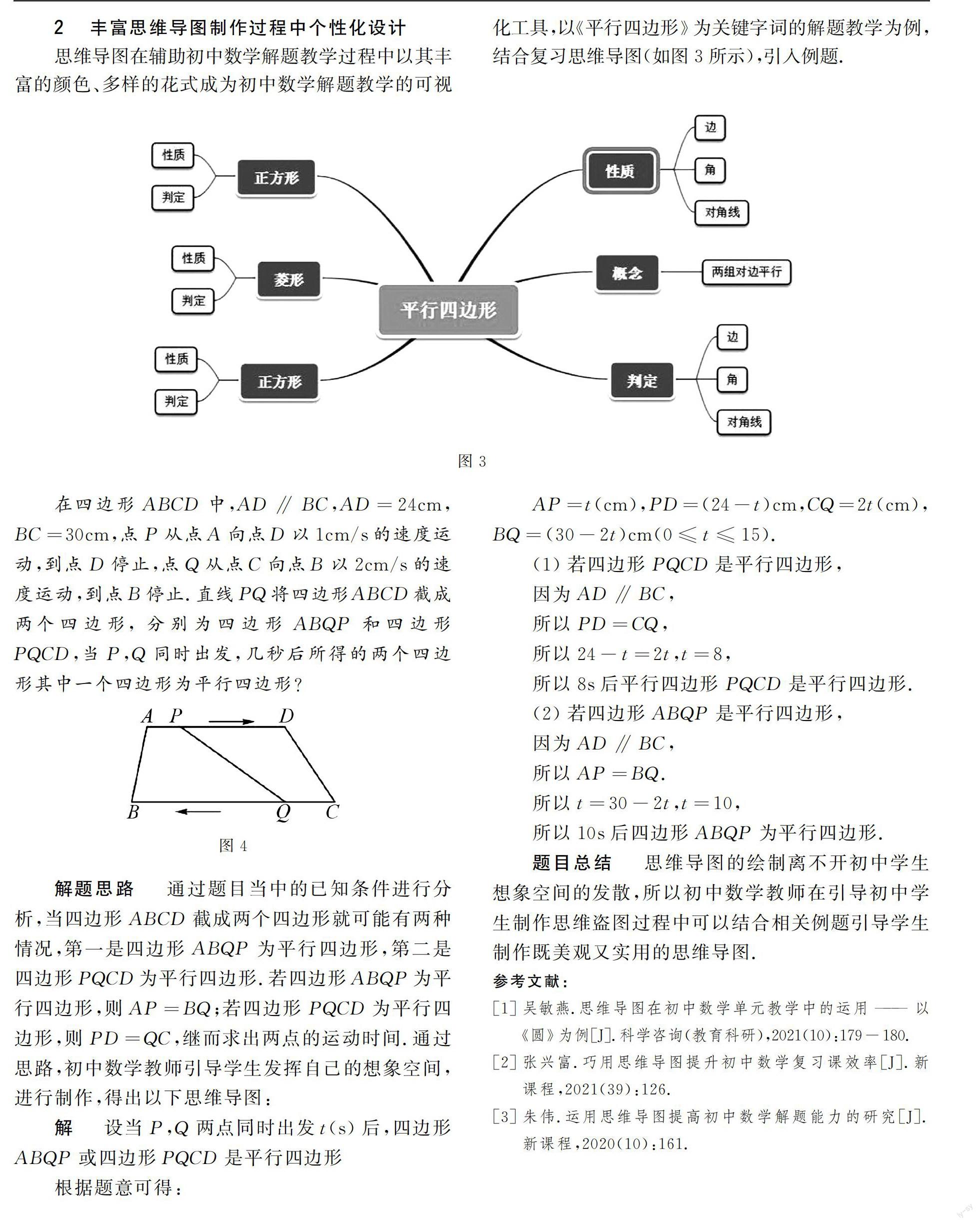
思维导图在辅助初中数学解题教学过程中以其丰富的颜色、多样的花式成为初中数学解题教学的可视化工具，以《平行四边形》为关键字词的解题教学为例，结合复习思维导图（如图3所示），引入例题.

在四边形ABCD中，AD∥BC，AD=24cm，BC=30cm，点P从点A向点D

以1cm/s的速度运动，到点D停止，点Q从点C向点B以2cm/s的速度运动，到点B停止.直线PQ将四边形ABCD截成两个四边形，分别为四边形ABQP和四边形PQCD，当P，Q同时出发，几秒后所得的两个四边形其中一个四边形为平行四边形？

解题思路 通过题目当中的已知条件進行分析，当四边形ABCD截成两个四边形就可能有两种情况，第一是四边形ABQP为平行四边形，第二是四边形PQCD为平行四边形.若四边形ABQP为平行四边形，则AP=BQ;若四边形PQCD为平行四边形，则PD=QC，继而求出两点的运动时间.通过思路，初中数学教师引导学生发挥自己的想象空间，进行制作，得出以下思维导图：

解 设当P，Q两点同时出发t（s）后，四边形ABQP或四边形PQCD是平行四边形

根据题意可得：

AP=t（cm），PD=（24-t）cm，CQ=2t（cm），BQ=（30-2t）cm（0≤t≤15）.

（1）若四边形PQCD是平行四边形，

因为AD∥BC，

所以PD=CQ，

所以24-t=2t，t=8，

所以8s后平行四边形PQCD是平行四边形.

（2）若四边形ABQP是平行四边形，

因为AD∥BC，

所以AP=BQ.

所以t=30-2t，t=10，

所以10s后四边形ABQP为平行四边形.

题目总结 思维导图的绘制离不开初中学生想象空间的发散，所以初中数学教师在引导初中学生制作思维盗图过程中可以结合相关例题引导学生制作既美观又实用的思维导图.

参考文献：

[1]吴敏燕.思维导图在初中数学单元教学中的运用——以《圆》为例[J].科学咨询（教育科研），2021（10）：179-180.

[2]张兴富.巧用思维导图提升初中数学复习课效率[J].新课程，2021（39）：126.

[3]朱伟.运用思维导图提高初中数学解题能力的研究[J].新课程，2020（10）：161.