中职数学课堂教学改革研究

潘旭

摘 要：《中等职业学校数学课程标准》强调通过中等职业学校数学课程的学习，使中职学生获得进一步学习和专业发展所必需的数学知识、数学技能、数学方法、数学思想和活动经验;具备中等职业学校数学学科核心素养，形成在继续学习和未来工作中运用数学知识和经验发现问题的意识、运用数学的思想方法和工具解决问题的能力。而课堂教学关系到教学质量、教学效果，课堂教学改革成为中职学校教学工作的一项重要任务。以数学基础模块下册（第三版）“棱柱”一课为例，探讨中职院校数学课堂教学改革。

关键词：中职数学;课程教学改革;棱柱

党的十九大以来，职业教育改革发展举措不断，《国家职业教育改革实施方案》《职业教育提质培优行动计划（2020—2023年）》《关于推动现代职业教育高质量发展的意见》这三个文件明确了“十四五”期间职业教育改革发展政策框架，职教进入提质培优改革的攻坚关键期。《中等职业学校数学课程標准》强调要培养学生具备一定的科学精神和工匠精神，养成良好的道德品质，增强创新意识，成为德、智、体、美、劳全面发展的高素质劳动者和技术技能人才。

2022年教育部调整中职定位，推动中职学校从原来单纯的“以就业为导向”转变为“就业与升学并重”，抓好符合职业教育特点的升学教育。在保障学生技术技能培养质量的基础上，加强文化基础教育，打开中职学生的成长空间，让中职学生就业有能力、升学有优势、发展有通道。因此，中职院校亟须进行课堂教学改革，培养学生既有专业理论知识又能熟练掌握专业技能，以适应现代社会发展的技术型人才。

现在学生有效注意时间越来越短，想吸引学生投入持续的学习是非常困难的事情。因此，通过有效措施、策略或是手段进行课堂教学改革，在正确的理念下把课程设计成对学生有吸引力并且投入度高的课程，这是很多教师的心愿。下面就以“棱柱”一课为例探讨中职院校数学课堂教学改革。

棱柱是柱、锥、球及其简单组合体这节的起始课，本节课的教学，不仅要帮助学生理解棱柱、棱锥和棱台的概念，把握棱柱、棱锥和棱台的几何特征，认识棱柱、棱锥和棱台这些空间图形，更重要的是引领学生走进几何体，体会研究空间问题的基本思想方法，为学生指明整节学习的路径，充分发挥起始课导学、启思和激趣的功能。

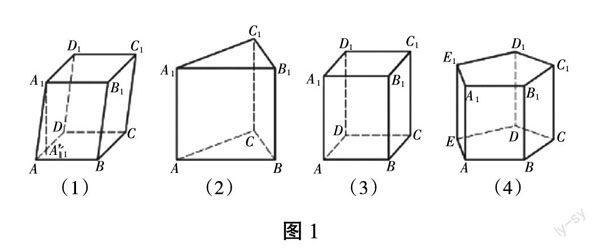
在以往的教学模式中，课堂上先让学生回顾在义务教育阶段学习过的直棱柱，再延伸到像直棱柱那样，由若干个平面多边形围成的封闭的几何体就是多面体，然后再观察如图1所示的多个多面体总结所具有的特征，最后得出棱柱的定义及相关性质，再通过教师教具的展示总结正棱柱的侧面积、全面积及体积公式，并做相关练习题。而在这个教学过程中，学生多为被动地观察、参与到教学任务中来，学习兴趣不高。

因此，教师应建立以学生为主、自学为主、开发为主、动手为主的课堂教学结构，变被动学习为主动学习，以发展智能、突出操作为重点，以启发、点拨、释疑、练习为手段，以开阔思维，发展创造型、技术型、实用型人才为核心，充分利用线下及线上平台，全面提高本节课的教学质量。

一、激活旧知

在班级微信群里发送学习任务单，对以下定义进行填空：多面体、多面体的面、多面体的棱、多面体的顶点、多面体的对角线等。预习棱柱的相关定义，完成表格填写。由于学生基础参差不齐，通过课前任务，可以让基础较弱的学生通过查询网络或是书籍完成填写，在班级群里互相讨论，让所有学生参与到本节知识的学习中来。

二、示证新知

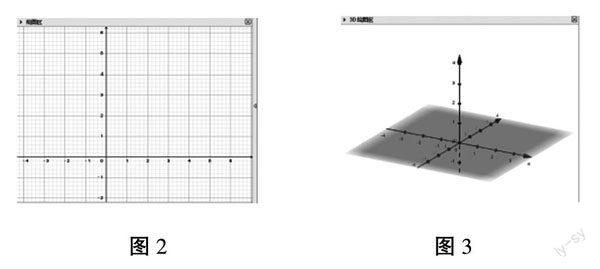
在学习任务单中向学生介绍怎样运用GeoGebra数学软件画出棱柱。以GeoGebra Class 5版本为例，首先在单击界面图2右侧的“”按纽，再点击3D绘图切换界面（如图3），然后进行绘制。学生在课前可以根据自己的实际情况通过手机、电脑、Pad等下载软件，并选择以下图标：先选择画出正多边形，再选择下拉菜单中的，按操作步骤画出自己心目中的棱柱及其展开图。教师发现学生画出各种各样的棱柱，如正三棱柱、正五棱柱、正六棱柱等。在课堂上，教师和学生相互点评图形，使学生加深对棱柱相关定义及性质的理解，并通过3D视图推导正棱柱的侧面积和全面积公式。

在推导侧面积和全面积公式时，学生发现他们用GeoGebra数学软件画出的展开图与教材上不完全一样。以正五棱柱为例，教材上展开图如图4所示，有的学生画出的展开图如图5所示。此时学生就会质疑，这时教师就需要演示这两种展开图，并说明两种图形都是正确的，只是展开的棱不同，所以展开图不同，从而拓宽学生的知识面。一个几何体的展开图不是唯一的，但是正棱柱的侧面积和全面积是相同的，由此推导出公式：S正棱柱侧=ch;S正棱柱全=ch+2S底。

三、应用新知

学生可在应用公式完成教材上的例题及练习题后求解自己画出的正棱柱的侧面积、全面积和体积，并用GeoGebra数学软件下拉菜单中及来验证结果，这极大提高了学生的积极性，完成的学生愿意通过多媒体投屏展示出来，获得学习成就感。

四、融会贯通

将本节课的数学知识应用到实际生活问题中去，教师给出如下题目：我市建了一座商场大楼，底面长85m，宽60m，大楼高28m，它的四周墙壁和顶部准备全部做成玻璃幕墙，一共需要多少玻璃？学生自行求解。

学生很容易由上述公式求出商场大楼的侧面积为S侧=ch=（85+60）×2×28=8120（m2），则商场大楼的顶部面积为S顶=ch=85×60=5100（m2），故商场大楼共需要玻璃为S=S侧+S顶=8120+5100=13220（m2）。

通过本节课的学习，学生不仅总结了棱柱的定义及性质，并从身边出发，收集有关棱柱的图片或是物品，如三棱镜、水立方、茶叶盒等。我国著名数学家华罗庚说过：“就数学本身而言，是壮丽多彩、千姿百态、引人入胜的……认为数学枯燥乏味的人，只是看到了数学的严谨性，而没有体会出数学的内在美。”

在整个教学过程中，学生是学习的主体，互动课堂使学生的学习变被动为主动。学生不仅通过自己的努力获得知识，提高技能，更重要的是能够运用理论指导实践。而教师从单纯的传授知识的教学观念转变为激发学生学习的兴趣与发展学生的智力，在帮助学生掌握基础知识的同时，培养学生的自学能力、独立思考能力、分析问题和解决问题的能力。教师在教好第一课堂的同时，开展丰富多彩的第二课堂活动，处理好课内和课外的关系，两个课堂互相促进，让学生从两个渠道中获取信息，吸收知识，更好地运用多媒体、网络、GeoGebra数学动态软件等先进教学手段，使教学内容更具体、直观，加深学生对知识的理解，加强记忆，使学生发现数学之美，从而提高课堂教学效果。

参考文献：

[1]陈世灵.中职学校课堂教学改革的十大转变[J].广西教育B（中教版），2014（4）：4-5.

[2]李广全，李尚志.数学（基础模块）下册[M].第三版.北京：高等教育出版社，2018.