Matlab工程应用核心内容与讲授方法探讨
潘昀 廖芸蓉 薛大文 白兴兰 李磊

摘要:Matlab作为一门重要的编程语言,目前从工程应用的角度出发,对Matlab重、难点尚未有较系统详细的总结。该文将从三个方面对Matlab核心内容进行讲授:1) 矩阵的处理函数;2) 函数之间的包含关系;3) 图形的编程方法,让初学者加深理解Matlab中的核心内容。
关键词:Matlab;编程;函数;旋转体;图形
中图分类号:G643.2 文献标志码:A
文章编号:1009-3044(2022)31-0046-03
Matlab的全称是Matrix Laboratory,即矩阵和实验室。矩阵在Matlab中应用广泛,尤其在处理数据方面占据优势。目前,高校学生在学习Matlab时,对于很多重点内容细节的学习不够,导致在解决实际工程问题时会遇到麻烦。目前,对于Matlab的研究大多集中在基于Matlab解决实际问题,高云峰[1]利用Matlab对系列力学问题进行了求解;潘昀等[2]以Matlab为载体讲授最小二乘法;许小勇等[3]基于Matlab编写了三次样条插值函数程序;何德峰等[4]基于Matlab软件,对现代控制理论仿真实验教学进行了研究。又或是仅对教学方式进行研究,王海龙等[5]对Matlab在高职数学中的应用进行了研究;韩涛等[7]基于Matlab对电力电子技术实验教学改革进行了研究。
对于Matlab的核心内容的讲授方法介绍相关研究较少,市面上尚有的参考书籍也很少做多简而精。在结合Matlab解决实际问题时,只有对核心内容理解透彻才能够得出准确的结果,因此对Matlab工程应用核心内容的把握以及对核心内容的讲授方法均至关重要。
1 矩阵的处理函数
在Matlab中,矩阵应用中向量和矩阵的创建是基础,而点运算和矩阵的数学运算用于计算实际工程应用中复杂的问题。矩阵在处理数据上,具有高效、灵活、简便、精度高等优点。常见的矩阵中的函数有length、eye、zeros、meshgrid、reshape、diag、repmat等,其中有些函数比较复杂、具有较强的混淆性,不易理解,单看函数介绍,初学者无法完全掌握。对数据进行生成、插值、重新组合等高阶处理时,meshgrid和reshape函数使用较多且具有一定难度。因此,本论文将对meshgrid函数和reshape函数进行详细探讨,通过实例讲授如何高效创建矩阵,让初学者可以对矩阵有一个更加深入的了解。
1.1 meshgrid
1.1.1 meshgrid真实含义
meshgrid函数的本质就是for循环,很大程度提高了Matlab的运算速度,如图1进行了for循环和meshgrid函数创建二维网格和三维数组的对比,可以很直观看出meshgrid函数的优势。在学习meshgrid函数的过程中,存在的难点大致可以分为三点:1) 对meshgrid函数输出和输入的对应关系不清楚;2) 对meshgrid函数生成矩阵的行、列排列规律不理解;3) 三维绘图函数调用meshgrid函数生成的三维数组。本文将详细探讨该函数的基本使用方法并通过一些简单的案例来进行说明。meshgrid函数的调用方法如:[X,Y]=meshgrid(x,y);[X,Y]=meshgrid(x);[X,Y,Z]=meshgrid(x,y,z);[X,Y,Z]=meshgrid(x)。
上述四个语法中x,y,z都是一维数据,在同一语法中矩阵X、Y、Z是同维度矩阵。创建二维网格时,对于X矩阵,向量x确定矩阵中行的值,行数由向量y决定;对于Y矩阵,向量y确定矩阵中列的值,列数由向量x决定。创建三维数组时,数组数量由向量z决定,即向量z中包含元素数量。矩阵X和Y行列生成规律和二维网格一样,矩阵Z中元素值由向量z中元素值决定,每一组对应向量z中的一个元素。使用meshgrid函数相较for循环更为高效、简便,只需要简单一行代码即可代替for循环体,很大程度上提高了运算效率,避免了烦琐的循环。
1.1.2 meshgrid
函数meshgrid一般用于生成二维网格或三维图形所需要的网格数据,进行数据可视化时,可以使用meshgrid函数处理数据进而绘制三维图形。本论文将直接结合实例,让初学者可以更加直观地理解如何使用meshgrid函数数据可视化。
1.2 reshape
在Matlab中,reshape函數又称重构数组。即把矩阵重新进行构造,得到想要的新维度矩阵,但前后两个矩阵中的元素不变,只是排列顺发生了改变。跟meshgrid函数一样,reshape函数的本质也是for循环,其存在也是为了优化for循环,提高Matlab的运算效率。
reshape函数的调用方法有:1) B = reshape(A,sz);2) B = reshape(A,sz1,...,szN)。语法1中,sz是一个大小向量,必须有两个及以上元素构成,决定矩阵B的维度。向量sz的数组元素乘积和矩阵A数组元素的数目相等,也即矩阵B是在以矩阵A的元素数量为限制条件的前提下进行构造的。语法2中,sz1,...,szN,sz1和sz2代表着矩阵的行列数量,在此之后的szN跟矩阵B的维度有关。在使用语法2时,用[]符号代替sz,...,szN中一个维度可以自动计算维度大小。对于矩阵B,是按照矩阵A列从左到右的顺序进行元素读取生成的,元素数量跟矩阵A保持一致。
reshape函数一般用于改变矩阵大小、矩阵维度。可以使二维矩阵和三维矩阵相互转化,当二维矩阵转换成三维矩阵时,可以把数据处理得更加详细直观;当三维矩阵转化为二维矩阵时,可以简化输出结果,使所有维度都排列在一起。无论是二维矩阵转换成三维矩阵还是三维矩阵转换成二维矩阵,其原理都是一样的。
1.3 矩阵创建实例
在解决实际工程问题时,一般需要先对问题进行数学建模,在建模过程中通常涉及矩阵。一般来说,使用矩阵进行绘图可以分为两个阶段,一是绘制网格阶段;二是在网格的基础上绘制旋转体。因此,本节将通过讲授实际应用中使用较多的几个实例来对meshgrid和reshape函数进一步展开说明,让初学者在今后使用Matlab建模时作为参考。
1.3.1 画网格
网格可以分为二维网格和三维网格,使用meshgrid绘制网格是高效、便捷的,为详细展示该函数使用方法,揭开其中原理,教学中应将通过画二维网格、圆弧网格以及波面三个案例进行演示,如图1所示。
1.3.2 画旋转体
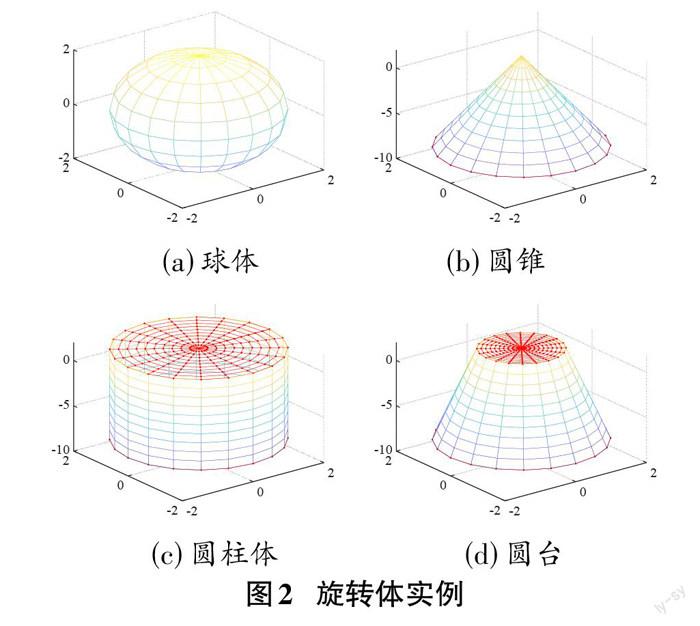
在使用Matlab建模时,模型会涉及各种各样的形状。如对海洋资料浮标建模时,浮标的形状有球型,有圆柱形等。因此,教学中应将以球形、圆柱形、圆锥形、圆台形这几个较为常见的形状作为实例进行讲授,如图2。
2 函数包含关系
当函数过多时,可以选择将不同的函数储存在不同的函数文件中,需要调用时进行读取。一般来说,创建函数有三种方式:1) function命令创建函数文件;2) inline命令创建函数文件;3) 子函数创建函数文件。在编写大规模代码时,会涉及多个函数的创建和调用,因此,必须要先明确函数之间的关系才能保证在使用过程中不会混淆出错。
2.1 函数与函数文件
2.1.1 定义
函数文件是指以function为开头的脚本文件,对function命令结尾加上end语句就构成了一个函数,一个function对应一个end语句。函数内定义的所有变量名对函数而言都是局部的,既不会影响到其他程序文件和函数文件中同样的变量名,也不会被其他影响[11]。函数文件中可以包含一个或多个函数,当包含多个函数时,函数之间的关系就变成了主函数和子函数。
2.1.2 主函数和子函数
在函数文件中,一个M文件只能有一个主函数,且主函数名称和M文件名称必须一致。第一个function创建的函数称为主函数,其他function创建的函数都为子函数,且子函数只能由主函数和主函数文件中其他子函数调用[7]。一个主函数可以有多个子函数,且可以对子函数进行调用,使用子函数可以让代码更加具有观赏性逻辑性。
2.2 函数和程序文件
2.2.1 定义
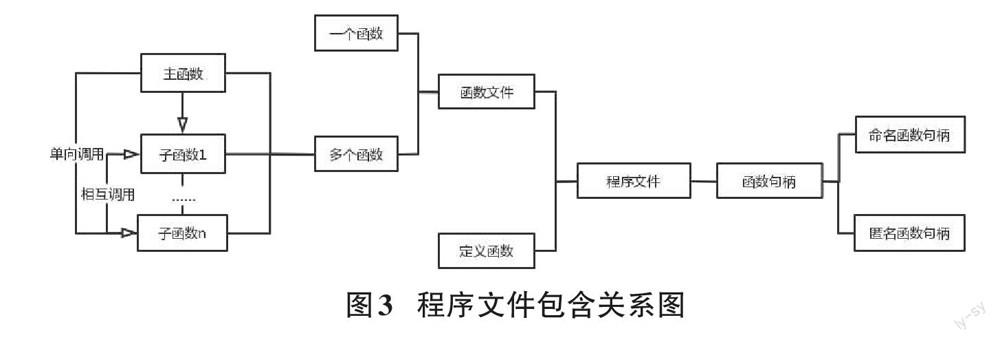
程序文件又称脚本文件,可以将其分为函数文件和定义函数文件两类。由上一节可知,函数文件是以function为开头的程序文件,反之为定义函数文件。定义文件可以对函数文件进行调用,可以用于编写特定的程序并衍生为类,图3为程序文件的包含关系图。
2.2.2 函数句柄
函数句柄是一种引用函数的方法,由“@+函数名”构成。当一个函数的参数是函数时,就需要使用函数句柄,它可以把一个计算方法以变量的形式进行传递。函数句柄可以提高代码的运行速度,创建并运行了函数句柄后,可以随时进行调用。函数句柄的用途可以分为两类,一是用于命名,即创建函数句柄对函数进行调用;二是用于匿名,即传递给函数句柄特定值进行计算后返回。
3 图形编程方法
清晰且直观的图形可以让研究成果显得更加具有逻辑性和可读性。Matlab作为一款集多功能一身的编程软件,在绘图方面极具优势,它可以批量出图,图形的清晰度也令人满意。因此,越来越多的学者都会使用Matlab对数据进行处理出图,熟悉掌握图形的编程方法可以提高处理数据和绘制图形的效率和质量。
3.1 图形输出大小
在绘制二维曲线图时,一般要注意图框的大小尺寸,坐标的设置,字体的大小类型,以及对曲线的标注等问题。[100,100,6.07×100,3.64×100]中前两个数100,100指图框离电脑屏幕左下角的横纵距离,后两个数指输出图形的长宽。其中2.77×100和3.64×100是根据Word页面布局进行换算后得到,使用Word版本为例:A4纸张宽为21cm,其左右边距各位3.18cm,当使用[100,100,100,100]时输出图形,图形的长宽为2.41cm×2.89cm,在这一标准下,Matlab输出图形尺寸和Word之间的关系式为:“100=2.41cm”;故想要输出图形占满Word屏幕,则输出图形长需接近14.64cm,同时为了图形美观,设置输出图形长宽之比为3:5,即输出图形宽需要接近8.78cm。
3.2 动态图方法
除绘制二维曲线图外,通过Matlab绘制的动态图形可以直观生动地反映数据的变化情况,本小节将讲授动态图形的简易画法,为初学者提供思路。for循环中clf和pause命令相结合生成动态图形。
3.3 生成动画
对于三维结构物的运动情况,如海浪的运动,除二维曲线变化图和动态图形外,往往需要动画的形式才能描述清楚其运动情况,在Matlab中,动画是依靠图片形成帧数然后进行播放生成的。主要语句有:O=VideoWriter('文件名.avi'); aviobj.FrameRate=5; close(O)。
4 结束语
本文旨在探讨Matlab工程应用核心内容与讲授方法,通过对矩阵中meshgrid和reshape两个重要函数,函数之间的两个包含关系,以及Matlab中输出图形方法,给初学者提供思路,为今后工程计算和科技论文写作以及编写程序打下基础。
1) 首先介绍了矩阵处理中较为常见且具有一定难度的两个函数meshgrid和reshape,不但对两个函数的使用语法和注意事项进行了讲授,应结合实例对两个函数进行展开介绍说明,让初学者对两个函数有了更加深入的认识。
2) 其次着重讲授了函数之间存在的包含关系,即函数与函数文件和函数和程序文件之间的关系,详细介绍了函数的调用方式、主函数与子函数之间的关系以及函数句柄的使用,让初学者可以更加具体深入了解该如何使用函数。
3) 最后应该学会使用编写绘图模板,包括:二维绘图、動态图形输出、动画输出,在科技论文写作展示成果时,结合图形进行讲授会使得文章更加直观简洁。
参考文献
[1] 高云峰.Matlab求解理论力学问题系列(一)刚体系统及桁架受力问题[J].力学与实践,2021,43(2):256-261.
[2] 许小勇,钟太勇.三次样条插值函数的构造与Matlab实现[J].兵工自动化,2006,25(11):76-78.
[3] 潘昀,刘灿,张建伟,等.浅谈“最小二乘法原理”教学方法[J].科教文汇(中旬刊),2019(9):51-53,56.
[4] 何德峰,俞立,徐建明.基于Matlab的现代控制理论实验教学实践[J].实验技术与管理,2016,33(3):123-126.
[5] 王海龙,徐爱华,贾敬堂,等.浅谈Matlab在高职数学教学中的应用[J].邯郸职业技术学院学报,2021,34(3):37-40.
[6] 韩涛,肖波,詹习生,等.基于Matlab的电力电子技术实验教学改革[J].湖北师范大学学报(自然科学版),2021,41(4):103-107.
[7] Magrab E B.Matlab原理与工程应用with applications from mechanical,aerospace,electrical,and civil engineering[M]. 高会生,李新叶,胡智奇,等译.北京:电子工业出版社,2006.
【通联编辑:闻翔军】
收稿日期:2022-03-16
基金项目:浙江海洋大学研究生一流课程建设项“MATLAB工程计算与优化”(111810641210)
作者简介:潘昀(1989—) ,男,安徽阜阳人,讲师,博士,研究方向为计算工程流体力学。

