对称变换巧转化 破解线段和最值

毛丽丽

考题再现

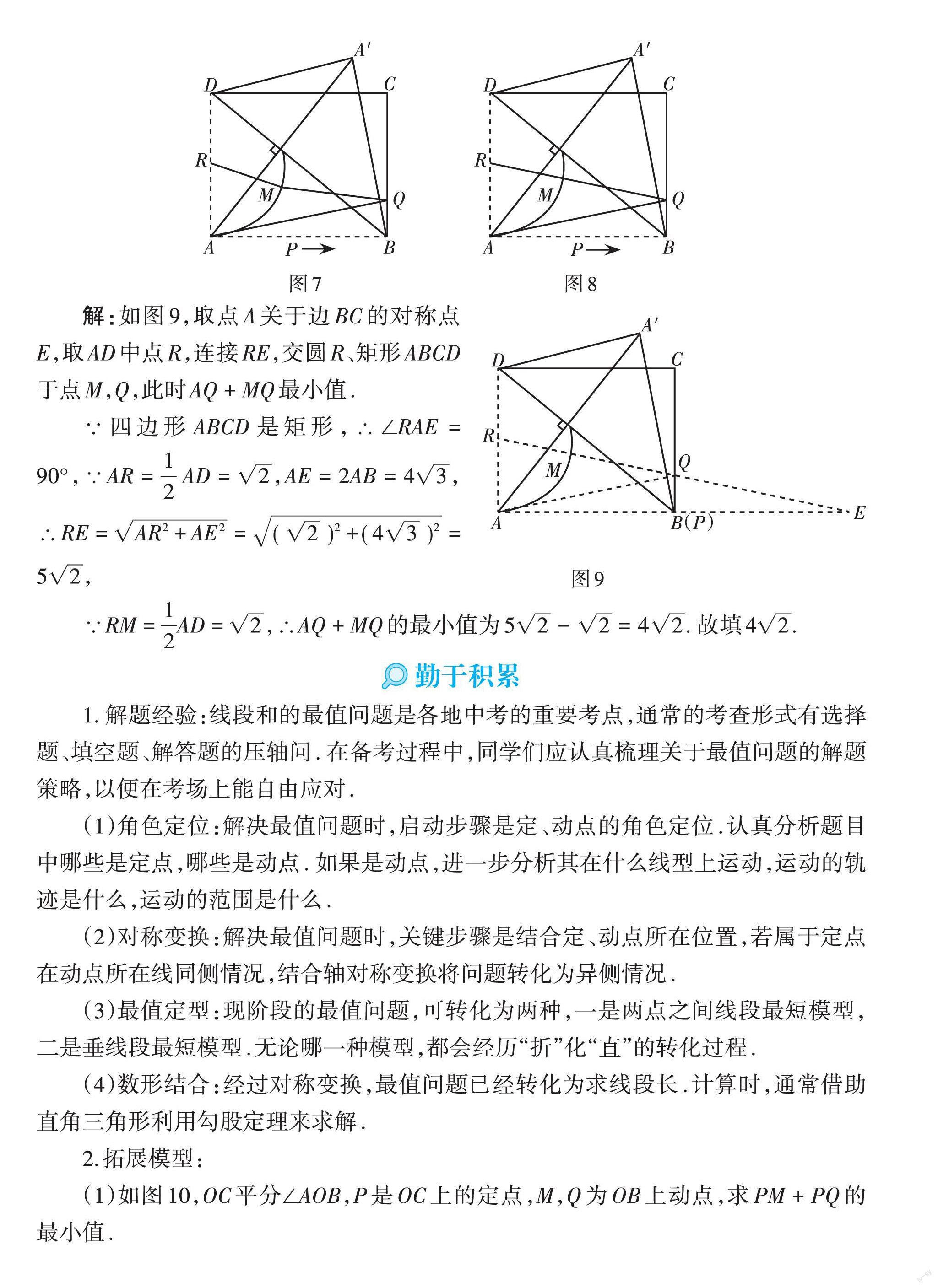
例 （2021·辽宁·盘锦）如图1，四边形ABCD为矩形，AB = [23]，AD = [22]，点P为边AB上一点. 以DP为折痕将△DAP翻折，点A的对应点为点A'. 连接AA'，AA' 交PD于点M，点Q为线段BC上一点，连接AQ，MQ，则AQ + MQ的最小值是.

考点剖析

1.知识点：两点之间线段最短、轴对称图形的性质、90°的圆周角所对的弦是直径、矩形的性质、勾股定理、二次根式计算.

2.数学方法：联想法、对比法、转化法.

3.基本模型：如图2，若∠ACB = 90°，直角顶点C的轨迹为以AB为直径的圆（点A，B除外）;如图3，P为圆O外一点，A为圆O上任一点，当点A运动到点B时，PA取得最小值，当点A运动到点C时，PA取得最大值.

学情分析

（1）相关联想：本题求两线段和的最小值，其中点A为定点，点M，Q为动点，属于“一定两动”的情况，联想相关经验.

关联1：如图4，A，B是直线l的同侧两定点，在直线l上求作一点P，使PA + PB最小.

关联2：如图5，点P是∠MON内一定点，分别在射线OM，ON上求作点A，B，使得PA + PB最小.

关联3：如图6，点P是∠MON内一定点，分别在射线OM，ON上求作点A，B，使PA + AB最小.

（2）对比分析：

关联1：如图4，作点A关于直线l的对称点A'，连接A'B交直线l于点P.此时点P为所求. PA + PB的最小值为线段A'B的长.此种情况属于“两定一动”，与本题不符合，但是也不排除本题可转化为此种情况.

关联2：如图5，过点P作PA⊥OM于点A，PB⊥ON于点B，点A，B为所求. PA + PB的最小值为此时图中A，B所在位置时PA + PB的长.此种情况属于“一定两动”，与本题看似符合.

关联3：如图6，取点P关于射线OM的对称点P'，过点P'作P'B⊥ON于点B，P'B分别交射线OM，ON于点A，B.此时点A，B为所求，PA + AB的最小值为线段P'B的长. 此种情况属于“一定两动”，两动点均在直线上，与本题看似符合.

（3）回归例题：结合上述关联对比分析，深入思考该题本质，其中点A为定点，点Q为线段BC上一点，即属于直线上动点，而动点M的轨迹题目中没有直接给出，因此需要首先明确此问题，然后联想对比已有经验，进而合理转化解决问题.

通过点M的产生来研究点M的轨迹.点M为一对对称点连线与对称轴的交点，所以DP⊥AA'于点M，即随着点P从点A运动到点B的过程中，点M随着点P的运动而运动，但是∠AMD为直角的结论始终保持不变，由此确定动点M的运动路径为弧AM.由于90°的圆周角所对的弦是直径，所以AD为直径，AD 中点为弧AM所在圆的圆心.正因为点M为圆弧上的动点，本题的解决与关联2和关联3的情况不符合，再尝试寻找与关联1的关系，将“一定两动”转化为“两定一动”.

如图7，点M为圆弧上动点，所以RM长度始终保持不变. 关键线段MQ何时有最小值是本题突破口.

如图8，当R，M，Q三点共线时MQ最小.此时两个动线段AQ和MQ联合定长线段RM转化为AQ + RQ，即由两定点A，R来锁定，使得动态问题顺利“着陆”，最终利用“两点之间线段最短”解决问题.

解：如图9，取点A关于边BC的对称点E，取AD中点R，连接RE，交圆R、矩形ABCD于点M，Q，此时AQ + MQ最小值.

∵四边形ABCD是矩形，∴∠RAE = 90°，∵AR = [12AD] = [2]，AE = 2AB = 4[3]，∴RE = [AR2+AE2] = [（2）2+（43）2] = [52]，

∵RM = [12]AD = [2]，∴AQ + MQ的最小值为[52-2=42]. 故填4[2].

勤于积累

1. 解题经验：线段和的最值问题是各地中考的重要考点，通常的考查形式有选择题、填空题、解答题的压轴问. 在备考过程中，同学们应认真梳理关于最值问题的解题策略，以便在考场上能自由应对.

（1）角色定位：解决最值问题时，启动步骤是定、动点的角色定位.认真分析题目中哪些是定点，哪些是动点. 如果是动点，进一步分析其在什么线型上运动，运动的轨迹是什么，运动的范围是什么.

（2）对称变换：解决最值问题时，关键步骤是结合定、动点所在位置，若属于定点在动点所在线同侧情况，结合轴对称变换将问题转化为异侧情况.

（3）最值定型：现阶段的最值问题，可转化为两种，一是两点之间线段最短模型，二是垂线段最短模型.无论哪一种模型，都会经历“折”化“直”的转化过程.

（4）数形结合：经过对称变换，最值问题已经转化为求线段长.计算时，通常借助直角三角形利用勾股定理来求解.

2.拓展模型：

（1）如圖10，OC平分∠AOB，P是OC上的定点，M，Q为OB上动点，求PM + PQ的最小值.

思路分析：如图10，作点Q关于OC的对称点Q'，作MQ[″]⊥OA于点Q[″]，则PM + PQ转化为PM + PQ'，再转化为MQ[″]. 所以PM + PQ的最小值为线段MQ[″]的长.

（2）如图11，点P是∠AOB内一定点，分别在射线OA，OB上求作点M，N，使得△PMN的周长最小.

思路分析：如图11，分别作点P关于OA，OB的对称点P'，P[″]，连接P'P[″]，分别交OA，OB于点M，N，则PM = P'M，PN = P[″]N，△PMN的周长的最小值转化为线段P'P[″]的长.

（3）如图12，[l1][?][l2]，[l1]，[l2]之间距离为[d]，在[l1]，[l2]上分别找M，N两点，使得MN⊥[l1]，且AM + MN + NB最小.

思路分析：求AM + MN + NB的最小值，表面上看是求三条线段和的最小值，但其中MN为定长[d]，所以只需求AM + NB的最小值，而这两条线段没有公共点，没办法直接化“折”为“直”，可借助构造平行四边形AA'NM平移线段来解决（如图12），此时AM = A'N，所以本题转化为求A'N + NB最小.连接A'B即为A'N + NB的最小值，点M，N也随之确定，这样就解决了AM + MN + NB的最小值问题.

（4）如图13，已知△ABC，在边AB，BC，AC上分别求作点P，M，N，使得△PMN的周长最小.

思路分析：求△PMN的周长的最小值，即MP + NP + NM的最小值，三个动点都在直线上，利用轴对称变换化“折”为“直”即可.如图13，作点M关于AB的对称点M'，则MP = M'P;作点M关于AC的对称点M[″]，则NM = NM[″]，所以MP + NP + NM转化成M'P + NP + NM[″].当M'，P，N，M[″]四点共线时，M'P + NP + NM[″]的长最小，为M'M[″]的长.由于∠M'AM[″] = 2∠BAC，为定角，若要M'M[″]最小，则需要AM'最小，即AM最小，当AM⊥BC时即可.