谈谈运用反证法解题的步骤
周文帝

假设原命题不成立,经过正确的推理,最后得出相矛盾的结论,因此说明假设错误,从而证明原命题成立,这样的证明方法叫做反证法.反证法是一种间接证明方法.当遇到一些不容易或者不能从正面进行证明的题目时,可以尝试運用反证法,从问题的反面人手来进行证明.反证法弥补了直接证明方法的不足,在解题中应用广泛,有着不可替代的重要作用.
运用反证法解题的步骤如下:
第三步,得出结论.断定产生矛盾的原因在于开始所作的假设不成立,于是结论q成立,从而间接地证明了命题p?q为真命题.
反证法常适用于证明否定性命题、存在性命题以及含有“至多“至少“唯一”等字眼的命题.
下面举例说明.
例1.已知点A、B、C三点在同一条直线上,求证:过A、B、C三点不能画圆.
证明:假设经过A、B、C三点可以画圆,如图1所示,
设此圆的圆心为O,那么A、B、C三点中的任意两点的连线就是圆O的弦,
根据垂径定理可知,。不仅在AB的中垂线OM上,还在BC的中垂线ON上,
那么过点O有两条直线OM与ON均与AC垂直,显然,这与垂直定理不相符,所以这个假设不成立,则过A、B、C三点不能画圆.
直接证明本题较为困难,不妨从其反面入手,采用反证法进行求证.首先假设过A、B、C三点能画圆,将其作为已知条件,根据垂径定理和三点共线的公理进行推导,得出相矛盾的结论,即可证明结论.
可得a2=2b2,所以a2为偶数,
因此a也一定是偶数,
设存在自然数c,使得a=2c,
则a2=4c2,则2c2=b2,
由于b2是偶数,所以b也是偶数,
可得a,b均为偶数,这与a,b互质相矛盾,
而证明原命题成立.
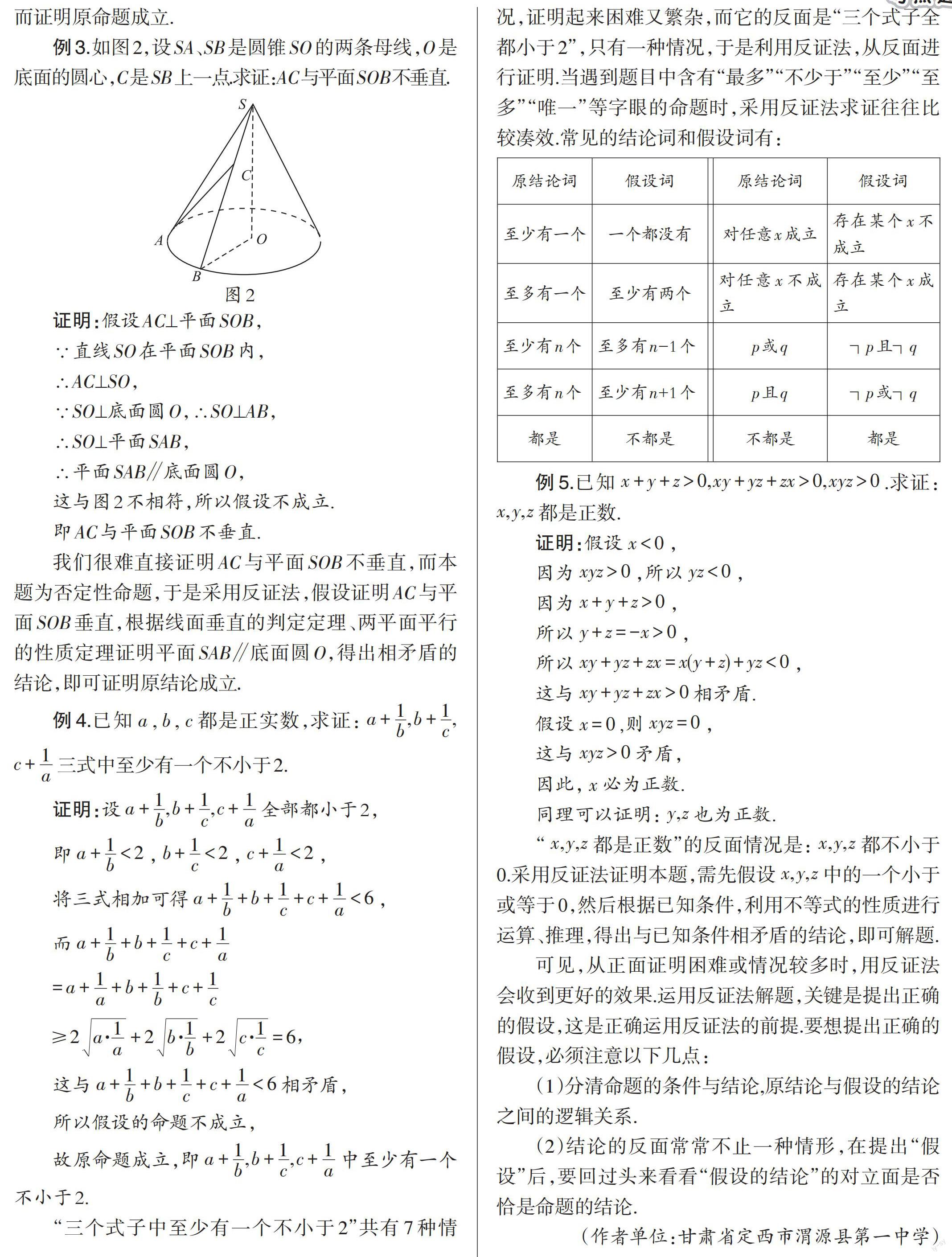
例3.如图2,设S4、SB是圆锥SO的两条母线,O是底面的圆心,C是SB上一点求证:AC与平面SOB不垂直
证明:假设AC⊥平面SOB,
∵直线SO在平面SOB内,
∴AC⊥SO,
∵SO⊥底面圆O,∴SO⊥AB,
∴SO⊥平面SAB,
∴平面SAB∥底面圆O,
这与图2不相符,所以假设不成立.
即AC与平面SOB不垂直.
我们很难直接证明AC与平面SOB不垂直,而本题为否定性命题,于是采用反证法,假设证明AC与平面SOB垂直,根据线面垂直的判定定理、两平面平行的性质定理证明平面SAB∥底面圆O,得出相矛盾的结论,即可证明原结论成立.
所以假设的命题不成立,
“三个式子中至少有一个不小于2”共有7种情况,证明起来困难又繁杂,而它的反面是“三个式子全都小于2”,只有一种情况,于是利用反证法,从反面进行证明.当遇到题目中含有“最多”“不少于”“至少”“至多”“唯一”等字眼的命题时,采用反证法求证往往比较凑效.常见的结论词和假设词有:
例5.已知x+y+z>0,xy+yz+zx>0,xyz>0.求证:
x,y,z都是正数.
证明:假设x<0,
因为xyz>0,所以yz<0,
因为x+y+z>0,
所以y+z=-x>0,
所以xy+yz+zx=x(y+z)+yz<0,
这与xy+yz+zx>0相矛盾.
假设x=0,则xyz=0,
这与xyz>0矛盾,
因此,x必为正数.
同理可以证明:y,z也为正数.
“x,y,z都是正数”的反面情况是:x,y,z都不小于0.采用反证法证明本题,需先假设x,y,z中的一个小于或等于0,然后根据已知条件,利用不等式的性质进行运算、推理,得出与已知条件相矛盾的结论,即可解题.
可见,从正面证明困难或情况较多时,用反证法会收到更好的效果.运用反证法解题,关键是提出正确的假设,这是正确运用反证法的前提.要想提出正确的假设,必须注意以下几点:
(1)分清命题的条件与结论,原结论与假设的结论之间的逻辑关系.
(2)结论的反面常常不止一种情形,在提出“假设”后,要回过头来看看“假设的结论”的对立面是否恰是命题的结论.

