基于优化模型的莱州湾三疣梭子蟹(Portunus trituberculatus)栖息地适宜性研究*
张孝民 王秀霞 李少文 杨艳艳 徐炳庆 李 凡
(山东省海洋资源与环境研究院 山东省海洋生态修复重点实验室 山东烟台 264006)
栖息地适宜性是对栖息地特征与物种在该条件下生存质量的定量描述(易雨君等, 2013), 是当前海洋生态保护领域重要的研究内容之一, 对于生态养护、资源评估、种群动态研究都具有重要的理论和现实意义(邹易阳等, 2016)。在人类活动不断加剧和气候变化的大背景下, 全球生物多样性正处于持续的快速丧失中(徐炜等, 2016), 其中栖息地的减少已经成为物种和局部种群绝灭的重要原因(邓文洪, 2009; Keinathet al, 2017)。三疣梭子蟹(Portunus trituberculatus)生命周期短、繁殖力强、经济价值高(林群等, 2015), 捕捞数量占全世界经济蟹类的四分之一左右(Liuet al, 2013)。莱州湾位于渤海南部, 是赫赫有名的“莱州梭子蟹”的产地, 更有黄河和小清河等众多河流入海, 湾内基础饵料丰富, 水温盐度适宜, 是包括蟹类在内的众多经济性海洋生物的产卵和栖息场所。近几十年来, 受环境污染、过度捕捞等人类活动的影响, 莱州湾海洋生境遭到破坏, 众多生物的栖息地出现破碎化现象, 部分海区呈现荒漠化趋势。与其他海洋生物一样, 三疣梭子蟹的栖息地也在不断减少, 资源量持续衰退(卢晓等, 2018)。栖息地适宜性评价在内陆河流及湖泊生物资源中运用较为广泛, 在海洋中的运用起步较晚(龚彩霞等, 2011), 近年来研究集中在大洋鱼类生物资源, 对于近海生物资源有较大的应用空间, 国内有关三疣梭子蟹栖息地适宜性的研究尚未见报道, 亟待开展相关研究。
HSI 模型是进行栖息地适宜性定量评价的经典方法, 该方法最早由美国地理调查局国家湿地研究中心鱼类与野生生物署于20 世纪80 年代初提出(U.S.Fish and Wildlife Service, 1981)。GAM 模型常用来分析生物丰度和环境变量的非线性关系(Woodet al,2002), 可以在HSI 模型中选择环境变量。BRT 模型基于决策树理论的学习方法, 可有效计算出变量因子对模型建立的贡献大小(De’ath, 2007), 生成多重回归树, 获取变量的权重分布。
本文构建了四种HSI 模型, 包括普通HSI 模型;GAM 优化HSI 模型; BRT 优化HSI 模型; GAM 和BRT优化HSI 模型, 对莱州湾三疣梭子蟹栖息地适宜性进行研究, 以期摸清资源分布状况, 明确适宜的环境特征, 全面了解其栖息地生存质量, 为三疣梭子蟹栖息地保护和莱州湾生态修复提供帮助。
1 材料与方法
1.1 数据来源和预处理
三疣梭子蟹数据来源于2010~2020 年夏季底拖网调查, 调查区域为莱州湾海域(119°00′~120°15′E,37°12′~37°40′N), 调查站位每年20 个(图1)。调查船只功率260 kW, 调查网具为单船底拖网, 网口周长30.6 m, 囊网网目20 mm, 拖曳时网口宽度约8 m。
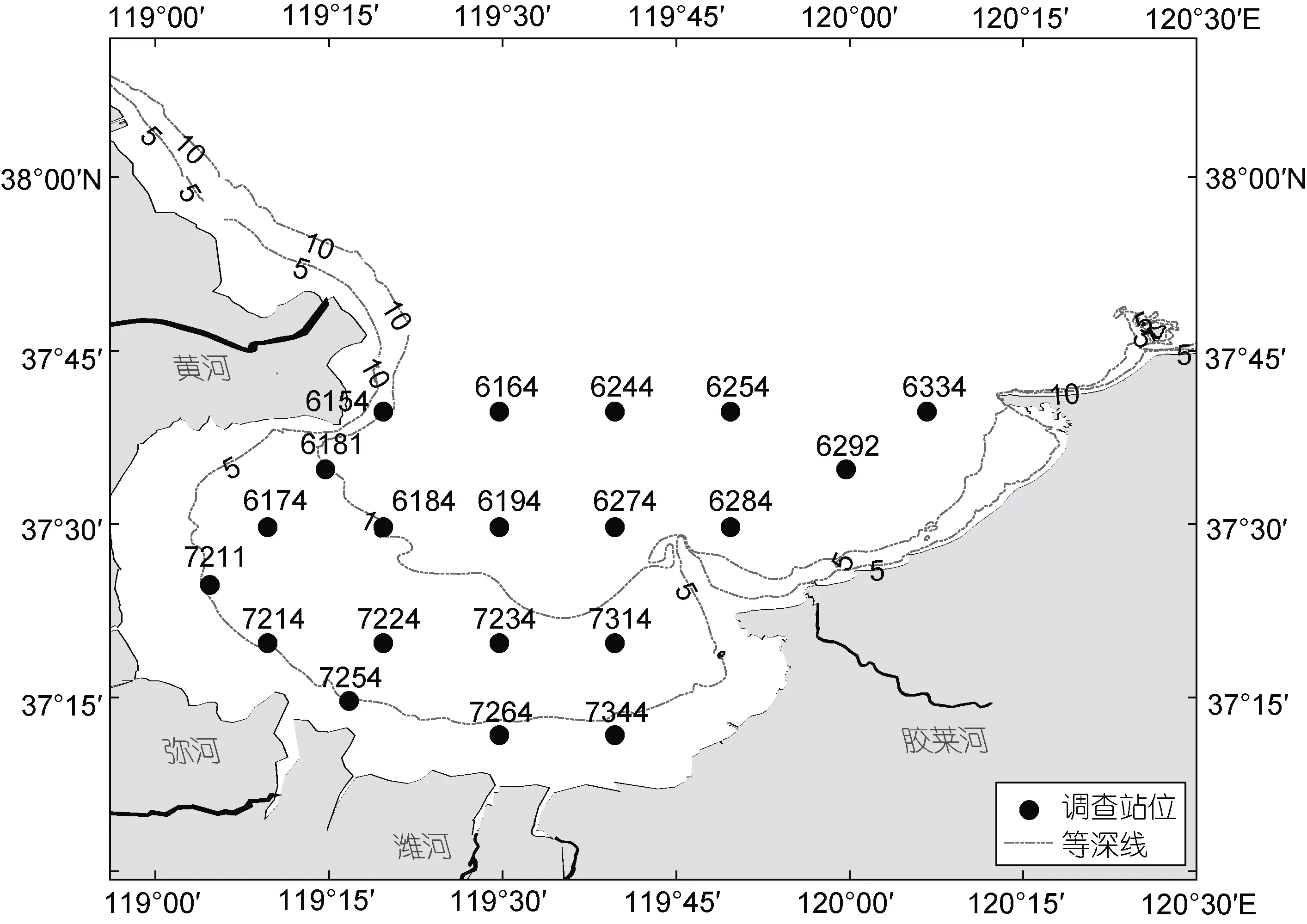
图1 莱州湾三疣梭子蟹调查站位Fig.1 Sampling stations of P. trituberculatus in the Laizhou Bay
环境数据利用美国 ORI-ON520M-01A 便携式YSI 水质分析仪现场测定, 内容为水深(depth,D)、底层水温(bottom sea temperature, BST)、底层叶绿素(bottom sea chlorophyll, BSC)、底层盐度(bottom sea salinity, BSS)。大型底栖生物(Macrozoobenthos, Mzb)取样使用开口面积为0.05 m2箱式采泥器采集, 每个站位取2 个平行样, 使用0.05 mm 的网筛分选大型底栖动物, 样品的保存、处理、计数和称量等均按《海洋调查规范》GB/T 12763.6—2007 (中华人民共和国国家质量监督检验检疫总局等, 2008)进行。
以调查网具拖速3 kn、拖网时间1 h 为基准, 根据各站位实际拖网时间对调查数据进行标准化处理,将其换算为单位时间的生物量(biomass, Bio) (g/h)和个数(individual, Ind) (ind./h), 以表征三疣梭子蟹的资源丰度。
1.2 研究方法
1.2.1 变量因子的选择 GAM 是一种非参数化的多元线性回归模型, 可以用来表示响应变量和解释变量的非线性关系, 本文利用GAM 模型选择HSI 模型中的变量。GAM 模型通常表示为:
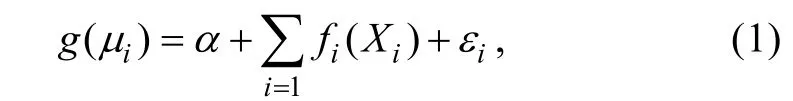
式中,g为链接函数,μi=E(Yi),Xi为第i个响应变量的解释变量,β为模型估计参数,Yi为第i个响应变量,fi为平滑函数。将变量因子逐渐加入GAM 模型中, 选取AIC 值最小的模型作为最佳模型(Damalaset al,2007)。AIC 值的计算(Reid, 2003)如下:

式中,m为模型中参数的个数,n为观察值(数据样本)的个数, RSS 为残差平方和。
1.2.2 变量因子权重分析 BRT 模型基于变量因子的相对贡献确定其在HSI 模型中的权重(Changet al, 2010; Yiet al, 2016), BRT 方法是在运算过程中随机抽取一定量的数据, 分析自变量对因变量的影响程度, 而剩余数据用来对拟合结果进行检验, 对生成的多重回归树取平均值输出, 从而得出自变量对因变量的相对重要性(Keinathet al, 2017)。本文使用R 4.0.3 中“GBM”包的“GBM.STEP”功能实现BRT 模型,其中抽样率(Train. Fraction)设置为 0.8, 重复循环计算1 000 次, 获取每个环境变量的相对贡献, 即环境变量的权重分布。
1.2.3 HSI 模型 首先, 利用样条平滑函数建立变量因子与适宜性指数(suitability index, SI)的关系模型,分别以生物量Bio 和个数Ind 建立SI, 调查数据中Bio和Ind 最小值为0, 三疣梭子蟹在调查海域资源密度不均, 最大值和最小值量级差距较大, 直接以Bio 和Ind 数据建模会降低SI 指数精度, 本文对环境变量进行分组, 以各组距范围内Bio 和Ind 的总和建立每个组距下的SI。SI 的取值范围为0~1, 一般认为0.7~1之间是适宜的栖息环境范围(Brooks, 1997; Xueet al,2017), 计算公式如下:
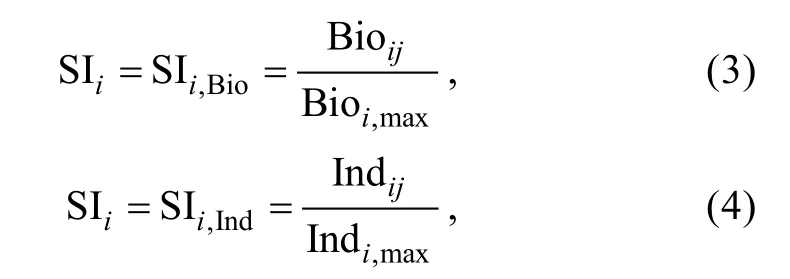
式中, SIi为i环境变量的适宜性指数, SIi,Bio为以生物量Bio 为基础建立的适宜性指数, SIi,Ind为以个数Ind为基础建立的适宜性指数, Bioij为i环境变量的j组距的Bio, Bioi,max为i环境变量的最大Bio, Indij为i环境变量的j组距的Ind, Indi,max为i环境变量的最大Ind。
HSI 模型是由SI 模型构建的综合模型, 取值范围为0~1, 代表栖息地适宜性“差”到“好”, 本文采用算数平均法(arithmetic mean model, AMM)和几何平均法(geometric mean model, GMM)来构建HSI 模型, 计算公式分别为:
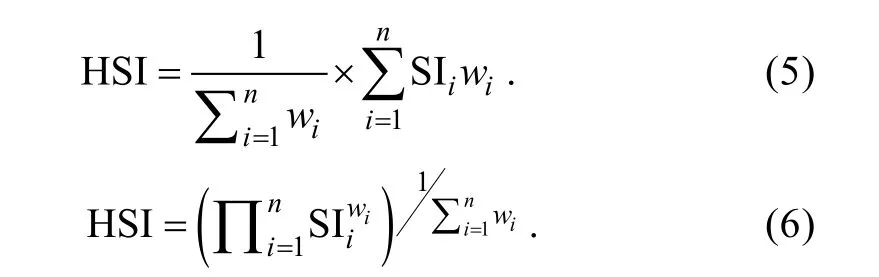
1.2.4 HSI 模型的比较和验证 采用2010~2018 年数据构建HSI 模型, 包括四种类型, 分别为: 普通HSI 模型; GAM 优化HSI 模型(GAM 对变量进行筛选后建立的HSI 模型); BRT 优化HSI 模型(BRT 对变量权重进行优化建立的HSI模型); GAM和BRT优化HSI模型。通过Pearson 检验2020 年实测值HSI 和模型预测值HSI 的相关性, 采用ArcGIS 10.2 普通Kriging 插值法绘制2020 年莱州湾三疣梭子蟹HSI 地图。
2 结果
2.1 变量因子的选择和权重分析
以生物量表征资源丰度的GAM 模型(表1), 依次选取了D、BST、Mzb 密度和BSS 组成AIC 值最小的模型, 累计解释方差为49.3%,D和BST 与生物量极显著相关(P<0.01), Mzb 密度和BSS 与生物量显著相关(P<0.05)。以尾数表征资源丰度的GAM 模型, 依次选取了D、BST、BSS 和Mzb 密度组成AIC 值最小的模型, 累计解释方差为43.5%,D、BST 和BSS与生物量极显著相关(P<0.01), Mzb 密度与生物量显著相关(P<0.05)。

表1 以生物量和尾数表征资源密度构建的GAM 模型Tab.1 P. trituberculatus abundance shown in the GAM model constructed by using biomass and mantissa
由图2 可知, 以生物量和尾数表征资源密度构建的BRT 模型变量因子的相对贡献顺序相同, BSS 的相对贡献最大, 分别为26.9% (生物量)和23.5% (尾数),BSC 的相对贡献最小, 分别为 12.2% (生物量)和11.4% (尾数), 其他因子的相对贡献大小依次为BST、D和Mzb 密度, 区间范围为19.0%~23.3%。
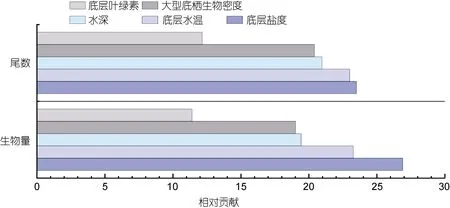
图2 以生物量和尾数表征资源密度构建的提升回归树模型Fig.2 P. trituberculatus abundance shown in the BRT model constructed in biomass and mantissa
2.2 变量因子与生物量和尾数的适宜性指数关系模型
从变量因子的适宜性指数曲线(图3)可以看出,以生物量和尾数表征资源丰度拟合的三疣梭子蟹适宜栖息环境范围(SI>0.7)基本相同。BST 的适宜范围为27.2~28.5 °C, BSS 的适宜范围为25.5~30.5,D的 适宜范围为 9.0~10.5 m, Mzb 密度的适宜范围为2 900~3 100 个/m2, BSC 浓度的适宜范围为 13.5~14.5 mg/m3。
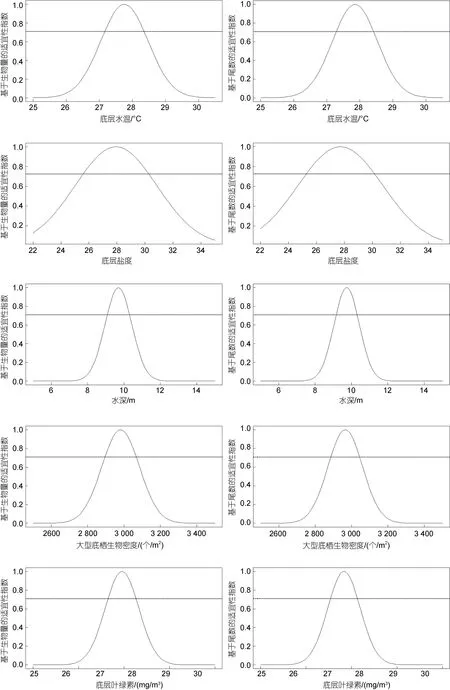
图3 以生物量和尾数表征资源丰度与环境因子的适宜性指数曲线Fig.3 Fitted suitability index (SI) curves based on the relationship between P. trituberculatus abundance in terms of biomass and mantissa and environmental factors
2.3 HSI 模型的比较和验证
以生物量表征资源丰度的GAM 和BRT 优化算术平均模型, 与 2019~2020 实际调查的生物量数据Pearson 相关系数最高, 为0.653, 表明预测值与实测值有较强的相关性, 最优模型具有较强的预测能力。总体看来, 优化后的HSI 模型均好于普通HSI 模型,BRT 优化的模型略好于GAM 优化的模型, GAM 和BRT 优化的模型好于其他3 种模型(表2)。此外, 生物量表征资源丰度的模型好于尾数表征资源丰度的模型,算术平均模型的相关系数高于几何平均模型。
2.4 莱州湾三疣梭子蟹栖息地空间分布
根据GAM 和BRT 优化的算术平均HSI 模型预测结果可以看出, 伏季休渔结束前三疣梭子蟹主要分布在莱州湾南部、东南部和东北部海域, 中部和西南部海域分布较少, HSI 值较低(图4)。模型预测结果与2020 年实际调查的三疣梭子蟹分布情况大体相符,以生物量表征资源丰度的HSI 模型预测的三疣梭子蟹最适海域(HSI>0.7)范围明显大于以尾数表征资源丰度的HSI 模型, 以生物量表征资源丰度的HSI 模型对资源丰度较高区域的预测更加准确。
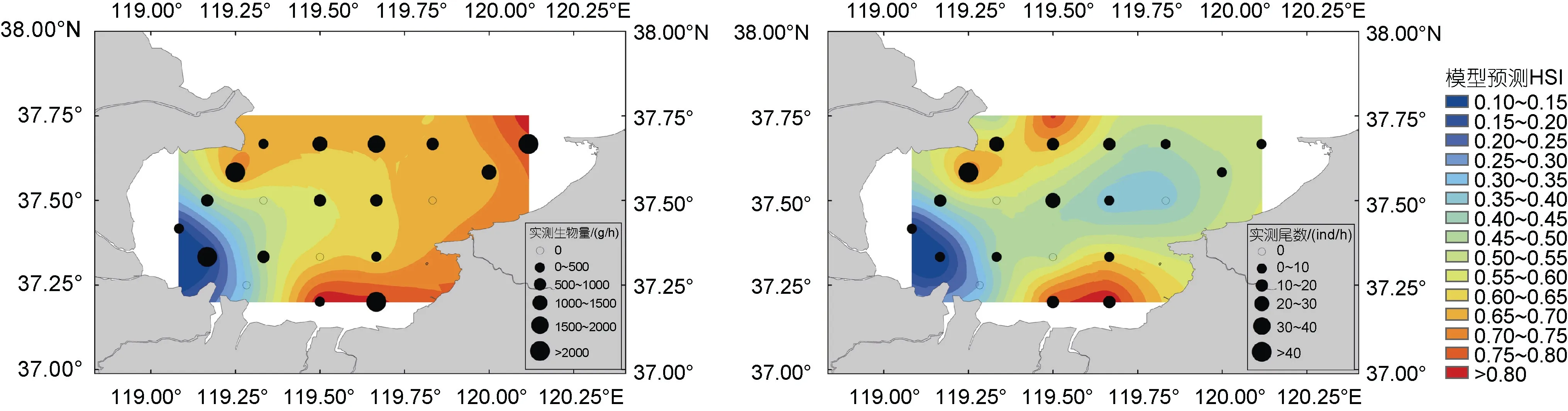
图4 2020 年莱州湾三疣梭子蟹栖息地优化模型预测结果与实际调查情况分布图Fig.4 Spatial distribution of observed abundance of P. trituberculatus in 2020 overlaid with the predicted HSI values based on optimized HSI models
3 讨论
3.1 HSI 模型的优化
生物的栖息地受多种因子的影响, 不同因子的影响大小不同, 合理选择影响因子和设置各因子的权重是优化HSI 模型的两种主要方法。本研究分别采用GAM 模型对三疣梭子蟹影响因子进行选择和BRT模型设置因子权重, 结果(表2)显示BRT 优化模型好于GAM 优化模型, 说明在对HSI 模型优化的过程中,权重设置比因子选择更加重要, 与Zhang 等(2020)研究结果一致。通过查阅文献资料基本可以囊括研究对象栖息地的大部分影响因子, 加上专家知识的判断筛选重要因子, 可以比较准确的完成因子选择的过程(龚彩霞等, 2011), 但权重设置受不同研究海域和不同研究对象的影响较大, 专家无法获得足够的信息对不同因子权重准确设置(Tianet al, 2009), 本研究利用BRT 模型设置因子权重, 与非优化模型相比更具科学性和针对性, 将因子影响程度大小定量表示, 这也是导致权重设置比因子选择优化效果更好的原因。但仍不能忽视GAM 模型对因子选择的重要性, 综合利用GAM 模型和BRT 模型才能构建最佳的HSI 模型。
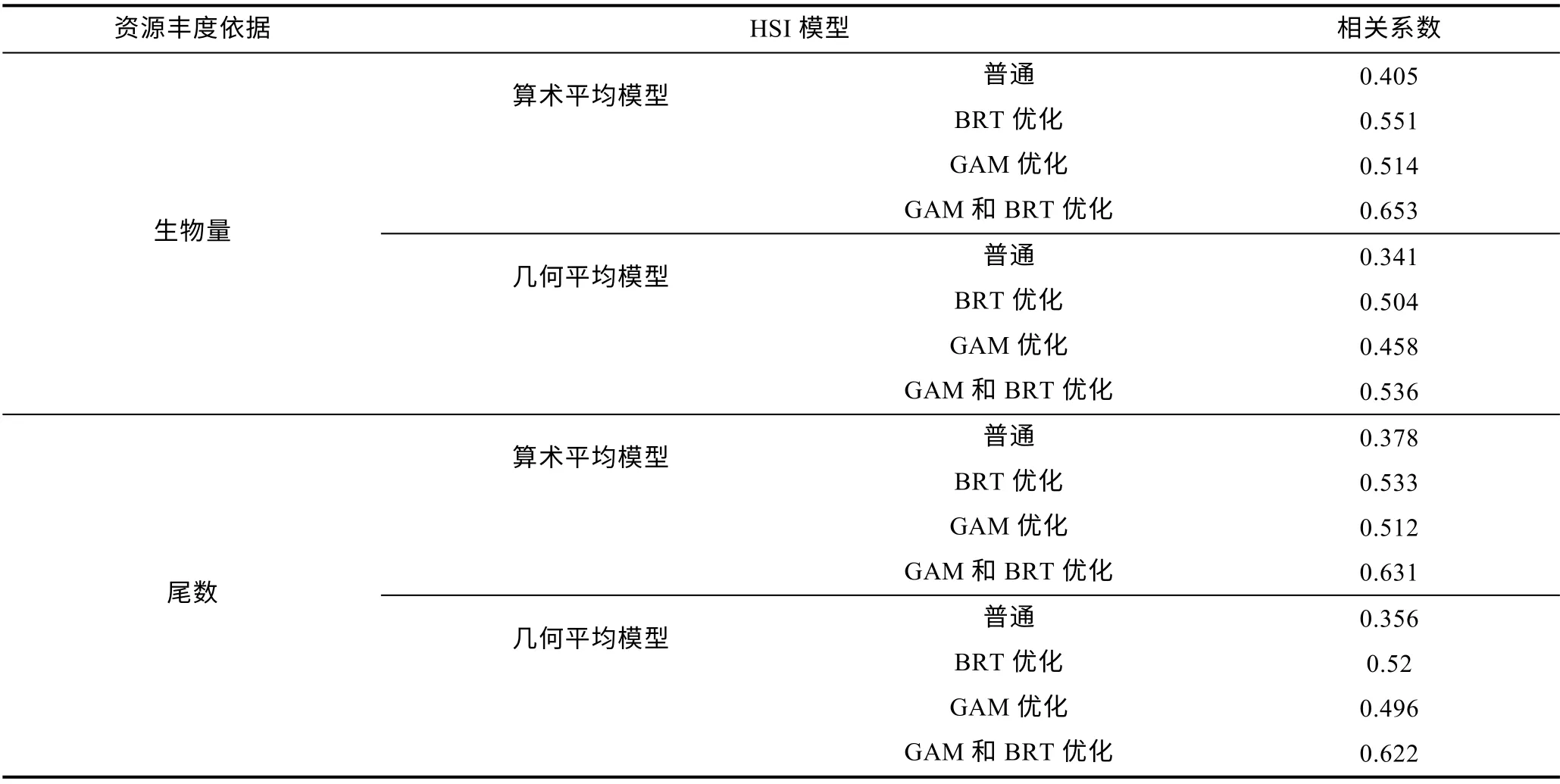
表2 不同HSI 模型预测值与2019~2020 年实际调查数据的Pearson 相关检验结果Tab.2 Results of the Pearson correlation in different HSI model-predicted values and the actual survey data in 2019~2020
研究对象资源丰度指标的选取也是影响HSI 模型建模效果的重要因素, 主要的资源丰度指标包括渔获量(范秀梅等, 2020)、渔获尾数、作业次数、单位捕捞努力量渔获量(catch per unit effort, CPUE) (刘瑜等, 2021)、生物量和渔获密度(朱承之等, 2020)等,相关研究大都采用单一指标描述资源丰度, 本文比较了生物量和尾数表征三疣梭子蟹资源丰度对构建HSI 模型的影响, 发现以生物量表征资源丰度的模型好于尾数, 在GAM 模型的累计解释率也相对较高,可能的原因是三疣梭子蟹个体大小差距较大, 部分站位大型个体较多, 用尾数表征降低了该区域的资源丰度, 但在适宜性指数曲线拟合得到的适宜栖息环境范围基本相同。范秀梅等(2020)分别基于渔获量和作业次数表征日本鲭鱼的资源丰度建立HSI 模型,发现两种方法在预报渔场上精度相差不大, 原因是日本鲭渔船作业次数和渔获量通常成正比关系, 作业次数反映了渔船的集中程度和渔民对产量的满意度(Bordalo-Machado, 2006), 作业次数多表明该海域有很高的渔获量。Tian 等(2009)比较了基于CPUE 和作业次数建立的西北太平洋柔鱼HSI 模型, 结果表明,基于CPUE 的HSI 模型高估了柔鱼的最佳栖息地范围,基于作业次数的HSI 模型能更好地定义柔鱼的栖息地范围。因此, 在选取资源丰度指标时, 应充分考虑研究对象的生物学以及作业方式等特性, 并采用多种指标表征资源丰度, 以获得更好的HSI 模型。此外,HSI 模型的计算方法中, 算术平均法AMM 普遍具有较高的效果(陈新军等, 2009), 本文研究结果也证明了AMM 的优势, 但相关研究表明GMM 对SI 的极大值和极小值较敏感(Vinagreet al, 2006)。
3.2 三疣梭子蟹栖息地的影响因素
莱州湾三疣梭子蟹冬季在渤海10~30 m 水深较深海域越冬, 4 月开始生殖洄游, 到3~5 m 深的港湾或河口等浅海附近海域产卵, 8 月大多数三疣梭子蟹度过产卵期, 进入索饵育肥期, 是三疣梭子蟹资源量最高的时期, 9 月伏季休渔结束后, 高强度的捕捞会使资源量迅速下降, 人为因素成为主导三疣梭子蟹栖息地分布的决定因素, 环境因素影响力下降(Tianet al, 2009), 因此8 月伏季休渔结束前是研究三疣梭子蟹栖息地适宜性的最佳时期。本文研究了影响莱州湾三疣梭子蟹的部分环境因子和生物因子, GAM 模型和BRT 模型结果均表明BST、BSS 和D对其栖息地影响较大, 与吴强等(2016a)研究结果相似。三疣梭子蟹是广盐性蟹类, 但其 BSS 的最适范围为25.5~30.5 (图3), 夏季雨水丰富, 莱州湾淡水入海量增加, 近海盐度变化成为影响三疣梭子蟹栖息地的最主要因素(图2)。三疣梭子蟹最适栖息地的BST 范围为27.2~28.5 °C, 水温不仅是决定三疣梭子蟹的季节性洄游的主要因素, 夏季是索饵育肥的重要时期,水温过高会降低其体内消化酶的活性, 影响摄食行为(廖永岩等, 2008), 进而对栖息地分布产生影响。莱州湾大部分区域水深小于10 m, 最大水深18 m, 水深较浅的近岸水域是三疣梭子蟹产卵栖息的重要场所, 水深的变化会引起水温、盐度和营养盐等的改变,对栖息地分布产生影响, 本文研究发现伏季休渔结束前三疣梭子蟹在莱州湾的最适水深为9.0~10.5 m。相关研究表明三疣梭子蟹分布与底栖生物的关系密切(吴强等, 2016b), 本文研究认为 Mzb 密度为 2 900~3 100 个/m2时是三疣梭子蟹最适范围, 底栖生物是大型甲壳类的重要食物来源, 三疣梭子蟹与日本蟳、口虾蛄和中国明对虾之间存在较强的食物竞争关系(李凡等, 2021), 导致底栖生物密度成为限制其栖息地分布的影响因素, 夏季莱州湾饵料食物较为丰富, 底栖生物与水温和盐度的影响相比较小, 在食物缺乏季节或海域, 底栖生物的影响力将增强。
3.3 夏季莱州湾三疣梭子蟹栖息地空间分布
结合实际调查数据以及HSI 模型的预测结果, 夏季莱州湾整体表现为近岸海域比离岸海域更适合三疣梭子蟹栖息, 这与徐炳庆等(2021)的研究结果一致,8~9 月份伏季休渔结束前水温较高, 三疣梭子蟹尚未进入越冬洄游阶段, 集中分布于近岸海域。本研究调查船只为底拖网渔船, 无法在水深低于5 m 海区设置站位, 如采用小型船只或其他作业方式对浅海三疣梭子蟹资源进行调查, 将使近岸资源好于离岸资源的趋势更加明显。2020 年莱州湾西南部近岸海域在HSI 模型预测中栖息地适宜性较差, 主要原因为7211站位和7214 站位底层平均水温30 °C, 底层平均盐度23.8, 均处于适宜性指数曲线SI 较低的位置, 导致HSI 值较小, 成为不适宜三疣梭子蟹栖息的海域。但在2020 年的实际调查中, 7214 站位生物量较高, 为2 196 g/h, 可能的原因是站位设置中环境数据是与三疣梭子蟹资源数据同步, 近岸海域温盐环境变化较大, 站位设置稀疏使得环境数据的获取出现偶然性,在以后的调查研究中, 应当对近岸海域环境监测站位设置更加紧密, 以获取更加准确地数据, 提高栖息地预测的精确性。
4 结论
本研究运用GAM 模型和BRT 模型在建模过程中对HSI 模型进行了优化, 优化模型对适宜栖息地预测效果均好于未优化模型, 优化模型对莱州湾三疣梭子蟹栖息地适宜性有较强的预测能力。优化模型显示BST、BSS 和D对三疣梭子蟹栖息地影响较大, 莱州湾南部、东南部和东北部是夏季三疣梭子蟹的适宜栖息海域。

