一类食饵-捕食模型的稳定性和Hopf分支的存在性
姚佳佳, 沈 维
(兰州交通大学 数理学院, 兰州 730070)
0 引 言
食饵-捕食模型对保持自然界中生物种群之间的关系有重要作用. 为更好地反映不同种群的特定特征, 目前对具有不同功能食饵-捕食模型的研究已得到广泛关注[1-6]. Aziz-Alaoui等[7]提出了修正的Leslie-Gower模型:

(1)
其中u和v表示相对于时间t的种群密度,r1,b1,a1,k1,r2,a2,k2为模型中正的参数.文献[1]证明了模型(1)的有界性和正不变吸引集的存在性, 得到了该模型正平衡点全局稳定性的条件.Zhu等[8]研究了修正的Leslie-Gower捕食-食饵模型:
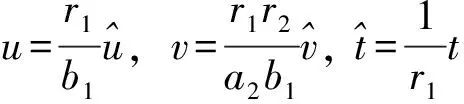

(2)

但在自然界猎物捕食食饵转化为自身能量的过程中, 存在一定的时间间隔, 从而使结果产生差异, 因此本文考虑加入时滞τ代替时间间隔.基于模型(2), 本文考虑时滞捕食模型:

(3)

1 常微分方程正平衡点的稳定性
下面利用文献[12]的方法讨论系统(3)正平衡点U0的稳定性和Hopf分支.在正平衡点U0处线性化系统(3), 得

(4)
系统(3)的特征方程为

(5)
当τ=0时, 方程(5)变为

(6)

定理1当τ=0时, 系统(3)的正平衡点U0是局部渐近稳定的.


(7)
对于系统(3)的任意解u(t),v(t), 有

(8)
证明: 由于当t>0时,u(t)和v(t)非负, 因此

(9)

(10)


(11)

由引理1进一步可得如下结论:


(12)
对于系统(3)的任意解u(t),v(t), 有

(13)


(14)
证明: 由式(7)~式(14)可得
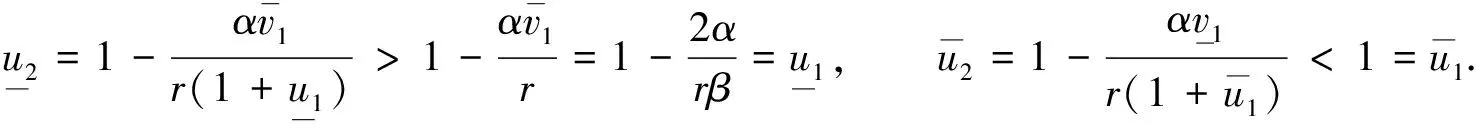
(15)


(16)
则当n≤k时, 由方程(12)有
同理可得
证毕.

(17)
从而由方程(17)可得如下结论:

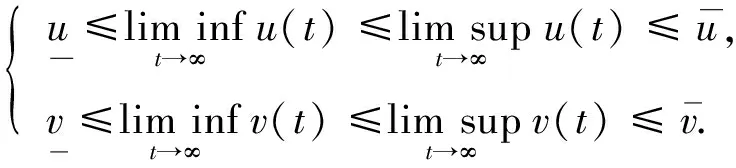
(18)
定理2假设rβ>2α成立, 则系统(3)的唯一正平衡点U0是全局渐近稳定的.
证明: 假设引理1的条件成立, 则由式(17)可得

(19)


(20)
而当rβ>2α成立时, 有

(21)
2 时滞微分方程正平衡点的稳定性
下面考虑时滞τ对系统(3)正平衡点U0稳定性的影响.在方程(5)中令
假设方程(5)有一对纯虚根λ=±iω(ω>0), 则
-ω2+ia1ω+(b1iω+b0)(cos(ωτ)-isin(ωτ))=0.
分离实、 虚部可得

(22)
将式(22)等号两边平方相加, 得

(23)

h(z)=z2+pz+q=0.
(24)


(25)
由方程(25)可知, 相应于ω的τ满足

(26)

证明: 将λ(τ)代入式(5)并关于τ微分, 可得

(27)
注意到
[λ(b1λ+b0)]τ=τj=-b1ω2+ib0ω,
(28)
[(2λ+a1)eλτ]τ=τj=[-2ωsin(ωτj)+a1]+i[-2ω+a1sin(ωτj)].
(29)
由式(27)~(29), 易得

由引理5进一步可得如下结论:
定理3假设ω由式(25)给出,τj(j=0,1,2,…)由式(26)定义, 则:
1) 当τ∈[0,τ0)时, 系统(3)的正平衡点U0是局部渐近稳定的;
2) 当τ>τ0时, 系统(3)的正平衡点U0是不稳定的;
3) 当τ=τj(j=0,1,2,…)时, 系统(3)在U0处出现Hopf分支.
3 数值模拟
下面利用MATLAB软件包和求解常微分方程初值问题的数值方法对本文所得理论结果进行数值验证, 结果分别如图1~图3所示.

图1 当α=1, β=2, r=2, s=2时, 系统(3)正平衡点U0=(0.75,0.875)的焦点(A)及当α=1, β=2, r=1, s=4时, 系统(3)正平衡点U0=(0.5,0.75)的节点(B)Fig.1 Focus of positive equilibrium point U0=(0.75,0.875) for system (3) when α=1, β=2, r=2, s=2 (A), and node of positive equilibrium point U0=(0.5,0.75) for system (3) when α=1, β=2, r=1, s=4 (B)

图2 当τ=0.5时, 系统(3)正平衡点U0=(0.5,0.75)的局部渐近稳定相图Fig.2 Local asymptotic stable phase diagram of positive equilibrium point U0=(0.5,0.75) for system (3) when τ=0.5
由图1可见, 系统(3)的正平衡点U0在τ0处是局部渐近稳定的.由图2可见, 取τ=0.5, 由定理3可知当τ∈[0,τ0)时, 系统(3)的正平衡点U0是局部渐近稳定的.由图3可见, 取τ=2, 当τ>τ0时, 系统(3)的正平衡点U0是不稳定的.

图3 当τ=2时, 系统(3)初值为(u0,v0)=(1,2)时的函数图像(A)和初值为(u0,v0)=(0.8,0.9)时的函数图像(B), 以及对应系统(3)正平衡点U0=(0.5,0.75)不稳定且分支周期解是轨道渐近稳定的相图(C)Fig.3 Function image of initial value (u0,v0)=(1,2) (A) and initial value (u0,v0)=(0.8,0.9) (B) for system (3), and corresponding phase diagram (C) of positive equilibrium point U0=(0.5,0.75) for system (3) unstable and orbit asymptotic stability of branch periodic solutions when τ=2

