基于出行时段选择的高速公路通行费率研究

卢睿彬，严 凌，蔡近近

（上海理工大学 管理学院，上海 200093）

0 引言

近年来，有很多学者对分时段制定票价问题进行了研究。邹庆茹，等建立了以运力运量匹配度最大化为目标的峰前折扣定价模型，对比实际方案，发现相比于提高折扣比例，推迟折扣截止时间可以更为有效地转移高峰客流量，提高疏解效率。张桢桦细分旅客类型，划分出铁路客流的峰谷时段，建立各类旅客运输方式选择的时间价值模型，设计算法求解出各个时段的票价，通过分时定价调节各个时段的客流量。根据小时客流量分布特点，划分出合理的时段是分时段差异化收费的首要条件。刘普寅，等提出可以用偏小型模糊分布刻划偏向小的一方的模糊现象，用偏大型模糊分布刻画偏向大的一方的模糊现象，并将该理论应用于实际算例，分别计算出各个时段的峰、谷拟合度，对时段进行划分。Ralf Borndörfer，等提出用博弈论的方法来提高高速公路网收费效率的策略，用交通流表示用户决策，通过混合整数规划寻找Stackelberg 博弈的纳什均衡解。胡文君，等提出路网设计过程是路网管理者与用户之间Stackelberg博弈的过程，双层规划模型能很好地对这个过程进行刻画。陈建华，等提出出行者广义出行费用的基本函数表达式，对铁路客票价格进行优化。孙朝苑提出公路、铁路的票价制定应由经济、时间、舒适性因素组成的服务特性决定。R.L.Tobin提出了灵敏度分析算法，可有效地求解双层规划模型。

2021年6月，交通运输部、国家发展改革委、财政部联合印发了《全面推广高速公路差异化收费实施方案》，提出各地应在充分考虑本地公路网结构及运行特点的基础上，选择合适的差异化收费方案，全面推广差异化收费，可以从分路段、分车型、分时段、分出入口、分方向、分支付方式角度进行差异化收费。本文对高速公路实行差异化收费进行研究，考虑影响出行者出行时段选择的相关因素，将这些因素加入到现有的出行者效用函数中，建立以高速公路运营方为决策者的上层模型，以出行者为决策者的下层模型，用灵敏度分析算法对模型进行求解，迭代计算出高速公路分时段通行费率，从而对高速公路客流起到有效的均衡引导作用。

1 问题提出

1.1 问题描述

高速公路的交通量时变图一般呈马鞍形，在上、下午各有一个出行高峰，高峰时段较大的车流量会使高速公路部分路段出现缓行及拥堵情况，谷时、平时车流量较少，造成高速公路运能资源浪费，对高速公路划分时段制定合理的通行费率研究,具有显著的现实意义。本文中，高速公路运营方与高速公路出行者之间存在Stackelberg博弈，高速公路运营方制定出分时段的通行费率，出行者做出相应的出行选择，高速公路运营方会依据出行者做出的出行选择调整通行费率，出行者按照调整后的通行费率重新做出出行选择，反复这个过程，直到得出一个相对均衡的结果。建立双层规划模型模拟这个过程，高速公路运营方为上层模型的决策者，出行者为下层模型的决策者。本文根据交通量的时间分布特性，制定与之相适应的分时段通行费率，运用价格杠杆使高速公路出行高峰时段拥堵的客流得到有效转移，从而使高速公路网的交通量分布更加均衡，提高路网运行整体效率。

1.2 问题假设

本文假设条件如下：

（1）出行者出行时段选择受到出行价格因素、出行时间因素、出行舒适安全度综合因素的影响；

（2）高速公路运营方的决策变量是分时段的通行费率，出行者的决策变量是各时段与通行费率相对应的客流量；

（3）分时段的通行费率对各时段的出行客流量起到均衡调节作用，但不改变每天的出行总客流量。

1.3 符号说明

本文所用符号说明见表1。

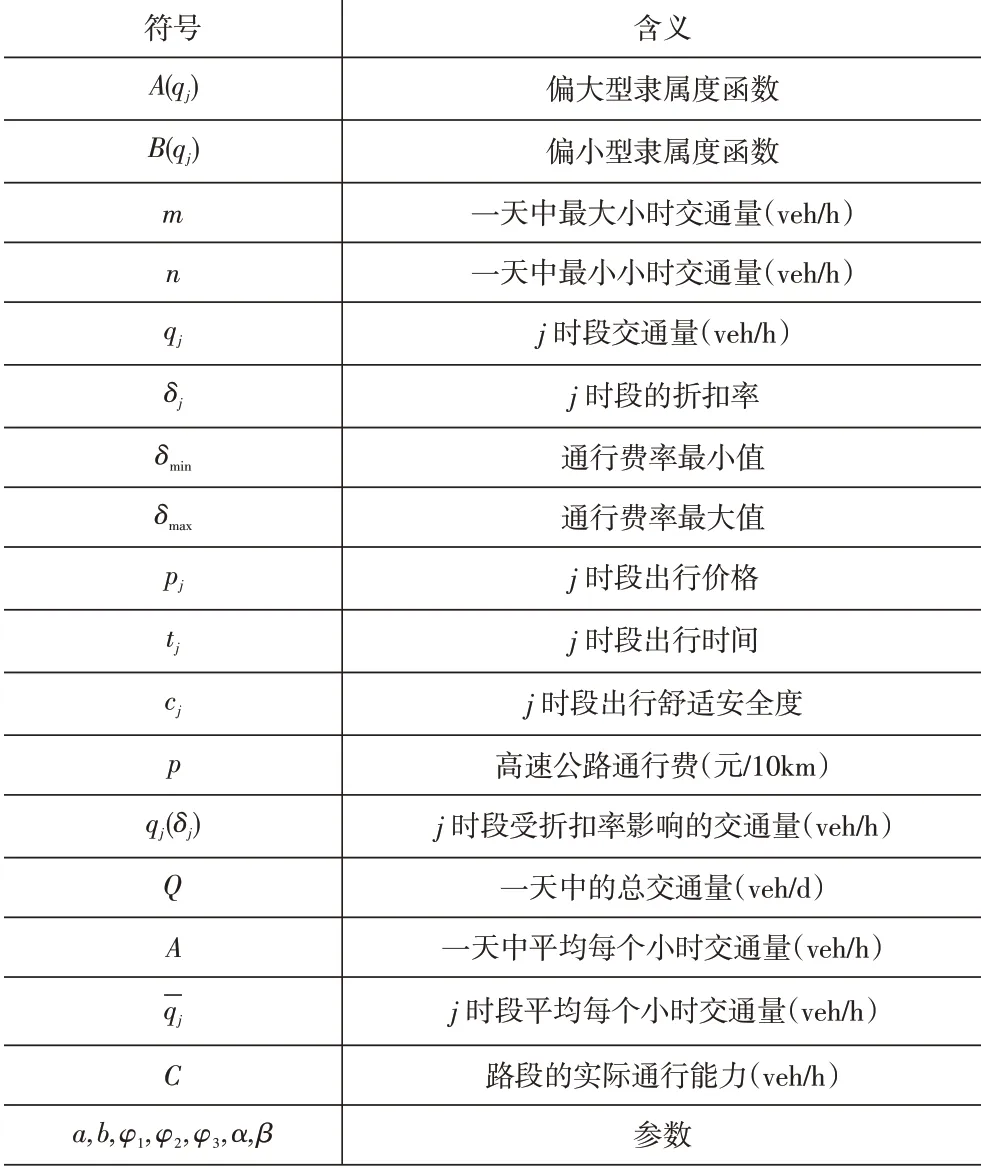
表1 符号说明

2 时段划分

高速公路上一天的交通量在不同时段有着较大的差异，将高速公路按其交通量特征划分出不同时段，并制定出对应的合理通行费率，可以有效地对客流起到均衡作用。本文运用模糊数学中的隶属度函数，用偏大型隶属度函数计算出每个小时交通量的峰拟合度，用偏小型隶属度函数计算出每个小时交通量的谷拟合度，据此将该小时确定为或峰、或平、或谷时段，并进行时段划分。

3 建立双层规划模型

为制定合理的分时段通行费率，建立双层规划模型，上层决策者为高速公路运营方，下层决策者为高速公路出行者。上层模型的决策变量是分时段的折扣率，目标函数是制定合理的分时段折扣率，使高速公路运营方收益最大化；下层模型的决策变量是分时段通行费率下的客流量，目标函数是在假定当天高速公路总出行量不变且为正的条件下，使考虑高速公路出行者出行价格因素、出行时间因素、出行舒适安全度综合因素的广义出行费用最小化。

3.1 上层模型

上层模型以在合理的通行费率区间内，高速公路运营方利益最大化为目标函数。高速公路运营方利益用各时段通行费用与该时段交通量乘积之和来表示。

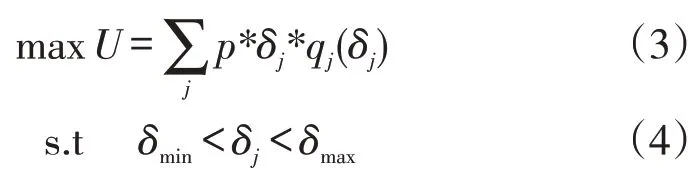
3.2 下层模型

用幂函数表示广义出行费用函数。

其中,为待定参数，分别取2,0.4；V为效用函数。通常高速公路出行者的出行效用与出行价格因素、出行时间因素、出行舒适安全度综合因素有关，这些因素会带来出行负效用。本文将高速公路出行效用表示为：

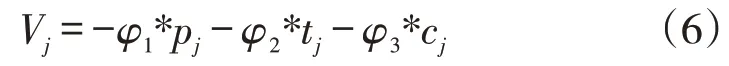
本文用某时段通行费率下的通行费用表示该时段的出行价格因素，用某天交通量的小时均值与某时段交通量的小时均值之间的偏差度表示该时段的出行时间因素，用某时段的出行阻抗系数表示该时段的出行舒适安全度综合因素。本文中时段的出行价格因素、出行时间因素、出行舒适安全度综合因素分别表示如下：

综上所述，下层模型为：

4 基于灵敏度分析方法的启发式算法

4.1 算法原理

运用灵敏度分析法可以求出变分不等式对其中扰动项的导数，本文假定这个扰动项是各时段的出行价格因素，即分时段的通行费率，并且假设各时段的出行时间因素、出行舒适安全度综合因素保持不变。通过灵敏度分析法得出各个时段的高速公路客流量对通行费率的导数关系，用泰勒展开式得出反应函数q()的线性表达式，从而求解双层规划问题。

下层模型通行费率与客流量的均衡配流模型，用变分不等式表示如下：

在OD对w间，存在：

q()是下层模型的均衡解。变分不等式在=1时，即各时段通行费率相同时，存在唯一的q()，在=1时有解的必要条件为：

Λ是OD对间通行费率与对应客流量之间的关联矩阵，是下层模型中等式约束的Lagrangian乘子向量。令()[q(),μ()]，用J()表示式（17）和式（18）对于[q(),μ()]的Jacobian 矩阵，J()表示式（17）和式（18）对于的Jacobian矩阵，则有如下结果：

4.2 算法步骤

该算法计算步骤为：

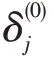
第2步：计算出下层模型的Jacobian矩阵J()和J()，将客流量值代入Jacobian矩阵J()中，并根据式（19）计算出∇y()，得到客流量对通行费率的导数值；

5 算例分析

本算例选取江苏省某高速公路断面逐小时交通量为研究对象，首先，计算每个小时交通量的峰拟合度与谷拟合度，将出行者出行时间划分成若干时段；其次，标定各个时段的出行价格因素，计算各个时段的出行时间因素、出行舒适安全度综合因素，并代入模型中；最后，结合灵敏度分析算法进行计算，得出各个时段的通行费率与相应的客流量。以期通过制定合理的分时段通行费率，达到引导出行者错峰出行，调节客流量的效用。

5.1 数据输入

该段高速公路的交通量时变图为M形，有明显的波峰波谷，高峰时段客流量较大，有时会出现拥堵情况。交通量时变图如图1所示。

图1 江苏省某高速公路断面逐小时交通量图

5.2 实验方案

计算出每个小时的峰、谷拟合度，以70%为分割点，若峰拟合度大于70%，则该时段为峰时段；若峰拟合度在30%-70%之间，则该时段为平时段；若峰拟合度小于30%，则该时段为谷时段。一天被划分为7个时段，根据前文的分析，相关计算结果见表2。

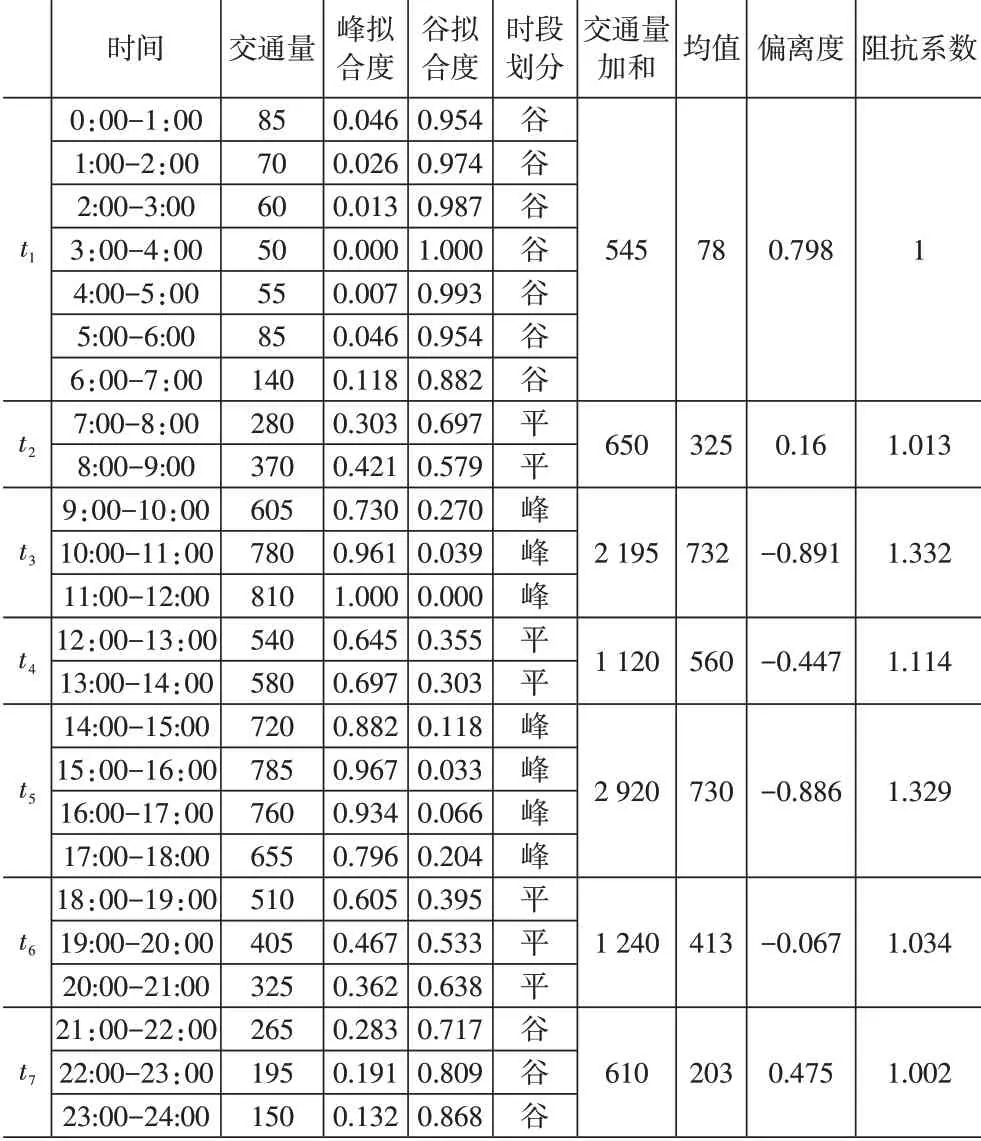
表2 各时段交通量、峰谷拟合度、偏离度、阻抗系数

出行价格因素、出行时间因素、出行舒适安全度综合因素所占权重分别为：0.159 6、0.669 1、0.171 3。在本算例中，取1.3，因为时段为夜间时段，对于高速公路运营方而言，管理运营较其他时段难度稍大，对于出行者而言，便利性较低，所以t时段的取0.8，其他时段取0.7。取0.15，取4，取5元/万km，取600辆/h。

为模拟初始状态，令各时段的通行费率都为1。将权重扩大1倍、5倍、10倍、15倍、20倍、25倍、30倍、35倍、40倍，用MATLAB软件分别计算出各时段的客流量。将各时段计算得出的客流量与实际客流量之间差值的绝对值加总，记为。计算结果见表3。

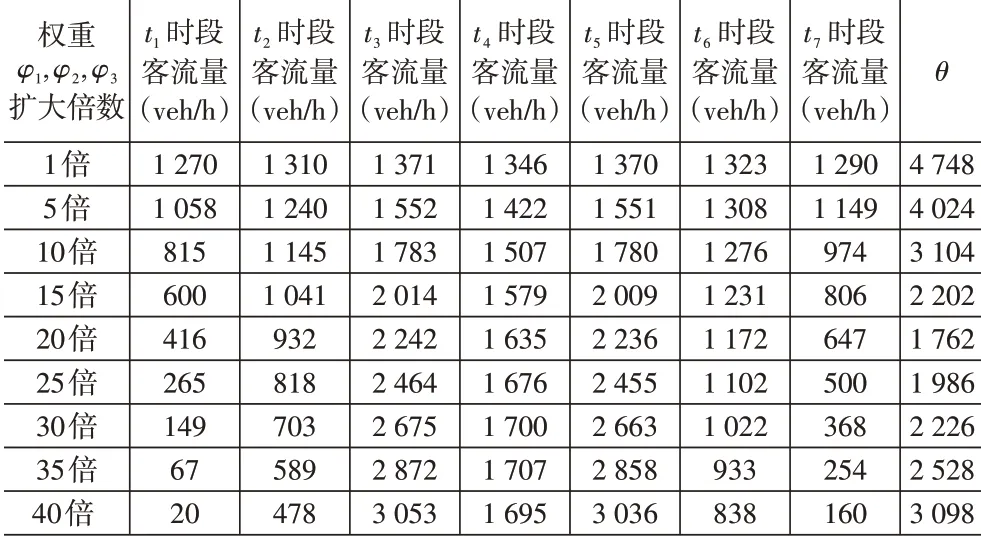
表3 权重φ1,φ2,φ3 扩大后的各时段客流量

值在一定程度上可以反映出模型的拟合效果，由表3可知，权重、、扩大20倍后值最小，故本文将权重、、扩大20倍。

将参数取值代入双层规划模型中，本算例上层模型为：

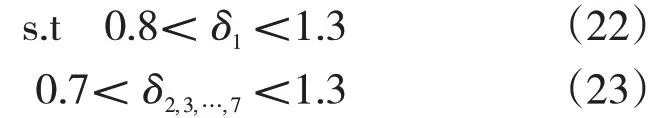
下层模型为：

高速公路运营方给定各时段的通行费率，出行者做出对应的出行决策，运营方会根据出行者的出行决策调整通行费率，同时出行者会根据新的通行费率做出新的决策。运营方给定的各时段初始通行费率都为1，将其代入下层模型，得出各时段对应的客流量，运用前文所述灵敏度分析算法确定高速公路各时段客流量对通行费率的导数关系，通过泰勒展开式计算出高速公路各个时段的客流量与其对应通行费率的反应函数，将其代入上层模型，计算得出第1步的分时段通行费率，再将其代入下层模型，得出与之对应的分时段客流量。重复这个迭代过程，直到运营方给出的通行费率与上一轮相比差值在一个可接受范围内，即停止迭代计算。经过4 步迭代，最终得到误差值＜0.005的分时段通行费率，见表4。

表4 迭代计算结果

5.3 结果分析

经过4步迭代，可得各时段的通行费率分别为0.8、0.944 9、1.250 1、1.123 9、1.248 2、1.012 2、0.851 9。通过计算可知，制定分时段通行费率前，上层规划模型的目标函数值为46 400元，下层规划模型中出行者广义费用为364.38元；将第4步迭代计算结果代入双层规划模型中，可得分时段通行费率下，上层规划模型目标函数值为50 511.4元，下层规划模型中出行者广义费用为375.2元。对比制定分时段通行费率前后的客流量，可知对不同时段按相应的通行费率征收费用，可以在满足上层规划模型高速公路运营方利益最大化目标，考虑下层规划模型出行者广义费用最小化目标下，有效地转移高峰时段客流量，缓解了该高速公路路段早晚高峰的拥堵情况，同时，更好地发挥了高速公路谷时、平时的运行效能，对高速公路交通流起到了显著的均衡作用，如图2所示。

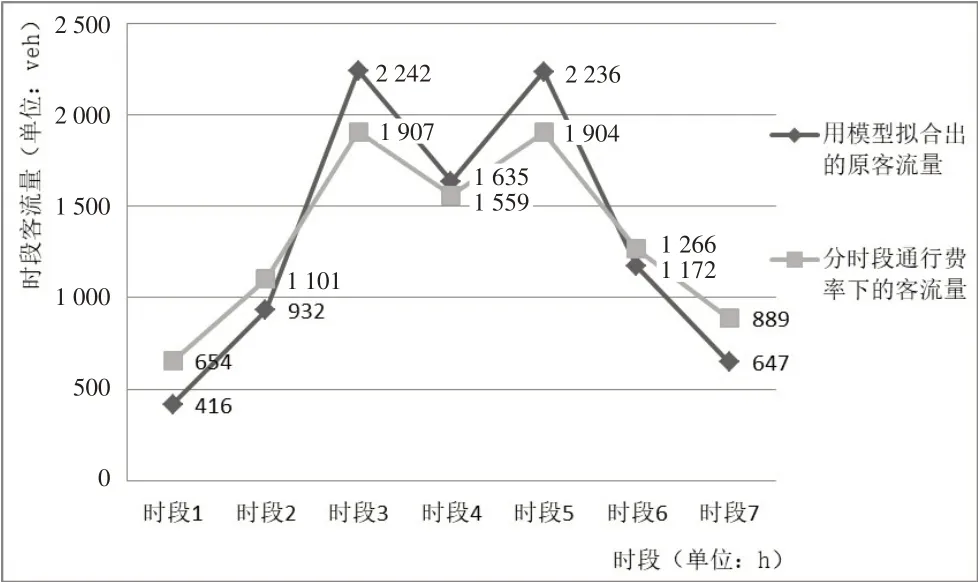
图2 制定分时段通行费率前后客流量对比图

6 结语

制定合理的分时段通行费率是转移高峰时段客流量的有效手段之一，本文首先运用模糊数学将出行者出行时段划分为峰、平、谷时段；其次，构建了双层规划模型，上层模型以高速公路运营方收益最大化为目标，下层模型以出行者广义出行费用最小化为目标，在现有研究基础上构建了考虑高速公路出行者出行价格因素、出行时间因素、出行舒适安全度综合因素的广义出行费用函数；最后，运用基于灵敏度分析方法的启发式算法求解，得到各个时段的差异化通行费率以及相应的客流量分布，并通过算例分析验证了模型算法的有效性。研究结果表明，分时段的通行费率可以有效地对交通流起到削峰填谷的作用，在考虑高速公路运营方与出行者双方利益的条件下，使高速公路交通量得以均衡。