运用画图表征，提升学生几何直观能力

■天津市西青区王稳庄镇中心小学 张庆江

画图表征是数学教师教学的一种重要手段。它凭借图形的直观性，将抽象的数学语言与直观的图形语言有机结合，引导学生根据自己的需要画出不同的图，使数学语言合情转换成几何直观图形，达到以形助数、让数学在学生的眼中变得简洁而丰富的目的。

一、运用画图表征，使学生“理清法明”，实现算理与算法的无痕对接

在计算教学中，部分教师只借助语言表征进行枯燥的讲解，往往造成学生“理不清，法不明，能难成”，为了更好地使学生明理懂法，在教学中可以让学生借助点子图、方格图、线段图等多种画图表征直观地呈现计算的过程，将理的抽象与法的直观巧妙地结合。

【“分数乘分数”教学片段】

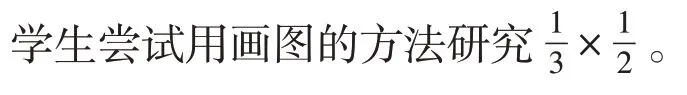
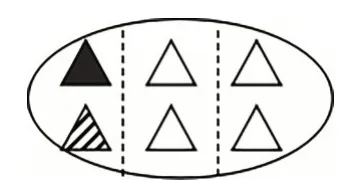
（图一）

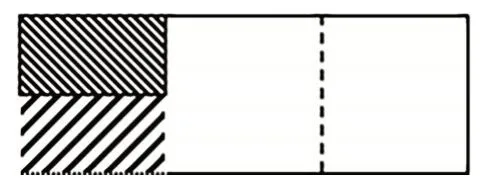
（图二）

（图三）

学生总结分数乘分数的计算方法。

虽然我们画的图式不同，但我们能根据不同的图式表征来理解算理。学生经历了“分了再分，取了再取”的数学活动，丰富对分数乘分数的理与法的直观认识。通过多种画图表征，学生在思想碰撞过程中，一步步体会、领悟分数乘分数的算理，进而概括总结出分数乘分数的算法，实现了“理”与“法”的无痕对接。

二、运用画图表征，展示思考过程和解题方法之妙，培养学生的创新意识

画图表征是我们解决问题中常用的一种思考策略，也是容易操作的一种策略。在数学教学中，运用画图表征的目的不仅仅是帮助学生解决某些数学问题、提高能力，更重要的是使学生真正学会自主学习，养成“数学思考”的习惯。

【“集合”教学片段】

教学三年级《集合》时，在学生初步认知集合中的重复现象后，教师是这样进行练习设计的：先让学生独立思考，自主画图去分析解决，如果同样是4个语文状元和5个数学状元，有2个学生既获得了语文状元又获得了数学状元，总人数该是多少？学生列出多种算式后，教师没有简单地重复书上的练习，而是让学生继续思考：同样是4个语文状元和5个数学状元，除了8人、7人之外，还有其他的可能吗？选一种可能画图表示并列出算式？学生充分运用画图表征，创作出了多种超乎寻常的可能。

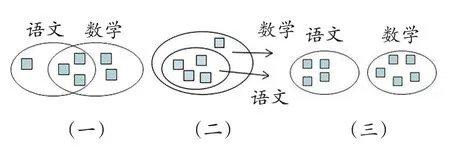
看着学生的作品，听着学生精彩的回答，这其中包含着学生思维能力的发展，我想：学生为什么会有这样的认识和回答，是因为学生有了前面知识的积淀，有了几何直观的引领，使他们不仅正确认识到集合中的几种重复现象，还想到了交集为空和包含的存在性。画图表征的运用，不但有利于帮助学生理清数量关系，还能提高学生的思维能力和解决问题的能力，学生的数学素养得以提高。

三、借助几何直观，揭示数学知识之间隐含的规律，激发学生探究的热情

【“图形中的规律”教学片段】

上课伊始，教师引导学生动手用5根小棒摆出2个三角形，要求学生用算式将摆的过程写出来，教师并板书3+2，摆3个、4个、5个分别用了多少根小棒，可以画一画，写一写，并将摆的过程用算式表示出来。学生研究后汇报出3个、4个、5个三角形，分别用了3+2×2、3+2×3、3+2×4根小棒，教师追问这三个算式的意思。教师继续问：如果继续摆下去，摆10个这样的三角形呢？怎样列式计算呢？学生有了前面的体验很快答出3+2×9，之后教师抛出：摆100个三角形需要多少根？学生回答3+2×99，教师再问：99怎么来的，为什么要用100减1，由于学生经历了3个、4个、5个、10个的研究过程，所以学生对于3+2×99这个式子很容易解释，因为有了这些知识的铺垫，之后教师再次提高思维难度让学生运用一个数量关系式表示出来。在教师多层次的引导下，学生借助直观图，很自然地概括出三角形个数、摆成的图形与小棒的根数三者之间的关系，而这个规律的得出是依托于前面大量的以图操作、以图观察的活动，归纳的过程在不断地帮助学生去思考，去完善，去总结，去归纳，逐步逼近数学本质。在归纳过程中，教师向学生渗透了数学的学习方法——化繁为简、操作、分析归纳、得出规律，让学生在经历中有感悟，有思考，有成果，只有这样的“直观”才能化繁为简，在经历中习得新知，在经历中揭示数学规律。

四、运用画图表征，凸现数学本质，渗透数学思想

《数学课程标准》明确提出了把数学的基本思想作为总体的教学目标之一，数学思想方法不像数学知识那样显现在教材上，而是隐含在教材中，教师选择适合内容，去挖掘、提炼数学思想方法，借助画图表征的直观性可以引导学生理解掌握数学思想，提高学生解决问题的能力。

【“分数的基本性质”教学片段】

这样精彩的解释，说明数学思想已经根植于学生心中，最后教师总结：分数的分子和分母同时除以几，相当于每几份合成一份；分数的分子和分母同时乘几，相当于每一份平均分成几份。由直观到抽象，两次活动紧紧抓住分数基本性质的本质：变中有不变的思想，让学生去体会、去思考、去感悟，分数的基本性质自然而然地呼之欲出，由于学生有了亲身经历，所以概括分数的基本性质水到渠成。正是通过不断地画图、析图、用图，学生已有的经验被激活并融入到新知的学习中来，并展开了深入的数学思考。开放的环节最终赢得了丰富的课堂回报，学生在活动中理解了分数基本性质的本质，同时数学思想也牢牢印在学生心中。

通过丰富画图形式，把抽象的数学语言转化为形象、生动的几何图形，可以打开学生思维，起到化难为易、化繁为简、化隐为显的作用，使学生爱上数学、乐学数学，会用数学。因此在我们的课堂上，更应借助画图表征，让学生的双手操作起来，让学生的思维活跃起来，让学生的几何直观能力真正得以提升。