入流含油率及油相物性对紧凑型重力分离器内分界层高度影响的数值研究

王宗勇，林茹亭，李权，李航，刘家栋

（沈阳化工大学 机械与动力工程学院，辽宁 沈阳 110020）

随着陆地油田储油量的日益减少，我国及世界多国开发了大量海上油田。由于海上油田平台的空间十分有限，其上的操作设备须更加小巧、紧凑。要在较小的分离器容积即较短的停留时间下，达到工艺要求的分离效果，就需要分离器具有比普通分离器更高的分离效率[1-2]。对于这种紧凑型重力油水分离器的分离性能研究及结构优化设计是当前乃至今后一段时期的一项重要任务。

用于油田初步油水分离的重力式分离器，其入流含油率和物性会产生一定程度的变化，这两方面变化直接影响分离器内的流动特性以及油水分界层高度[3-4]，进而影响分离器的分离性能。其中，分界层高度对于普通分离器影响相对较小，但对于紧凑型管式分离器影响较为明显，其会使分离器的有效分离容积占比发生明显变化。王国栋[5]等通过实验研究分析了油层厚度对于油相停留时间的影响，当油层厚度相同时，进口含油率越小，油相的停留时间越少。周晓君[6]等通过理论研究推算出油相在油水两相混合区域的运动方程，得出了油水两相在其内部的流动规律。DC Drown[7]等通过实验研究了油滴在油水两相混合区域的流动聚结过程，发现聚结速率不仅取决于静态环境中的流体性质，还取决于液滴之间的动力黏度。SUN Zhiqian[8]等通过实验研究，分析了油滴在分离器内不同区域的上升行为，实验结果表明，在入口区域油水混合物紊流较大，油滴上升速度与其他区域相比较慢。陆耀军[9]等,对油滴在连续相中的受力,运动和轨迹进行了较为系统的分析，并采用Stokes 公式进行液滴的受力计算，揭示了重力式油水分离器的分离规律。综上所述可以发现，油相的物性、油滴的运动都会对分离器内的各个区域厚度产生影响，进而影响分离器的分离效率。

本文通过数值模拟方法对进口油含率以及油相物性（黏度，粒径）进行分析，探究其与分界层高度之间的关系，旨在为管式分离器的结构设计和工程应用提供技术支持。

1 数值模拟

1.1 分界层及其高度定义

为了清晰表达油水两相在分离器内的分布状态，本文针对分离器轴向中间截面按照油相浓度沿着竖直方向变化情况，将分离器流动截面分成三个区域：油层，即高浓度油相区域，其油相体积分数CO>90%；分界层，即油水两相混合区域,其油相体积分数10%≤CO≤90%；水层，即高浓度水相区域，其含油体积分数CO<10%。为了便于后面的分析说明，将油层和分界层的分界面称为油相界面；分界层和水层的分界面称为水相界面。各区域名称及分布情况如图1所示。

油水两相在分离过程中，由于受到分离器管壁及内构件的影响，油相界面和水相界面形状通常为一曲面（线），致使分界层在不同横向位置所对应的高度产生变化，为此需要定义一个平均高度（h）作为分析过程的标定高度，该高度就是油相界面曲线竖直位置平均值与水相界面曲线竖直位置平均值之差，也就是图1中上下两条红线之间的距离。

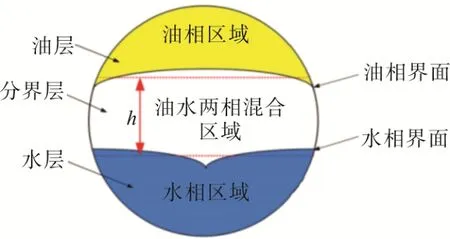
图1 分界层及其高度示意图

1.2 几何模型

本文所研究的紧凑型重力分离器采用圆管作为筒体，两端选用椭圆封头。油水混合液在封头中心采用轴向入口，油相出口位于封头过渡区域沿轴向出流，水相出口位于筒体底部沿径向出流。分离器内部设置整流构件和聚结构件，其中整流构件采用圆形挡板，聚结构件采用正V 形聚结板。分离器（包括内构件）结构和参数分别如图2和表1所示。

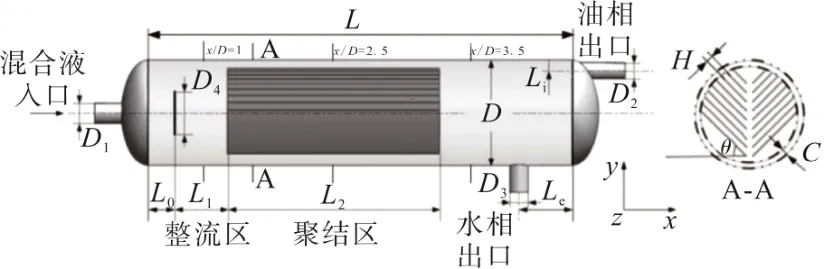
图2 紧凑型重力分离器模型图

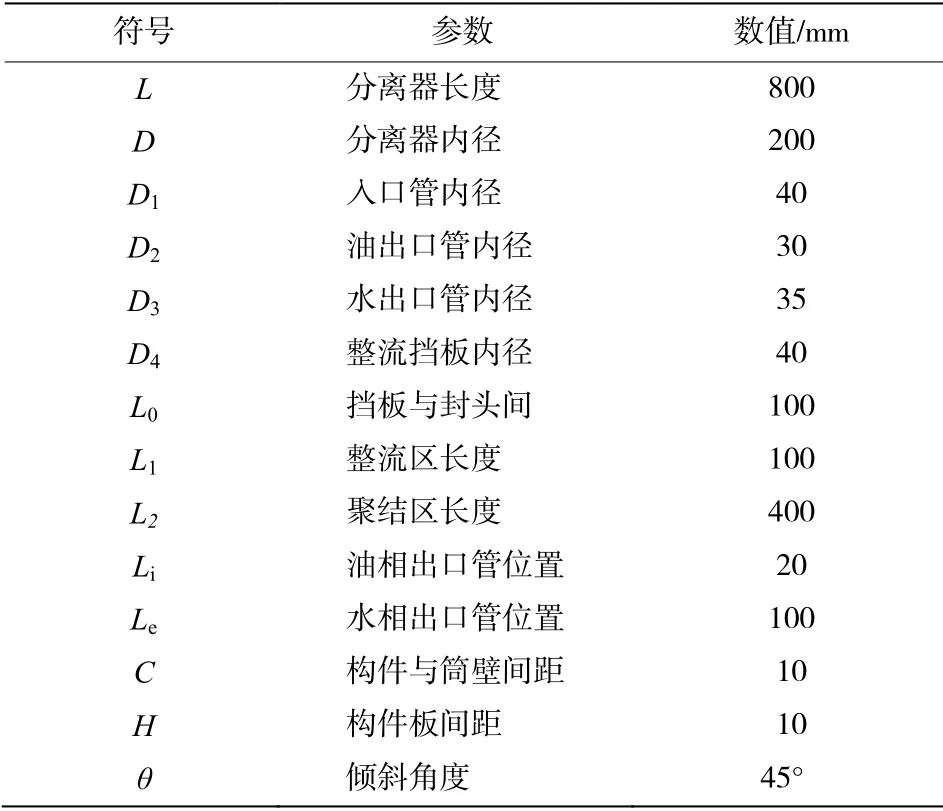
表1 紧凑型重力分离器结构参数表

1.3 数值模拟及边界条件

本文通过Fluent 软件对分离器进行模拟研究，采用Standardκ-ε湍流模型与Mixture 多相流方程对油水两相流进行计算，模拟中油水两相为不可压缩流体，流体流动过程中无热量交换。压力和速度耦合采用SIMPLEC 算法，体积分数差分格式为QUICK,压力差分格式为PRESTO，入口边界条件为速度入口，工作介质采用油和水混合得到，其中水相介质密度为998.2 kg·m3，黏度为1.003 mPa·s；油相介质密度为780 kg·m3，黏度选取0.4～5.4 mPa·s，油为分散相。油水两相出口均设置为自由流。

1.4 网格无关性检验

网格质量影响模拟的运行速度以及计算结果，为了消除网格数量对模拟带来的影响，确保计算结果的稳定性和准确性，本文对各种参数下的分离过程进行了网格无关性检验。利用ICEM 软件对仿真模型进行非结构化网格（四面体网格）划分，通过调整最大网格尺寸，划分多组网格，利用分离器中横截面（x/L=0.312 5）上速度的相对标准偏差[10]（速度不均匀度cv）与网格数量的关系，来确定最优的网格尺寸。速度不均匀度越小，代表分离器流动均匀性越好，油水分离能力越强，利用该参数作为网格无关性检验的评价指标较为合理。速度不均匀度方程为：

式中：n—采样点个数；

vj—第j点的采样速度；

—采样点的平均速度。

本文的网格尺寸与速度不均匀度关系如图3所示，从图中可以看出，当网格数量<300 W 时，随着网格数量的增加，速度不均匀度逐渐渐下降，表明网格数量与计算结果存在着较大的相关性，当网格数量增加到300 W 以后时，速度不均匀度基本趋于定值，说明达到该网格数量后，网格数量对于计算结果已无影响，在综合权衡计算时间的前提下，本文采用的网格数量均保持在300 W 以上。

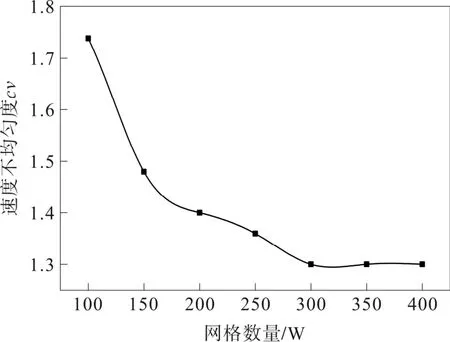
图3 速度不均匀度与网格数量关系

2 结果与讨论

由Newton 第二定律和Stokes 定律可知油滴在油水混合区域中的运动轨迹方程为：

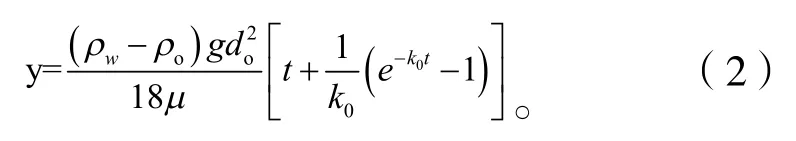
式中:ρw、ρo—分别为水、油的密度；

do—油滴粒径；

μ—油水混合液的动力黏度。

从文献[6]中得出混合液黏度与油水两相黏度的关系为：

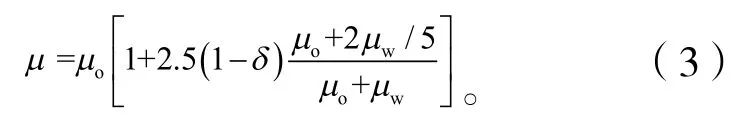
式中：μw—水的动力黏度；

μo—油的动力黏度；

δ—分离器内含水量。

由以上两式中可以看出，油水两相黏度及油滴粒径均会影响油滴在油水混合层即分界层中的运动轨迹，但对于分界层高度却不能直接得到。分界层高度对于小直径的管式分离器而言影响明显，其不仅决定了分离器的有效分离空间，也决定了油滴上浮时间，进而影响到分离器的处理能力和分离效率。因此，本文拟通过改变入流含油率、油相黏度、油滴粒径三方面因素对分界层高度变化规律进行分析。

2.1 入流含油率对分界层高度的影响

入流含油率（Vo）决定了分离器内油水两相的比例，进而影响到油水混合液的物性，从而对分界层高度产生影响，最终影响分离器的分离性能。为了探究入流含油率对分界层高度变化的影响，本文对Vo=10%和20%的x=500 mm 截面处的浓度云图（入口流速0.2 m·s-1）进行了对比，如图4所示。

图4 油相浓度云图

由图4可以明显看出油相界面呈现凹形，水相界面呈现凸形，形成这种界面形状的主要原因是流体通过聚结构件时，油滴在聚结板表面进行聚结，当油相的浮力大于自身重力以及聚结板的摩擦阻力，通过聚结斜板斜向上浮升，在圆筒形壁面的作用下大粒径油滴向中间靠拢并继续上浮，而分界层区域的水滴沿斜板斜向下向中间汇合沉降，从而使油、水相界面呈现凹、凸面形状。对比（a）和（b）子图中油相区域可以发现，入流含油率增加，油相区域明显增大，这是流体流动连续性决定的，同时也与油水两相之间的相互作用有个，即分离器内部油含量充足，油滴之间相互碰撞、聚结概率增大，大粒径油滴可以较为快速地到达分离器上层，进而增大了油相区域。此外，入流含油率增大，相应的分界层高度也明显增大，存在较为明显的油相浓度分层现象，造成这种现象是因为在分界层区域中，油相浓度产生显著变化，由上至下水相由分散相变为连续相。为了准确探究入流含油率对分界层高度（h）变化的影响，本文针对不同截面处（x/D=1，2.5 和3.5）的不同含油率下分界面进行了研究，所取得三个截面分别位于聚结构件前、中、后三个轴向位置，结果如图5所示。

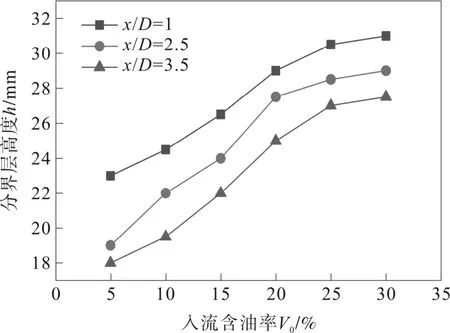
图5 分界层高度与入流含油率关系

由图5可知，三个截面处的分界层高度随入流含油率变化规律是相同的，均随着含油率的提高而增大，在体积分数5%～20%范围内分界层高度增加快速，与含油率基本呈现线性关系，而在20%以后的浓度范围内分界层高度增加缓慢。这种现象说明含油率提高增大了分离过程中油水之间接触的比例，同时也增大油滴之间碰撞聚结的概率，前者使油水混合液的密度减小、黏度增大，导致油滴浮升速度减慢，分界层高达增大；而后者可以增大油滴可以提升浮升速度，对于分界层厚度减薄具有一定促进作用，但显然该作用与混合物物性改变相比是比较弱的，仅在较高入流含油率（>20%）下其作用才变得明显，分界层增幅变得比较缓慢。

对比图5中的三条曲线可知，随着油水混合液轴向流动距离的增长，分界层高度在逐渐减小，形成这种规律的原因有两个：一是随着流动距离的增加，意味着油滴在油水混合区即分界层内的停留时间在增大，更多的较小粒径油滴通过油水分界面进入油层，导致分界层厚度逐渐减薄；二是斜板聚结构件对于分界层减薄起到了促进作用，小油滴在聚结板下表面聚结并斜向上流动，在分离器边壁汇聚后再向上浮升，减小了油水逆向流动时相互之间的影响，促进了分界层的逐渐减薄。

2.2 油相黏度对分界层高度的影响

油相动力黏度（μ）代表着油滴之间相互的内摩擦力大小，由公式2 可知，油相动力黏度的改变会引起油水混合液动力黏度的变化，使油滴在油水混合层中运动速度和轨迹发生改变。为了揭示油相动力黏度对分界层高度的影响规律，本文选用6 种黏度对入流含油率20%的紧凑型重力分离器进行了模拟计算，边界条件与前述保持一致。

图6显示了不同油相动力黏度与分界层高度的变化关系，从中可以看出：随着油相动力黏度的增大，分界层高度随之减薄，在较小的黏度范围内（0.4≤μ≤2.4），分界层高度下降快速，而在2.4≤μ≤5.4 黏度范围内下降缓慢，在两个黏度范围均按照相应的线性规律降低。形成这种现象的根本原因是：黏度增大提高了油滴之间聚结的能力，随着流动的进行液滴粒径会得到明显增大，尽管黏度增大会提高混合液的黏度，但对于油滴浮升速度而言，其小于与油滴粒径平方成正比而与混合液黏度一次方成反比，最终的浮升得到显著提升，进而导致分界层高度减薄。当油相黏度较高时，油水混合液黏度的影响变得比较显著，而对于油滴之间的聚结作用变得不如以前明显，所以导致较高浓度范围内分界层高度增加变缓。不同截面位置的分界层高度仍旧体现出与2.1 节相同的规律和原因。

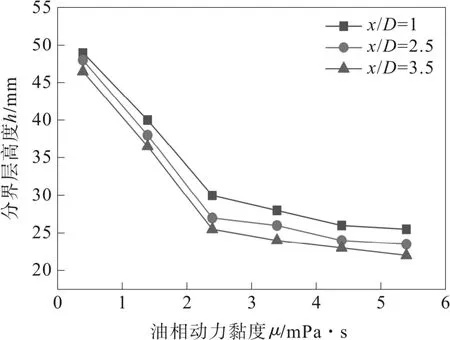
图6 分界层高度与动力黏度关系

2.3 油滴粒径对分界层高度的影响

为了研究油滴粒径对分界层高度的影响，从油相粒径30 μm 为起点，以30 μm 为增量等间隔选取6 种不同大小的油相粒径，对分离器内三处截面（位置与上述保持一致）出的分界层进行分析。

图7为不同油相粒径与分界层关系图，从中可以看出：三个截面处的分界层高度呈现相同的规律，均随着油滴粒径（do）的增大而变小，并且在30 μm≤do≤120 μm 范围时下降迅速，而在120 μm≤do≤180 μm 范围时下降缓慢。这种现象可以通过Stokes 浮升速度公式得到解释，油滴粒径增大显著增加的浮升速度，进而导致油水得到快速分离，相应的油水分界层高度减小。但当油滴粒径达到一定程度后，部分油滴在黏度剪切力以及斜板入口剪切作用下容易破碎变差小油滴，进而减缓了分界层高度增加速度，导致较高粒径范围内分界层高度反而增加放缓。

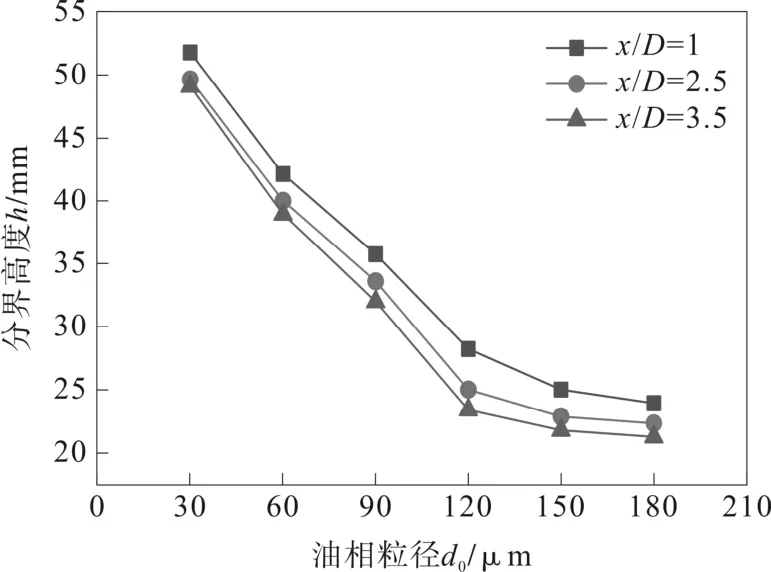
图7 分界层高度与油相粒径关系

3 结 论

本文采用CFD 方法对紧凑型重力分离器进行模拟研究，分析了入流含油率以及油相物性对分界层高度的影响，得到以下结论：

1）分界层高度随着入流含油率的增加而增大，在入流含油率达到20%以后时分界层高度增速放缓。

2）随着油相黏度和油滴粒径的增大，分界层高度均之减小，说明在本文所研究的黏度和粒径范围内，这两个参数的增大对于油水分离越有利。

3）分界层高度随着油水混合液轴向流动长度的增加而减小，表明分界层高度与分离效果之间存在必然的联系，具体关系有待进一步研究。