团簇Co3FeP光谱的预测分析

毛智龙,方志刚,侯欠欠,王 倩,许 友,宋静丽

(辽宁科技大学化学工程学院,辽宁 鞍山 114051)

0 引言

随着科技的发展，各种新型材料不断涌现,其中过渡金属磷化物(Transition-metal phosphides,TMPs)作为一种用途广泛、性能优异的材料逐渐被研究人员关注.在过渡金属磷化物中，非晶态合金Co-Fe-P 3元体系由于具有优异的催化性能[1-3]和磁学性能[4]等因而脱颖而出.

在催化水解领域中，研究人员为满足不同需求，制造出不同结构类型的Co-Fe-P催化剂，并在实验中发现Co-Fe-P的催化性能不仅与贵金属催化剂非常相近[5],而且在某些特定环境的应用中比贵金属催化剂表现出更为优异的催化效果[6-7].Zhang Wenqian等[8]发现由于次磷酸钠诱导的部分磷化可以大大降低纳米片的厚度，促进材料的多晶性质，使更多的活性位点暴露出来，使电子传输更快，所以通过水热法和磷化法相结合制备的超薄无定形CoFeP纳米片具有优异的催化性能[9];同时，Zhang Wenxiu等[10]认为:CoFeP具有优异的催化性能的原因是其多孔的特性和π电子在Fe和Co阳离子间的重新分布;Zhao Changhao等[11]通过对制备的CoFeP/NC进行研究发现:该材料具有优异的催化活性的主要原因是CoFeP纳米球和碳网络的强协同作用不仅可以使电解质和催化剂之间更好地接触，提供大量可用的活性位点，还可以形成一个网络，以提高其耐用性和导电性.此外，S.M. El-Refaei等[12]研究发现,在不同的pH值下CoFeP均具有较高的催化活性.在催化莠去津(atrazine,ATZ)降解中,Zhu Jinglin等[13]发现CoFeP具有较高的催化活性、重复使用性和稳定性，能够活化PMS(peroxymonosulfate,过一硫酸盐)去除水中的ATZ.

除了在催化剂材料领域中的应用外，在磁性材料领域的应用中，研究人员发现非晶态合金Co-Fe-P的多孔中空结构对施加的磁场很敏感[14],并且在室温下具有超顺磁性[15];在电极材料领域的应用中，Zhang Chaoqi等[16]通过对管状CoFeP@CN进行研究后发现:异质结构内电子分布的改变使其在充电/放电过程(包括LiPS相变和Li2S沉积/溶解)中降低了能垒，从而减小多硫化锂的穿梭效应和高能垒对锂硫电池性能的损害.

基于上述内容不难发现,Co-Fe-P是一种优异的新型材料.因此,在相关研究的基础上，对其展开深入研究是十分必要的.现有的研究大多数是宏观实验研究，相关光谱的实验研究鲜见文献报道.因此,本文在B3LYP/def2-tzvp的量子化学水平下,以Co3FeP[17]为局域模型，对Co-Fe-P体系的红外光谱和拉曼光谱进行了研究和预测，以期探明其结构特征和规律，为后续实验提供理论参考.

1 模型与计算方法

1.1 模型设计

以文献[17]中Co0.61Fe0.21P0.16为基础比例模型，为方便后续数据处理及计算将其简化为Co3FeP，并利用拓扑学原理[18-19]得到团簇的初始构型.

1.2 计算方法

利用密度泛函理论[20-21]中B3LYP杂化[22-23]和def2-tzvp基组对所有初始构型在单、三重态下进行全参数优化和频率计算，其中P原子加上极化函数ξP.d=0.55[24].优化收敛条件为最大作用力小于 0.000 45，均方根作用力小于0.000 30，最大位移小于0.001 80，均方根位移小于0.001 20.所有计算均在HP Z440上运用Gaussian09程序完成.

使用洛伦兹函数[24]对计算结果进行处理,并将数据绘成连续的红外光谱图和拉曼光谱图.

2 结果与讨论

2.1 优化构型

在对团簇Co3FeP进行优化计算,在排除虚频和相同构型后，所得优化构型的几何形态为三角双锥(构型1(3))、四棱锥(构型1(1)和构型2(1))和带帽三角锥(构型3(1)).以能量最低的构型1(3)作为能量基准点(设为0 kJ·mol-1),其他构型按照相对能量大小依次排序，其中右上角标表示其自旋多重度,C1表示其对称性(见图1).

1(3)(0 kJ·mol-1) 1(1)(410.84 kJ·mol-1) 2(1)(412.74 kJ·mol-1) 3(1)(584.44 kJ·mol-1)

2.2 红外光谱

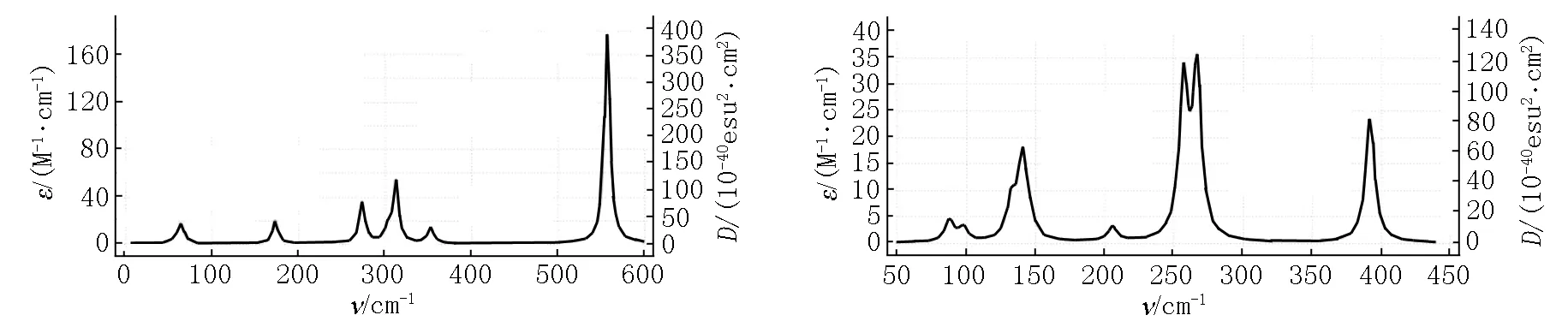
2.2.1 红外光谱图 在物质产生红外活性时需满足如下条件:(i)被吸收的辐射光子具有的能量与在发生振动跃迁时所需的能量相等；(ii)辐射与物质之间有耦合作用，即分子的偶极矩发生改变.由n个原子构成的分子在产生红外活性后，直线型分子有3n-5种振动形式，而非直线型分子有3n-6种振动形式.据此可得,团簇Co3FeP的分子振动形式在理论上应有9种.将所有优化构型的红外光谱计算数据拟合为一条连续的曲线，结果如图2所示.

由图2及相关计算数据可知:构型1(1)有7个振动峰，呈现出两侧大、中间小的趋势，其中最高峰的波数为453.59 cm-1,振动形式为Co1—Co2—P5键和Co2—Fe4—Co3键的面内剪式振动，次高峰的波数为76.03 cm-1,振动形式为Fe4—Co1—P5键和Co2—Co1—Co3键的面内剪式振动；在其他特征峰中，除波数为419.51 cm-1的特征峰峰值与次高峰的相近外，其他峰则相对较小.构型2(1)有6个振动峰，也呈现出两侧大、中间小的趋势，其中最高峰的波数为433.15 cm-1,振动形式为P5—Co1—Co3键和Fe4—Co1—Co2键的面内剪式振动，次高峰的波数为397.22 cm-1,振动形式为Fe1—P5—Co3键的面外扭曲振动，2者的峰值相近.除上述及波数为83.76 cm-1的特征峰较为明显外，其他峰均较小.与构型1(1)同为四棱锥的构型2(1),2者不仅特征峰的分布相似，而且最高峰振动形式相同，这说明在几何构型相似时，红外活性的频率也相似.构型3(1)有6个振动峰，分布趋势为右侧大、中间小且左侧最小，其中最高峰的波数为557.43 cm-1,振动形式为Co1—P5—Co3键和Fe4—P5—Co2键的不对称伸缩振动，次高峰的波数为312.90 cm-1,振动形式为整体变形的弯曲振动，而相比于上述其他单重态构型，构型3(1)的最高峰波数明显大于上述单重态构型最高峰的波数(430.00～460.00 cm-1),即发生了蓝移现象，且振动形式为不对称伸缩振动.由图1可知:在单重态构型中，只有构型3(1)的几何形态为带帽三角锥，这说明构型的几何形态会对其红外活性产生影响.构型1(3)有6个振动峰，特征峰集中分布在两侧及中间，其中最高峰的波数为262.84 cm-1,振动形式为Co1—P5—Co3键的弯曲振动，次高峰的波数为246.57 cm-1,振动形式为Co1—P5—Co3键的对称伸缩振动和Co2—Co3—P5键的面内剪式振动，相比于单重态构型最高峰和次高峰的波数分布情况，三重态构型的波数分布更小、更集中，这说明构型的自旋多重度会对构型的红外活性产生影响.

1(1) 2(1)

3(1) 1(3)

2.2.2 偶极矩 因为物质的红外活性与其偶极矩密切相关，且偶极矩越大，其红外活性越强.为进一步说明各构型偶极矩与红外活性的关系，将优化构型的偶极矩列于表1中.

由表1可知:在单重态构型中，构型1(1)的y轴和z轴对其偶极矩贡献相近，这说明红外活性主要由y轴和z轴提供；构型2(1)的y轴对其偶极矩贡献最大,即y轴是其红外活性的主要来源.同时，构型1(1)和构型2(1)均为四棱锥(Co原子为锥顶原子，其他原子为底面原子)且总偶极矩值相近，这说明几何形态相似的构型其偶极矩相近；对于几何形态不同于构型1(1)和构型2(1)的构型3(1)而言，其总偶极矩值较小且主要由x、y轴贡献，这说明构型3(1)的偶极矩主要由x、y轴贡献,即2者均是其红外活性的主要来源，并且构型几何形态的不同会导致其红外活性有所差异.在三重态构型中，构型1(3)的偶极矩绝大部分由x轴贡献，这说明构型1(3)的红外活性几乎全部来自x轴；同时构型1(3)的总偶极矩远大于单重态构型，这表明构型的自旋多重度会对其偶极矩的大小产生影响，进而对其红外活性产生影响.

表1 团簇Co3FeP各优化构型的偶极矩

2.3 拉曼光谱

2.3.1 拉曼光谱图 拉曼光谱是一种散射光谱，红外光谱与偶极矩有关，而拉曼光谱与诱导偶极矩有着紧密联系，因此拉曼光谱可以作为红外光谱图的补充，进而对物质的结构进行更为深入地了解和阐述.同时，拉曼光谱由于机理的不同，所以其相比于红外光谱拥有如下优势:(i)无需准备样品;(ii)所需样品量少;(iii)覆盖波段区间大;(iv)更适合定量研究.拉曼光谱存在反斯托克斯散射区(波数为负的区域)、瑞利散射区(波数为0的区域)和斯托克斯区(波数为正的区域),但在红外光谱中只有波数为非负的区域.为方便研究，本文将拉曼光谱的反斯托克斯区域略去，只研究其瑞利散射区和斯托克斯区.将拉曼光谱图进行拟合绘制，结果如图3所示.

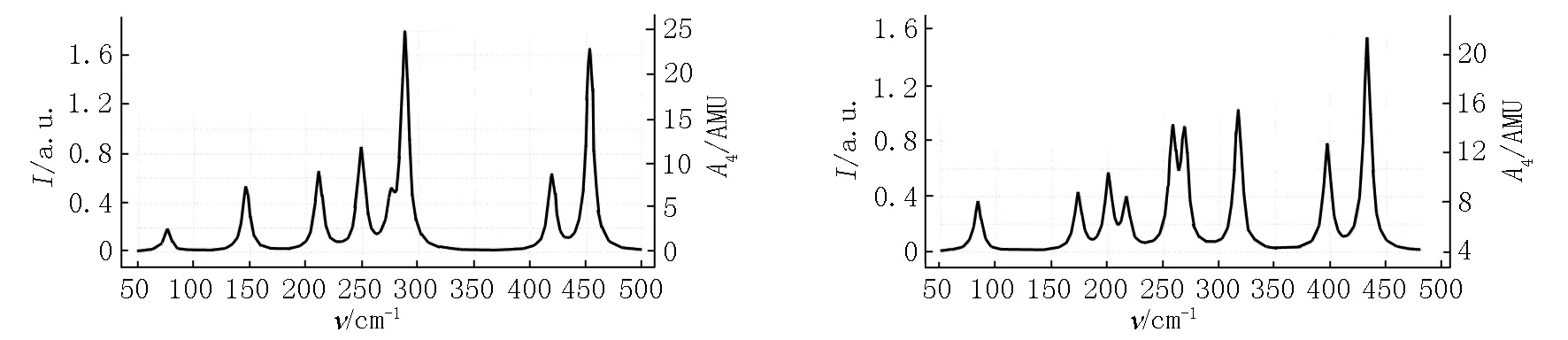
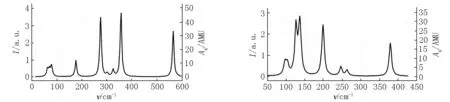
与红外光谱的分析方法相似，由图3可得，构型1(1)有7个振动峰，分布趋势为右侧和中间大、左侧较小，其中最高峰的波数为288.42 cm-1,振动形式为整体变形的弯曲振动，次高峰的波数为453.59 cm-1,振动形式为Co1—Co2—P5和Co2—Fe4—Co3的面内剪式振动；构型2(1)有9个振动峰，分布趋势与构型1(1)相似，其中最高峰的波数为433.15 cm-1,振动形式为P5—Co1—Co3和Fe4—Co1—Co2的面内剪式振动，次高峰的波数为317.39 cm-1,振动形式为整体变形的弯曲振动；构型3(1)有5个振动峰，分布趋势为中间大、右侧小且左侧最小，其中最高峰的波数为357.06 cm-1,振动形式为Co2—Fe4—P5和Co1—P5—Co3的面内剪式振动，次高峰的波数为275.40 cm-1,振动形式为Co1—P5—Co3的面外摇摆振动和Co2—P5—Fe4的面内剪式振动；与单重态其他构型相比，构型3(1)特征峰的分布和几何形态均不相同，这说明构型的几何形态会对其拉曼活性产生影响.构型1(3)有7个振动峰，主要集中分布在两侧，其中最高峰的波数为198.85 cm-1,振动形式为整体变形的弯曲振动，次高峰的波数为126.41 cm-1,振动形式也为整体变形的弯曲振动；相比于单重态构型而言，构型1(3)最高峰和次高峰发生了一定的红移,这说明构型的自旋多重度也会对其拉曼活性产生影响.

结合图2和图3不难发现:与红外光谱图相比，在拉曼光谱图中大部分拉曼活性强的频率区间，其红外活性较低，这验证了红外光谱图与拉曼光谱图的互补性.同时,在单重态构型中其红外活性最强的峰值所对应频率的拉曼活性也较强；而在三重态构型中，其红外活性最强的峰值所对应频率的拉曼活性则较弱.

1(1) 2(1)

3(1) 1(3)

2.3.2 极化率 由于拉曼活性与诱导偶极矩μ(μ=αE，其中α为极化率，E为外加电场强度)有关，因此,当E恒定时，拉曼活性与其极化率密切相关.将计算后所得极化率列于表2中.

由表2可知:所有优化构型极化率张量主要集中在xx、yy和zz主轴上.在单重态构型中，构型1(1)和构型2(1)极化率张量分布相似、大小相近，这表明2者的拉曼活性相近，这验证了在拉曼光谱分析中关于2者拉曼光谱图分布相似的结论.而对于构型3(1)而言，虽然其极化率张量分布及与构型1(1)和构型2(1)较为相似(均由xx、yy和zz主轴提供),但极化率大小和拉曼光谱图均相差较大，这说明极化率张量大小是影响其拉曼活性的关键因素.结合图1可知:在所有单重态构型中，构型3(1)的几何形态与构型1(1)和构型2(1)均不相同，这表明几何形态会对其极化率大小产生影响，进而对其拉曼活性产生影响.在三重态构型中，虽然构型1(3)的极化率张量分布与单重态构型相似(亦均由xx、yy和zz主轴提供),但是其大小相差较大，这说明构型的自旋多重度会对其极化率张量大小产生影响.同时，结合上述关于单、三重态构型的拉曼光谱图论述，不仅可验证“构型的自旋多重度会对其拉曼活性产生影响”的结论，也可进一步得出:构型的自旋多重度通过影响极化率张量大小来对其拉曼活性产生影响.

表2 团簇Co3FeP各优化构型的极化率

3 结论

本文在较高的量化水平下，对团簇Co3FeP进行优化计算,在排除相同构型和虚频后，得到了4个优化构型.通过对其优化构型图、红外光谱和拉曼光谱进行深入研究和预测后，得出如下结论:

1)所有构型均为C1对称,其中构型1(3)的能量最低.

2)对于红外光谱图而言，构型1(1)和构型2(1)的分布趋势均为两侧大、中间小；构型3(1)的分布趋势为右侧大、中间小且左侧最小；构型1(3)的分布趋势为集中在两侧及中间.同时，除构型1(1)有7个特征峰外，其他构型均有6个特征峰，并且构型1(3)的最高峰和次高峰相比于单重态构型而言均发生了一定的蓝移.

3)构型的几何形态和自旋多重度均能通过影响其偶极矩值来对其红外活性产生影响.

4)对于拉曼光谱图而言，构型1(1)和构型2(1)虽然分别有7个和9个特征峰，但是其分布趋势均为左侧较小、右侧和中间大；构型3(1)有5个振动峰，分布趋势为中间大、右侧较小且左侧最小；构型1(3)有5个振动峰，分布趋势为中间大、右侧小且左侧最小，相比于单重态构型而言，其最高峰和次高峰发生了一定的红移.

5)构型的极化率主要由xx、yy和zz主轴提供，其张量大小是影响其拉曼活性的关键因素.同时，构型的几何形态和自旋多重度均能通过影响极化率张量的大小来对其拉曼活性产生影响.