楼梯清洁机器人休息平台路径规划研究

刘井海,张 磊*,李红兵,姚兴田,苏 雷

(1.南通大学机械工程学院,江苏 南通 226019;2.上海交通大学仪器科学与工程系,上海 200240)

0 引言

近年来,国内外不断研发楼梯清洁机器人.2011年,日本研发了一种带撑脚的箱体式楼梯清洁机器人[1];2012年中国设计了一种利用平行四边形的形变特点实现上下楼梯功能的清洁机器人[2];Liu Chaochung等[3]利用8足结构设计了一个能够进行楼梯打扫的清洁机器人.常见的轮式、履带式[4]和升降伸缩式[5]爬楼机器人大多数是为了设计快速通过楼梯或台阶,不太适合于楼梯清洁,仅少数部分可以对楼梯台阶面进行清扫.目前关于楼梯清洁机器人在休息平台的遍历问题和机器人何时下楼、如何下楼的问题的研究较少.

楼梯清洁机器人不仅仅是针对整个楼梯台阶面进行清扫,还应设计合适的路径规划算法以满足楼梯休息平台的清扫,并完成从楼梯到休息平台再到楼梯的过渡, 这些都是在实际使用时需要解决的问题.在到达休息平台后,由于楼梯的特殊环境,所以机器人只有按照有规律的方式进行清扫才能保证机器人的下楼位姿;在机器人遍历整个休息平台后,还需要解决平台区域的判别问题,判断前方是否是往下的楼梯,完成向楼梯的过渡.目前对此类问题的研究较少,采用何种路径规划对休息平台进行遍历、机器人如何“知道”休息平台遍历结束的问题是实现楼梯清洁机器人连续性工作必须要解决的问题.

传统全覆盖路径规划算法的思路是:机器人利用简单的控制算法控制机器人运动方向,当机器人遇到无法前进的区域时,如何控制机器人转向,从而覆盖所有可行区域.这种算法主要分为3类:(i)随机覆盖路径[6](见图1),该方法在控制上相对容易,对机器人的感知能力和规划计算能力要求也不高.但是,随机覆盖方法的执行代价高和效率低,实现全区域的覆盖需要耗费更多的时间、出现较高的重复率[7];(ii)犁田覆盖路径[8],该方法使机器人直线运动,当遇到无法通过区域时则转向朝着相反的方向运动,其路径如图2所示,该方案的可靠性和重复度有了较大的提高,控制过程也相对简单,但是转弯次数较多,会降低其工作效率;(iii)梳状覆盖路径[9]是指机器人从原点开始,沿着分支前进,在遇到障碍物时原路返回,顺着主路径方向平移1个步长,然后继续沿着分支清扫,当机器人来到主径末端时,则逆时针选择另一面墙壁作为参考方向,重复之前的清洁规划,其路径如图3所示,该方案避免了死角区的出现,清扫覆盖率高,而且清扫路径都是相邻的直线,简化了坐标系的计算,但是重复率较高.

这类遍历算法没有解决从平台到下楼的过渡问题,而且,还要求机器人具有良好的定位功能和高端传感器.鉴于上述考虑,本课题组提出了新型的爬楼方式——平动旋转腿式上下楼,并在此基础上研发了一种能够实现上下楼、清扫台阶面和休息平台的清洁机器人[10].

图1 随机遍历示意图

图2 犁田遍历示意图

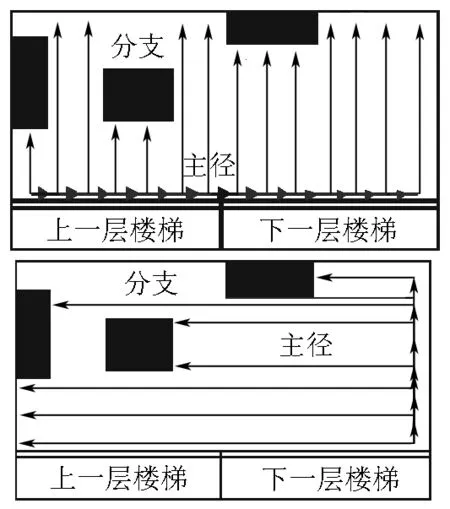
图3 梳状遍历示意图

1 清洁机器人设计

清洁机器人在工作区域的路径规划属于全覆盖式寻优,规划的目标是实现机器人最大覆盖.

路径规划可以提高覆盖率、减少能量消耗、降低遍历时间、缩短路径全长.研究表明:转弯动作是清洁机器人最耗能、耗时的动作,直线运动消耗较少.而且,直线运动的累积误差相对较小.因此,最优的路径规划是最小的转弯次数.然而对于清洁机器人的有些结构,转弯和直线运动的能量消耗差别不大,有些定位方式弧运动累积误差相对较小.因此,全覆盖的方法与机械结构设计相关[11-12].

1.1 清洁机器人结构

如图4所示,清洁机器人由1个旋臂电机、2个步进电机、2个驱动轮、1个万向轮和1个探空轮组成.旋臂电机带动机器人两侧旋臂旋转完成机器人上下楼动作.步进电机通过改变输入的脉冲频率可使2个驱动轮获得不同的速度,从而实现清洁机器人前进、后退和转弯等功能.

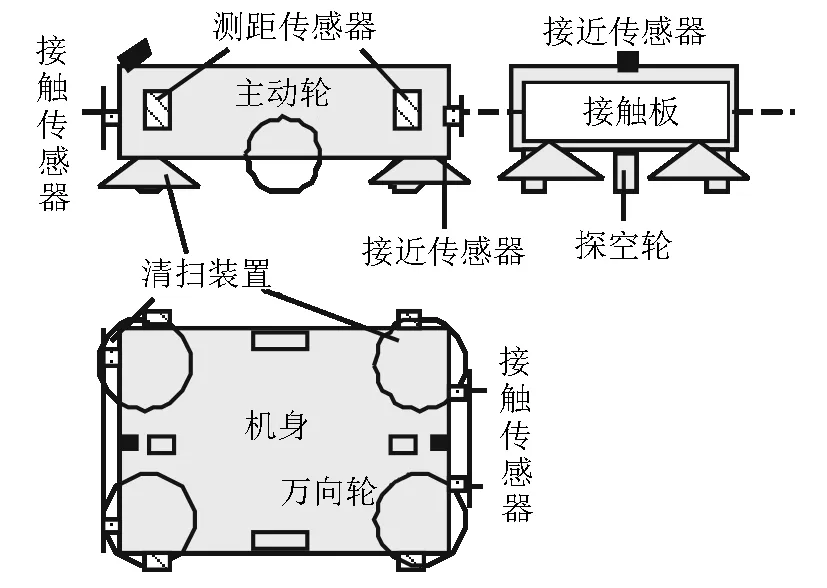
(a)机器人3视图

(b)机器人传感器布局

1.2 清洁机器人传感器布局

为了能够适应复杂的情况和环境并能进行自主地运动,机器人需要通过传感器获取外部环境信息,感知环境变化,控制机器人做出相应的动作.

由于每个传感器模块都有自身的缺陷,因此,需要运用多传感器信息融合技术,把多个传感器按照一定的准则进行组合,从而获得对被测对象的一致性解释或描述,解决单传感器由于自身精度、分辨率和环境因素造成的输出数据缺陷,提高环境系统的可靠性和鲁棒性[13-14].

如图4(b)所示,红外接近传感器通过利用被检测物体对光束的遮挡或反射来检测前方是否是向下的楼梯,接触式传感器用于检测机器人前进方向是否有障碍物.机器人左右两侧各安装有2组测距传感器,检测机器人与其他移动物体或墙壁之间的距离,从而保证机器人与障碍物的安全距离.为了避免踏空,传统机器人采用向下探测的光电传感器,但清洁机器人下方扫刷扬起的灰尘会导致传感器误判,考虑到楼梯清洁机器人需要频繁地判断是否踏空,提出使用接触式传感器,设计了一个侧轮可以上下微动的探空轮,检测前方是否踏空.

1.3 清洁机器人运动模型

清洁机器人运动模型[15-16]如图5所示,其中X、Y为绝对坐标,XR、YR为相对坐标.机器人左轮线速度为VL,右轮线速度为VR,质心的速度为VC,机器人的位姿向量P=(xC,yC,θ)T,因此VL、VR、VC之间的关系为

VC=(VL+VR)/2.

图5 全局参考坐标系和局部参考坐标系

根据刚性平动原理,机器人的平动和旋转都可以看作是绕机身瞬心C的转动,其旋转半径为

R=VC/ω=D(VL+VR)/(2(VL-VR)).

机器人有3种运动模式:(i)VL=VR,机器人直线运动;(ii)VL=-VR,机器人原地旋转;(iii)VL≠VR,VC=(VL+VR)/2,机器人圆弧运动.根据刚体力学知识可知,

2 楼梯休息平台路径规划研究

犁田覆盖可使机器人以最短路线覆盖休息平台,在保证休息平台覆盖率的同时,也方便机器人寻找向下的楼梯.确定犁田覆盖路径首先需要明确犁田覆盖的主路径选择.但是,犁田覆盖路径的终点位置会依据犁田覆盖的主路径方向和休息平台的宽度而发生变化.

如图6所示,休息平台左下段是上级台阶踢面,而右下段是下一层楼梯的探空区域.若清洁机器人以休息平台长边作为主路径进行覆盖遍历,则由于平台或者机器人本身尺寸问题,所以在清洁过程中可能会出现 “边缘效应”,即机器人在结束覆盖的那一条矩形边缘地带上会留下宽度小于机器人本体宽度的一条未覆盖地带.若当机器人检测到车身一侧与对面墙壁之间的距离小于一个车身时,机器人接近对面墙壁,则机器人的结束位置为休息平台的左上角A或右上角B.但这2个位置无法保证靠墙一侧是否清扫,且不能作为休息平台的最终结束位置.当机器人选择休息平台短边作为主路径遍历时,机器人的探空轮会对下一层楼梯位置进行探空,通过探空次数来判断休息平台是否完全遍历.此时机器人可以以探空次数为终止条件,其结束位置是C,机器人正对着下一层楼梯边缘,机器人可执行下楼动作,然后重复进行楼梯清扫工作.

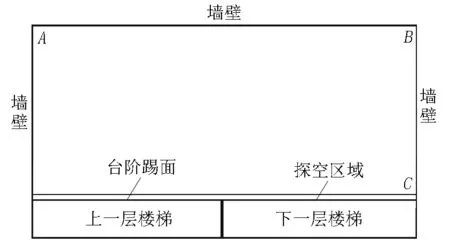
图6 休息平台示意图

机器人的全覆盖方法与机器人的结构形状有关.已研究的覆盖路径算法大多数是圆形壳体,而楼梯清洁机器人的车身为了完成楼梯台阶面的清扫工作采用的是长方形车体.长方形车体在墙壁或障碍物转身时比圆形会遇到一些问题,当机器人作原地自旋90°运动时,长方形车体会出现车身被卡住的情况(见图7).

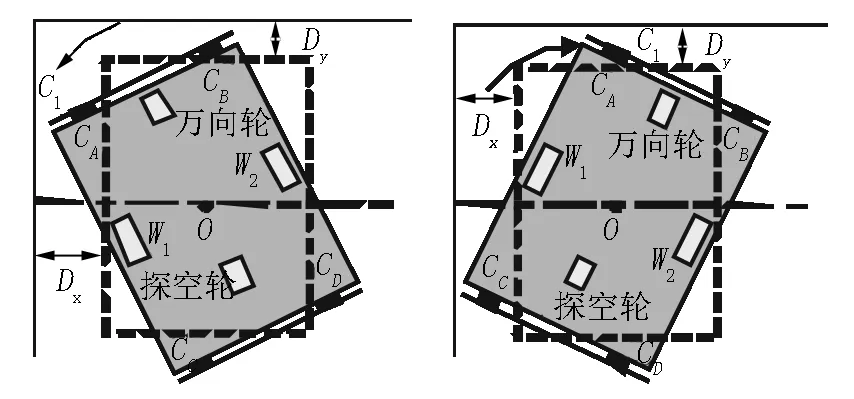
图7 机器人原地转身被卡住示意图

当机器人左上角C1与墙壁发生磕碰时,长方形车体会导致机器人被卡住而不能旋转90°,虚线框表示机器人前一动作的姿态.为使机器人能够完成转身,需要通过调整机器人与障碍物的安全距离(见图8).

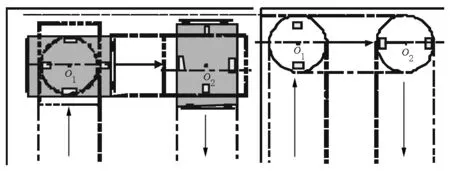
图8 机器人犁田覆盖路径示意图

机器人沿着虚线行走,当检测到前端存在障碍物时,相比于圆形壳体,长方形的壳体为了避免转身被卡住需要留出更多的安全距离.

该方法解决了楼梯机器人的自旋运动,但会降低清扫覆盖率.图9(a)、图9(b)分别是犁田覆盖和梳状覆盖清扫边界示意图.

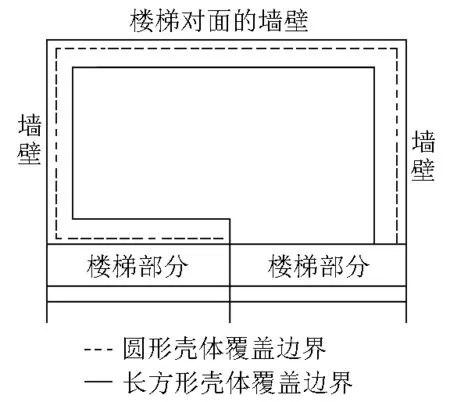
(a)犁田覆盖边界

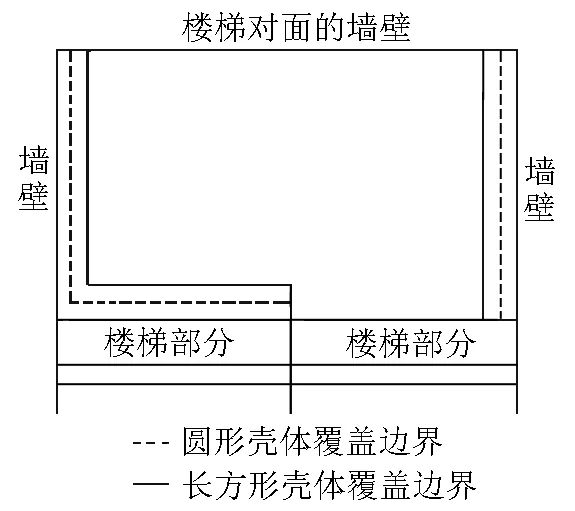
(b)梳状覆盖边界

2.1 基于犁田覆盖的改进路径规划

为了解决楼梯清洁机器人在休息平台上的过渡问题,结合随机覆盖、犁田覆盖与梳状覆盖的优点,本文提出了一种基于犁田式算法的改进路径规划,步骤如下:

(i)当机器人到达休息平台后,环境信息由沿边走算法[17]确定.首先,清洁机器人沿着墙壁或靠墙障碍物行走一周,通过两侧的测距传感器、前后端的碰撞传感器以及探空轮获取平台信息(见图10).在机器人沿边学习的同时,控制系统采集运动系统左右驱动轮编码器的脉冲频率信号,待行走结束之后可以大致描述出环境轮廓.

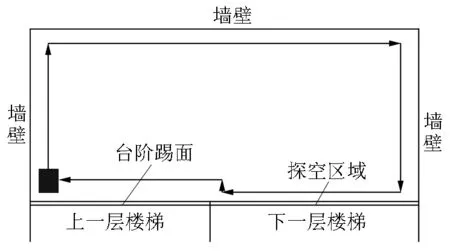
图10 机器人沿边走路径图

(ii)当确定遍历区域之后,机器人根据确定的主路径方向开始遍历(见图11(a)和图11(b)).当机器人前端检测到墙壁或障碍物时,减速前进,并在设定距离处停车.以机器人的中心O为旋转中心逆时针旋转一个角度θ,反向行走;当到达图11(c)所示的位置时,机器人底部碰撞传感器收到信号,机器人再顺时针旋转θ角进行往返式行走.其运动全图如图11(e)所示.

(a)机器人遇障 (b)机器人转身

(c)机器人反向转身 (d)再次遇障

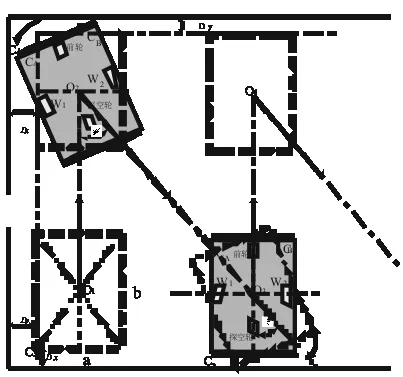
(e)运动全图

(iii)机器人两侧各有2个超声波测距传感器组,用于贴墙障碍物.机器人在直线行走时会根据同侧传感器的返回值判断其左侧是否有凹处(见图12).当机器人直线行走到图12中①位置时,其前后2个传感器返回的信号不同,判断左侧是凹处;机器人在从①位置到②位置的过程中需要对距离进行信息采集,根据这个距离计算往返次数,然后不断转弯或直行来回清扫.

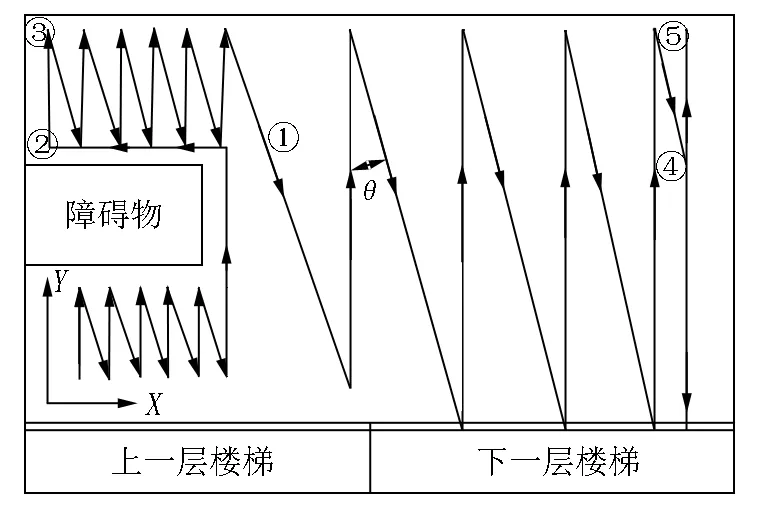
图12 改进路径示意图

(iv)当清洁机器人遇到孤立障碍物时,其运动规律与贴墙障碍相似.对于非直线型障碍物,机器人将会采用折线逼近算法[18](见图13).为使机器人在避障之后回到原来的路线,将其行走路线简化为符合纯平动和纯转动的情况,则机器人行走避障路线应满足如下条件:

(4)

其中θi为第i段路径与第i-1段路径之间的夹角,Li为第i段路径的长度.

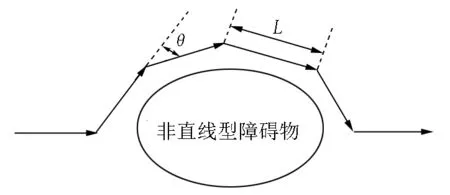
图13 折线逼近行走路径

相比于遗失覆盖算法[19],采用折线逼近算法能减少清扫盲区,实现更高的覆盖率.

(v)当清洁机器人遇到死角区位置(即机器人的前方和右侧都有障碍物,后方和左侧是已经遍历清扫过的区域)时,机器人反向运动逃离死角区[20].

楼梯清洁机器人在整个覆盖过程中工作时间可以用如下公式来描述:

T=T1+T2,

其中T为工作时间,T1为直线运动时间,T2为转弯运动时间.机器人工作行进速度为v,有效覆盖宽度为b,在直线运动中速度v近似为一个恒定值,则直线行走时间为T1=s/v;楼梯清洁机器人在每次转弯时的轨迹基本相同,因此转弯时间为T2=NT0,T0=θπ/(180°ω),其中T0为每次转弯时间.

2.2 几种路径算法比较分析

楼梯清洁机器人参数:机器人长度a=400 mm;机器人宽度b=250 mm;清洁速度v1=200 mm·s-1;转弯速度v2=40 mm·s-1.

由图14(a)可知:在机器人90°转身时,其顶角位置C轨迹都是以O为圆心、R为半径的圆弧.故机器人中心距离墙壁距离相同,即Dx+b/2+γ=Dy+a/2+γ,其中γ是裕量.由图14(b)可知:X1=125 mm,X2=Rcos(58°-θ) mm.由几何关系可知X2-X1≥Y2-Y1,且θ的值不宜过大,故改进算法安全距离取大值Dx=Dy=X2-X1≤40 mm.

图15(a)是犁田算法无法覆盖区域的2维图,从该图可以得到未覆盖区域面积:

S1=2WDx-3(L/2-Dx)Dy,

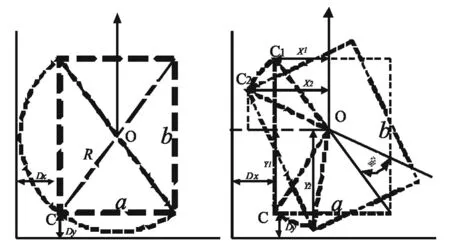
(a)90°转身示意图 (b)小角度旋转示意图

同理可以从图15(b)得到梳状覆盖未覆盖区域面积S2=2WDx+(L/2-Dx)Dy,改进路径未覆盖区域面积S3=2WDx+3(L/2-Dx)Dx.运用数学关系进行简化运算得Dx=Dy+C,其中C=(a-b)/2,则

S1=-3Dx(Dx-2/(3W)-L/2-C)-3LC/2,

S2=-Dx(Dx-2W-L/2-C)-LC/2,

S3=-3Dx(Dx-2/(3W)-L/2).

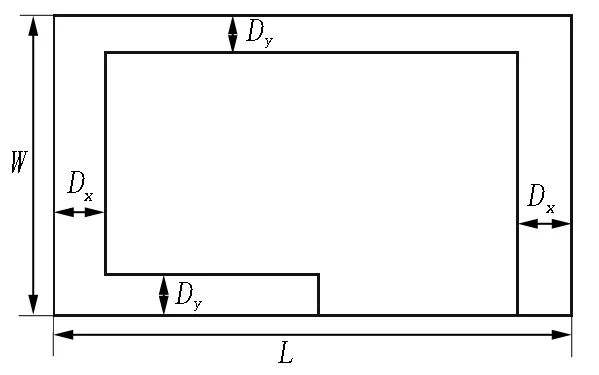
(a)犁田覆盖几何图

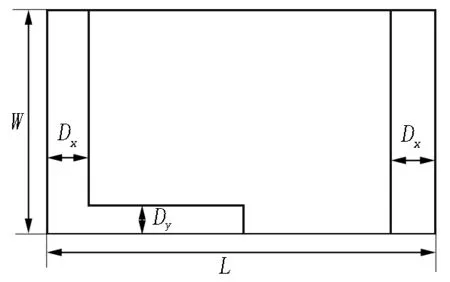
(b)梳状覆盖几何图

根据楼梯设计规范可知L≈2W,又由Dx≪W和2次函数图像可知,随着Dx的增大,未覆盖区域面积以2次方形式增大,降低覆盖面积.

由表1可知:改进路径覆盖的直线运动距离大于犁田覆盖的.但是可以达到更好的清扫覆盖率,也可以极大地降低转弯时间,减少机器耗能.当楼梯休息平台的面积较大时,这种优势更加明显.

表1 算法比较分析

3 实验仿真分析

改进的路径规划依然满足犁田路径的覆盖率模型,清扫覆盖面积随着时间的增加而逐渐增大.但旋转角度θ的变化会直接影响机器人每次的横向偏移距离x=ytanθ,从而影响机器人在休息平台上的整体覆盖率和工作时间.因此,针对角度θ的变化需要进行仿真实验来验证路径的规划性和可靠性.

3.1 仿真分析

为了保证休息平台的覆盖率,机器人每次偏转的横向距离应该满足x≤b,设θ0=arctan(b/W),θ0为机器人临界旋转角.

在VC++6.0环境下进行了仿真实验:设置休息平台面积为1 984 mm×1 128 mm.如图16所示,仿真界面的边界模拟休息平台的墙壁,中间空白区域表示待覆盖区域,右下角区域表示下楼位置(即探空区域),黑色表示机器人的已覆盖区域,白色线条表示机器人路径轨迹.

针对不同旋转角θ进行仿真实验,图16分别为仿真平台环境、7°实验、8°实验和9°实验路径图.由图16(b)可知机器人转弯横向偏转距离小于机器人车身宽度,即2次分支之间有一定重合度.图16(c)和图16(d)的机器人偏转距离均略大,转弯次数和行走路径都有所降低,但是机器人的覆盖率也均有所降低.

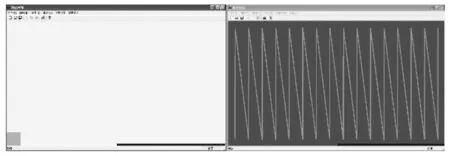
(a)仿真环境 (b)7°实验

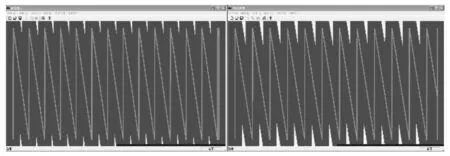
(c)8°实验 (d)9°实验

以机器人路径长度作为覆盖参数,经过多次实验发现改进后的路径规划满足正比例模型分布,其覆盖率与机器人路径长度关系如图17所示.

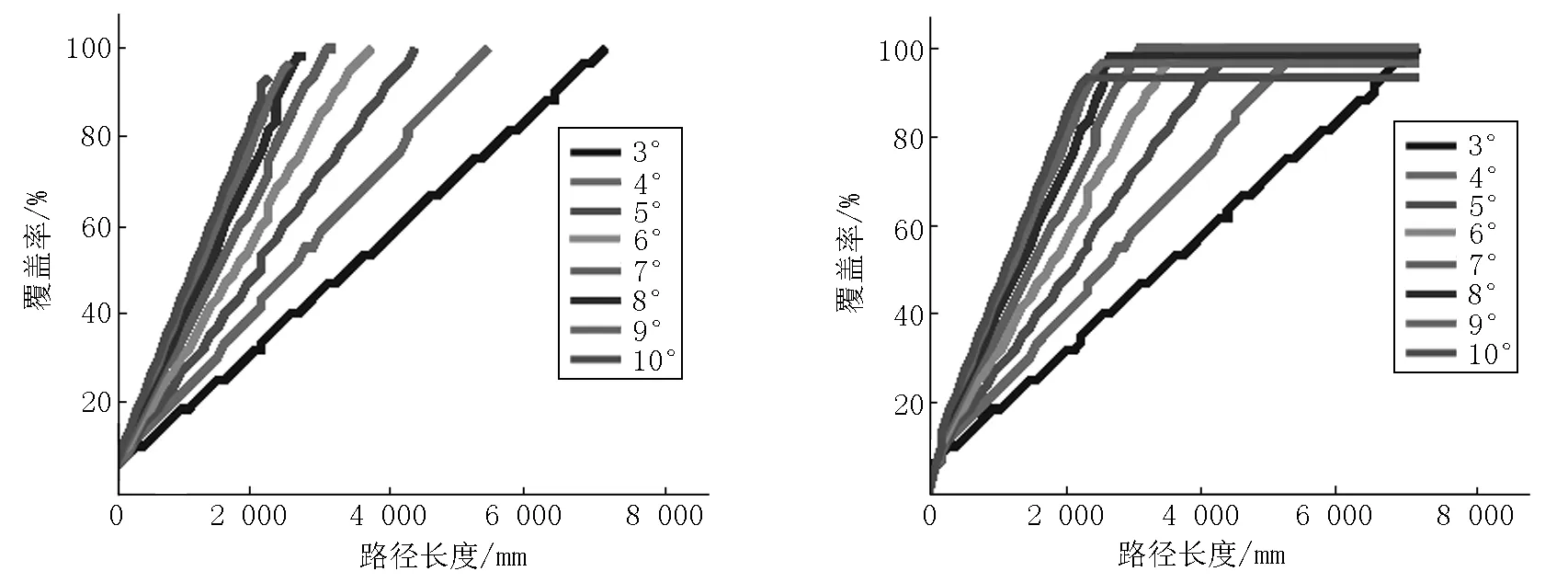
(a)路径与覆盖率 (b)最终覆盖率

由图18(a)可知:随着θ的增大,机器人以较少的转弯次数就能够较好地完成覆盖任务.

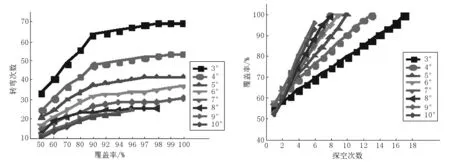
(a)转弯次数 (b)探空次数

楼梯清洁机器人的连续性工作不同于平地机器人,机器人需要知道何时完成休息平台的遍历.研究发现:随着探空次数的增加,机器人的覆盖率也在增加.当探空次数达到一定值时,可以认为休息平台已经完全遍历,仿真结果如图18(b)所示.

综上所述,发现当偏转角度θ<θ0时,机器人的重复率较高,降低了机器人工作效率;当θ>θ0时,机器人的覆盖效率提升效果显著,但是也会降低机器人的覆盖率;当θ≈θ0时,机器人的工作效率有着显著提高,也能满足覆盖率的要求.因此,机器人在直线前进过程中,需要计算出位置坐标O(x,y),并存储一系列数据:Xmin、Ymin、Xmax、Ymax,由此得到W=Ymax-Ymin,进而可以确定合适的旋转角.由于休息平台的特殊性,所以其X方向只有1/2的长度满足机器人的探空条件:当探空次数C=L/(2b)+1时,可以认为休息平台已经全覆盖,机器人可以下楼.

设置实验环境对犁田覆盖、梳状覆盖和改进路径覆盖进行无障碍路径仿真.计算结果如表2所示.

表2 几种路径规划对比分析

由表2可知:改进路径相对于另外2种覆盖算法留出的安全距离较少,保证了机器人的覆盖率,同时改进路径的机器人转弯角度远远小于90°,减少了清扫总时间.由此可知改进的路径虽然重复率高于犁田覆盖,但总体而言,其在覆盖效率和遍历时间方面的实用价值高于另外2种覆盖.

3.2 实验验证

为了验证文中改进路径的有效性,以现有的楼梯清洁机器人进行相应的实验.实验环境大小为4 000 mm×1 980 mm,图19和图20分别为无障碍和静态障碍物实验,对机器人路径、时间和探空次数进行实验.

图19 测试实验区域环境图

图20 清洁机器人探空次数与覆盖率实验

在实际行走过程中,由于转弯精度和系统误差,所以楼梯清扫会出现一些遗漏和重复.经过多次反复试验,楼梯清洁机器人的覆盖率达到95%以上.同时验证了机器人前方探空轮的有效性,一旦踏空,机器人会立即撤回,防止跌落.通过记录探空次数来判断机器人在休息平台上的遍历程度是可行的.

分析实验误差原因:(i)机器人定位与实际略有偏差.机器人轮胎在光滑地板上行走可能会导致滑轮,使得传感器测量的行走距离大于实际距离.机器人转弯角度存在偏差,累积的偏差导致较大的误差.(ii)机器人的转向精度不是很高.其原因可能是机器人左右电机的差异.

4 结论

本文提出了一种基于犁田算法的改进“N”形路径规划用于解决楼梯清洁机器人休息平台过渡的问题.通过改变机器人旋转角度有效地提高了覆盖率和工作效率;通过对机器人休息平台覆盖率与探空次数建立数学模型,实现了机器人从休息平台到向下楼梯过渡的问题.仿真结果表明:该方案的多个性能指标都得到了提高,不仅保证了遍历所有可到达的工作区域,而且大大降低了机器人的总体耗时和能耗.只需要若干传感器以及记录探空次数就能保证清洁机器人楼层清扫的连续性,这显示了该方法的优越性和有效性.