一类Kirchhoff方程正规化解的存在性和唯一性
2022-05-27 09:00王诗颖
湖北文理学院学报 2022年5期
丁 凌,王诗颖
(1.湖北文理学院 数学与统计学院,湖北 襄阳 441053;2.三峡大学 理学院,湖北 宜昌 443002)
其中x∈RN(N=1,2,3),a,b>0,r∈(0,2)和p∈(2,2*)。在正规化条件下和不同范围p下,用分析的方法,得到了此方程正规化解存在性和唯一性结果。这一结果推广了r=1特殊情形下相关文献的结论。
1 引言
本文研究一类Kirchhoff方程:
(1)
其中x∈RN(N=1,2,3),a,b>0,r∈(0,2)和p∈(2,2*)。这里如果N=1,2时,2*=+∞;如果N=3时,2*=6。当r=1时,方程(1)就变成了

(2)
这类问题起源于方程
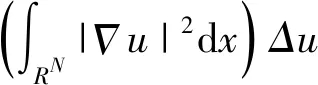
先在空间H1(RN)定义等价范数:
另外用记号‖·‖q表示Lq范数。回忆一下著名的带有最优函数Q(x)的Gagliardo-Nirenberg不等式[8]:
(3)
且当u=Q时等号成立。其中Q是如下方程唯一的基态解(平移意义下):
于是,由Q满足的Pohozaev等式和Nehari等式可得:
(4)
类似于文献[8],可证式(3)所有的最优函数都是经过Q(x)平移和伸缩的,属于集合
{αQ(βx+y)∶α,β∈R+,y∈RN}
(5)
受文献[5]的启发,考虑如下极小问题:
(6)
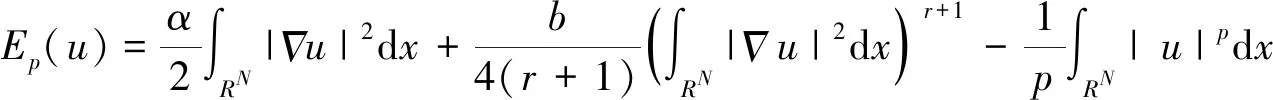
(7)
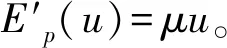
(8)
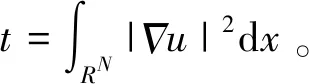
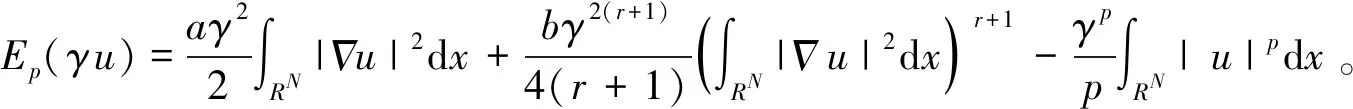
对任意的c>0和p∈(2,2*),都有Ip(c)≤0成立。
(9)
2 主要定理及证明
本文主要定理如下:
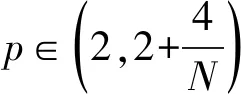
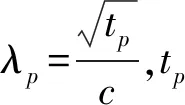
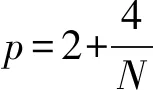
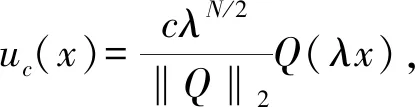
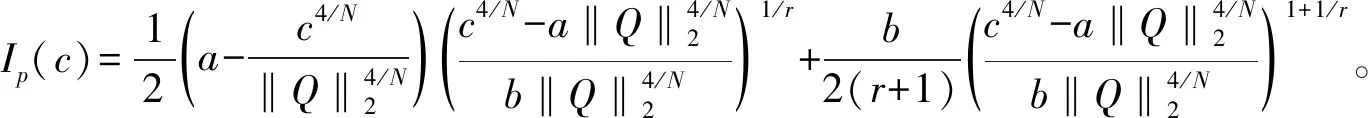
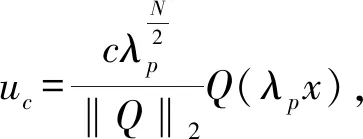

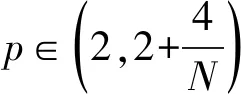
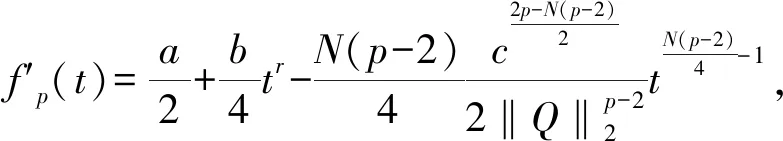
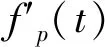
(10)
另一方面,设
(11)
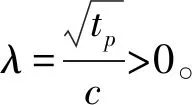
代入式(7)得
(12)
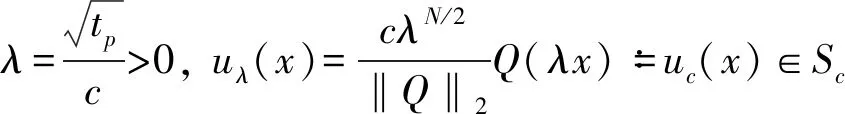
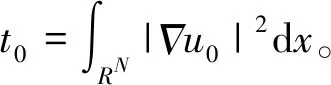
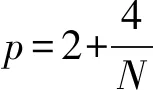
(13)
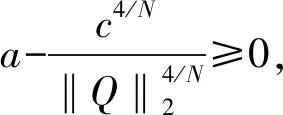
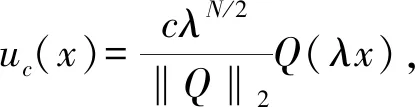
从而也是方程(1)的正规化解。由式(6)(8)和(13)可得
唯一性用(i)中同样的方法可得,在这里省略证明。

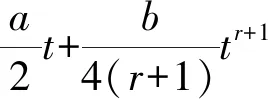
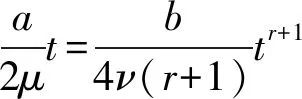
(14)
再结合式(8)和(14),可得
(15)
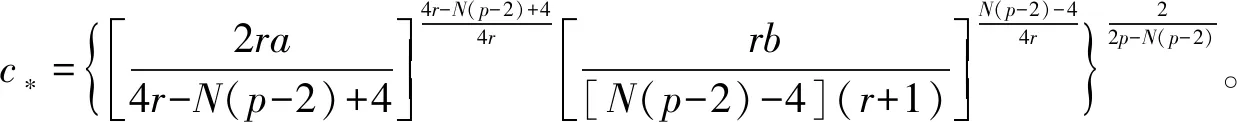
唯一性用(i)中同样的方法可得,在这里省略证明。
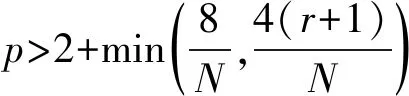
猜你喜欢
波谱学杂志(2022年1期)2022-03-15
数学小灵通(1-2年级)(2020年9期)2020-10-27
安阳工学院学报(2020年4期)2020-09-11
汉字汉语研究(2020年1期)2020-04-21
新高考·高一数学(2018年5期)2018-11-22
中国校外教育(下旬)(2017年8期)2017-10-30
诗选刊(2015年6期)2015-10-26
考试周刊(2015年105期)2015-09-10
诗歌月刊(2009年4期)2009-05-22
杂文选刊(2008年2期)2008-05-14

