随机需求下仓储网络能力分配模型研究
王承娜,徐光明,秦 进
(1.福州外语外贸学院 经管学院,福建 福州 350202;2.中南大学 交通运输工程学院,湖南 长沙 410075)
随着移动技术的发展,线上购物规模持续增长,推动电商行业高速发展。资料[1]显示,2020年中国电商行业市场规模已达到27.5万亿元,规模越大,竞争越激烈。在这竞争日趋激烈的市场中,为了更好更快地满足消费者,电商企业需要将商品靠近消费者区域储存,于是产生分仓存储商品需求。因此,第三方仓储企业传统的单仓服务很难满足电商企业需求,迫切需要在更大范围布局仓储网络提供分仓服务。但电子商务具有商品需求不确定性和分散性的特点,该如何有效分配仓储能力,更好为电商企业提供分仓服务,提高收益,成为第三方仓储企业亟待解决的问题。
过去对仓储系统的研究主要集中于单仓仓储规划与布局[2-3]、仓储运作[4-5]、仓储拣选路径[6-7]以及仓储库存策略[8]。大多数关于仓储系统的分析主要关注成本控制[9],较少关注利润最大化。近几年,鉴于仓储业务外包的迅猛发展,第三方仓储的收益管理问题正不断引起理论者和实践者的关注:Lin[10]提出一个随机动态规划模型对第三方仓储的分配策略进行分析;Xu[11]基于收益管理的思想,应用鲁棒优化求解对随机市场需求条件下的第三方仓储能力配置问题进行研究,但主要针对传统单个仓库能力设计及资源分配建立数学模型。随着顺丰、邮政等诸多企业布局仓储网络(云仓),逐渐有学者开始探讨云仓模式[12-13],但以定性分析为主,相关研究成果还比较欠缺。因此,本文应用收益管理理论,考虑商品储存需求的不确定性,通过建立仓储网络分仓储存能力分配模型,为第三方仓储企业管理者提供决策建议。
1 模型建立
1.1 问题描述
在及时交付的电商模式下,消费者分散分布的特点使得电商企业不得不在各区域储存货物以实现就近发货、快速送达。但自建仓库的高成本往往导致电商企业寻求第三方仓储资源解决分散化储存货物的需求,这促使第三方仓储企业呈现网络化发展布局。第三方仓储企业是为电商企业提供仓储服务的分包商,主要通过租赁仓储空间收取费用。一般情况,第三方仓储企业的仓库网络布局如图1所示,仓储网络由CDC-RDC-DC多级仓库构成。其中,CDC代表中央储存仓库,RDC代表区域储存仓库,DC代表仓储配送仓库,S代表电商企业供应商。在仓储网络中,电商企业只需让供应商将货物集中存放在CDC,进而通过第三方仓储企业的统一调拨、运输,实现货物提前调配至离消费者最近的仓库储存。
对于已建构完成的仓储网络,第三方仓储企业决策者考虑如何最大限度地提高仓储资源利用率,以获得最大收益。鉴于此,本文将仓储网络结构能力分配问题拆分两阶段考虑:1)一个固定储存能力的CDC该如何为N个客户分配资源,即单仓仓储能力分配问题;2)一个由R个DC构成具有固定储存能力的仓储网络,如何将有限的各仓储存能力分配给有分仓需求的客户,即多仓仓储能力分配问题。

1.2 单仓仓储能力分配模型
考虑一个固定储存能力的第三方综合仓库,设计为N种不同品类客户提供仓储服务,各品类货物储存具有一定的差异性,仓储服务价格与成本不同,因此各品类客户带来的收益不一样。由于各品类货物的储存需求不确定,企业需要考虑如何将有限的储存能力分配给各品类客户,使其收益最大化。
假设该第三方仓储仓库以托盘为储存单元,各品类货物占用相同单位托盘空间,不存在托盘混装及分割。相关变量与参数表示如下:Pn为第n类货物单位仓储服务费用,xn为第n类货物分配的仓储能力,Q为单个综合仓库储存能力,Dn为第n类货物仓储需求,Cn为n类货物提供储存服务所需承担的单位成本(储存货物的运营成本、管理成本等),Sn为拒绝n类货物的单位机会成本,πn为第n类货物的收益函数。
针对单仓仓储能力分配问题,应用收益管理理论[10-11,14],考虑仓储能力约束,构建如下报童模型:
(1)
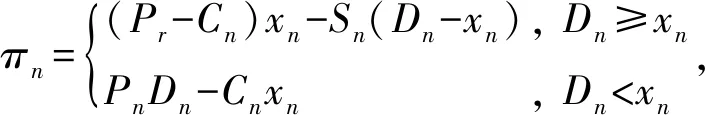
各品类仓储客户的实际需求往往是波动的,具有随机性。假设需求服从概率分布函数F(Dn),即Dn~F(Dn),f(Dn)为其概率密度函数,用E(πn)表示收益期望值,此时模型改写成以收益期望值最大为目标函数:
(2)
1.3 多仓仓储能力分配模型
多仓仓储能力分配需要考虑多个仓库空间利用问题,比单仓仓储能力分配更为复杂。现考虑一个由R个区域仓库构成具有固定储存能力的第三方综合仓储网络。由于货物在各区域储存需求不确定,企业需要考虑如何将有限的各仓储存能力分配给有分仓需求的客户,满足其就近储存需求,同时收益最大化。为便于建立模型,进一步作出假设:1)货物从总仓到每个分仓调拨费用已知,与距离有关;2)电商客户分仓储存需求是随机的,但通过历史数据可以得到需求的分布特征;3)该第三方仓储网络以托盘为储存单元,货物占用相同单位托盘空间,不存在托盘混装与分割。
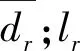
根据问题描述,以第三方仓储企业收益最大化为目标,建立随机需求下的分仓储存能力分配问题模型:
maxE[Prmin{xr,dr}]
(3)
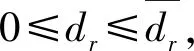
(7)
约束条件(4)表示仓储网络总能力约束;约束条件(5)是对分仓能力的分配应满足各分仓能力上界及满足客户基本需求的下界约束,避免单方面追求收益最大化而导致某些区域分仓没有分配货物的情况出现。约束条件(6)为决策变量的整数约束。
2 模型求解
2.1 单仓仓储能力分配模型求解
现有较多文献[11,15]对单仓仓储能力分配模型的求解作了深入分析,本文简单给出模型(2)的求解思路。
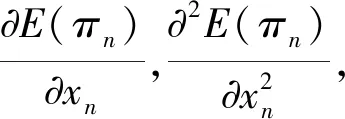
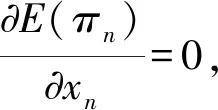

整理得到最优解:
2.2 多仓仓储能力分配模型求解
上述多仓仓储能力分配模型目标函数(7)为非线性函数,约束条件为线性函数,本文通过把模型线性化改造进行近似求解。
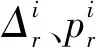
(8)
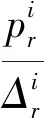
(9)

有如下转化关系:

代入式(9),整理可得:
(10)

(11)
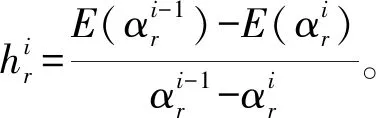

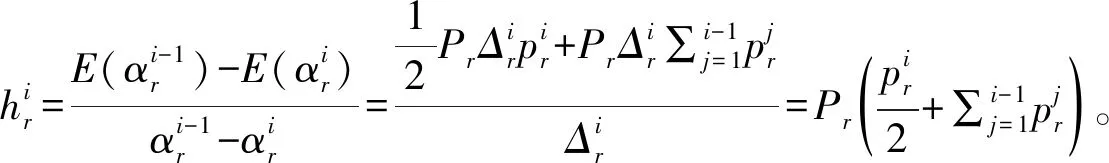
(L1)
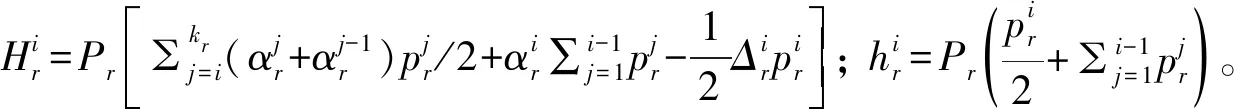

(L2)
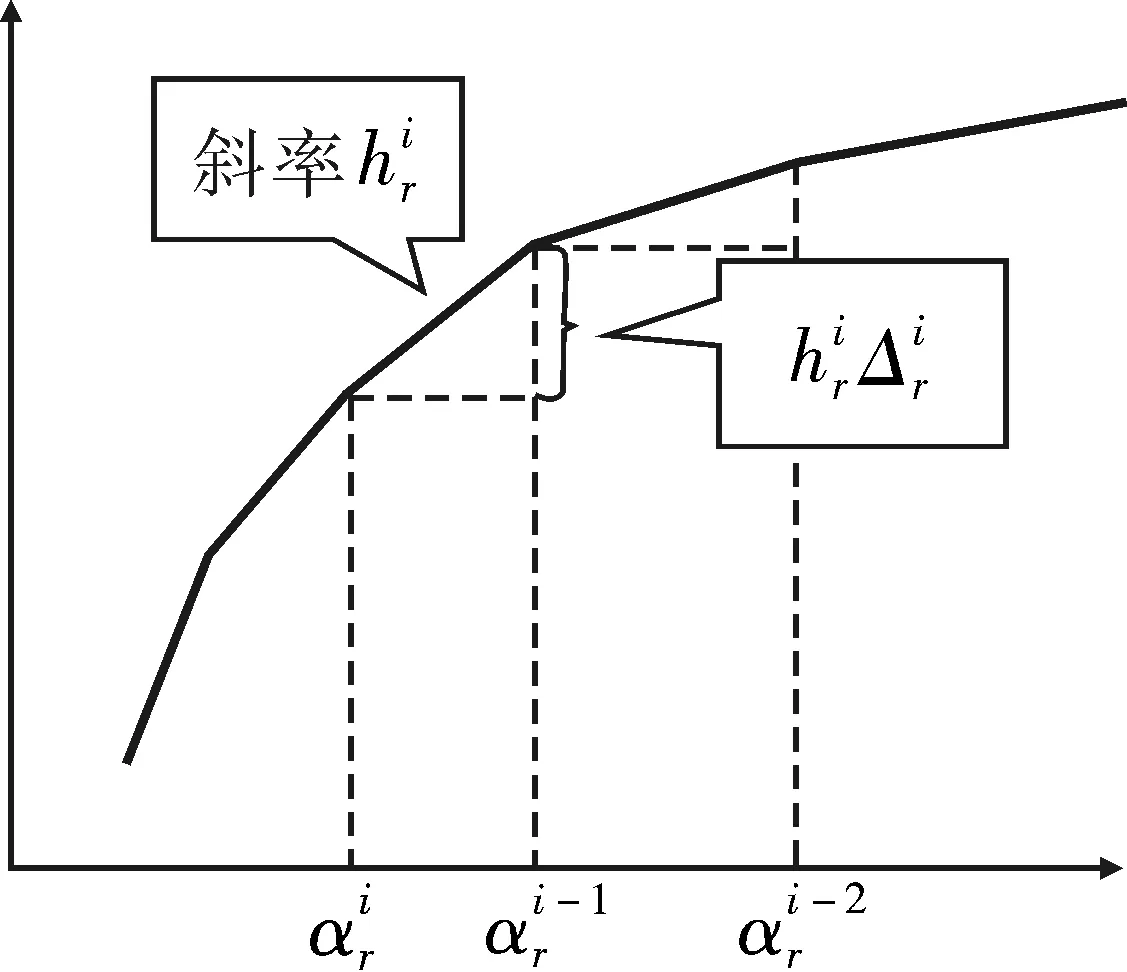
图3 线性化后各分仓客户需求分布函数
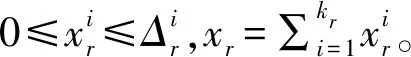

3 算例分析
单仓、多仓仓储能力分配模型为独立的两阶段分布式求解,在单仓仓储能力分配模型求解后给出了各品类货物的储存能力分配值后,可作为多仓仓储能力分配模型中的待进一步分仓的系统能力。
本节主要验证多仓仓储能力分配模型的有效性,假设某第三方物流企业的仓网系统拥有处理一定托盘数量的货物能力,由在不同区域的5个分仓构成,各分仓的信息如表1所示。假设电商客户的各分仓需求服从指数分布函数,见式(12),独立同分布,需求上限值均为500个托盘储存空间。
(12)

表1 各区域分仓信息表
将上述参数代入(L3)求解,考虑最大仓储能力M及K取值变化对结果的影响,计算结果如表2、3所示:
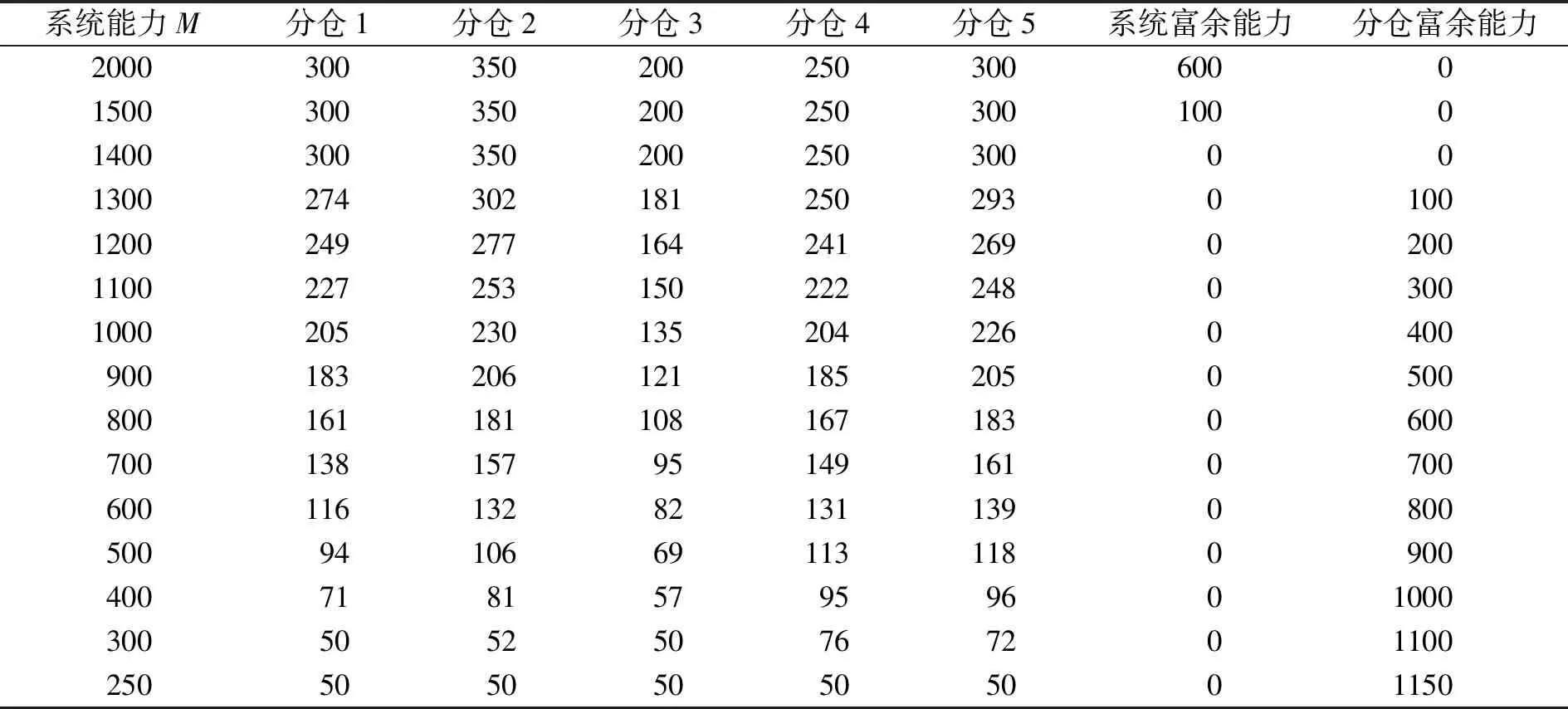
表2 最大仓储能力变化下最优仓储能力分配方案(K=500)

表3 K变化下最优仓储能力分配方案(M=1000)
可以看出:1)各分仓能力分配值随仓储网络最大能力增加而增大。当仓网能力小于分仓总容量时,即M≤1400,各分仓会有富余能力;当大于分仓总容量时,分仓能力分配值受到自身容量约束。
2)在仓网能力较大时,即大于客户总平均需求(M≥900),意味着仓网系统能够满足客户分仓需求。这时,分仓能力分配值取决于客户在各区域的需求分布。如客户对分仓2的平均储存需求最大,则分仓2的能力分配值也最大。而当仓网系统无法满足客户分仓需求时,分仓的能力分配值主要由调拨服务费用起决定作用。
3)对于线性化改造后的多仓仓储能力分配模型求解,需求分布划分的子区间数越大,越能够得到接近于精确解的最优解。从表3的数据可以看出,在100以上数量级的分仓最优解相差不大,说明取K=500下的分仓方案能够较高程度拟合实际情况。
4 结语
本文主要在一般化仓储网络结构的基础上,研究随机需求下第三方仓储网络能力分配策略,提出分阶段优化仓网系统能力模型,通过建立单仓与多次仓储能力分配数学模型,并给出模型求解方法,有效解决电商企业分仓需求与仓储系统资源利用率问题。算例仿真结果表明,在仓网系统能力足够大时,仓储企业能够较好满足电商企业分仓需求,分仓资源分配主要受到电商企业需求分布的影响;而在仓网系统能力不足时,分仓资源分配主要被收取的分仓服务费用影响。第三方仓储企业管理者可以通过有效的运营管理,如区分有无分仓需求的客户,合理规划有限资源的分配,提高仓储系统空间利用率等手段来提高企业收益。

