从动态电路探讨电学元件U-I曲线两种斜率的使用
赵文浩 张佳子 杨荣富
(宁强县天津高级中学 陕西 汉中 724400)
1 提出问题
应用函数图像求解物理问题是高考对“应用数学知识求解物理问题能力”考查的基本形式之一[1].高考试题中利用电学元件U-I曲线斜率求解电阻便是这种背景下常见的一类题型,它也是日常教学过程中一个比较具有争议的难点问题,因此,对于这个问题的讨论具有十分重要的价值.
【典例1】如图1所示电路中,电源的电动势为E,内阻为r,R1为滑动变阻器,R2为定值电阻,电流表和电压表均为理想电表,闭合开关S,当滑动变阻器R1的滑动触头P向右滑动时,电表的示数都发生变化,电流表示数变化量的大小为ΔI、电压表,和示数变化量的大小分别为ΔU,ΔU1和ΔU2,下列说法正确的是( )
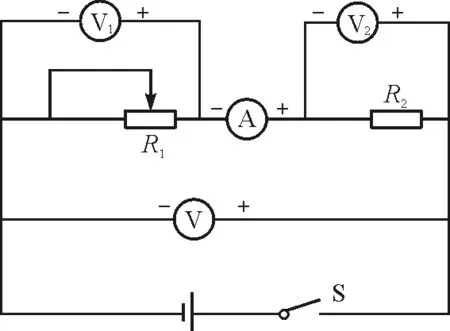
图1 典例1动态电路图

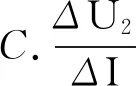
本题说法正确的是选项C.其理由是根据闭合电路欧姆定律得
U1=E-I(R2+r)
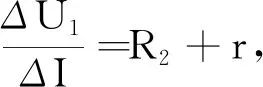
问题1:电学元件U-I曲线的两种斜率分别表示什么物理含义?
问题2:线性元件和非线性元件的电阻分别具有什么性质?
问题3:在动态电路中如何对线性元件和非线性元件的电阻实现求解?
在习题处理时,若是直接根据答案上的方法求解,虽然能够对本题做出正确选择,但是学生却无法理解这样求解的原因,增加了问题的理解难度,并且对学生提出的这3个问题也难以回答.基于这个原因下文从函数图像斜率和电路两个角度对学生提出的3点疑问展开分析研究.
2 函数图像斜率的数学分析


图2 函数图像斜率
3 电学元件U-I曲线两种斜率的物理分析

表示该状态下电学元件在电路电流发生微小变化ΔI时电压U的瞬时变化快慢或者变化趋势,由电学元件的实际工作点决定[7],称为电学元件在该工作状态下的动态(交流)电阻[6].
对于问题3的分析,如图3所示,在线性元件的U-I曲线上任意一点A与坐标原点O的割线斜率和A点的切线斜率相等,即线性原件在A点的静态电阻和动态电阻相等,因此对线性元件在A点的静态电阻和动态电阻既可以直接利用U-I曲线的割线斜率(或部分电路欧姆定律)求解,也可利用U-I曲线A点切线斜率求解.
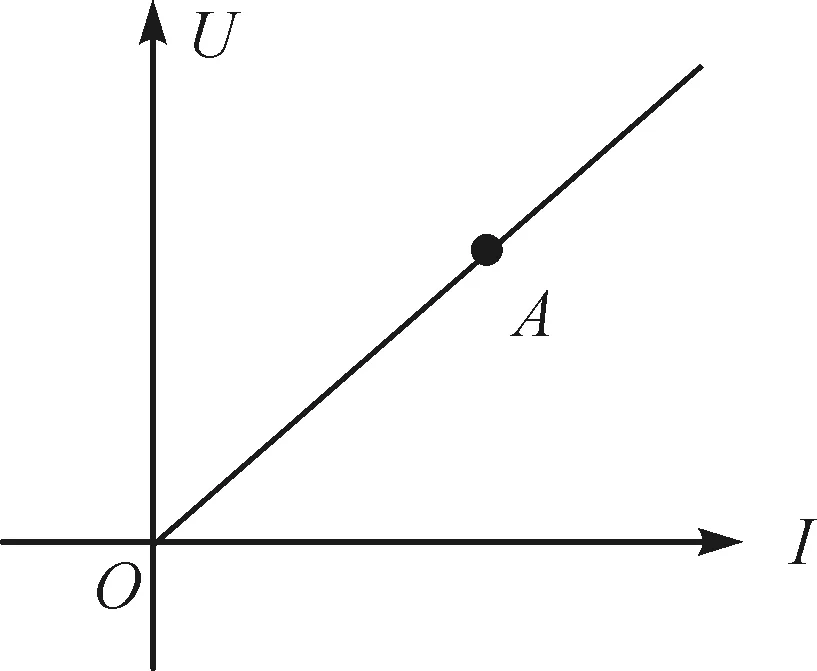
图3 线性元件U-I曲线
如图4所示,在非线性原件的U-I曲线上任意一点A与坐标原点的割线斜率和A点的切线斜率不相等,即非线性原件在A点的静态电阻和动态电阻不相等,且二者均由非线性原件的实际工作点决定,因此对于非线性元件在A点的静态电阻可利用割线斜率(或部分电路欧姆定律)求解,其动态电阻可以直接利用曲线切线斜率求解也可利用闭合电路欧姆定律确定电学元件的工作点后再进行求解.

图4 非线性元件U-I曲线
4 应用U-I曲线斜率讨论上述典例问题
在应用U-I曲线斜率求解电阻问题时,由于线性元件和非线性元件电阻的不同特点.首先要明确求解电阻是线性元件还是非线性元件,以及所求解电阻是静态电阻还是动态电阻,然后再根据相应电阻的处理方法进行求解.下文应用U-I曲线斜率对上述典例1的求解过程进行分析讨论.
E=U1+I(R2+r)
则
保持不变.电压表测量外电路电压,外电路整体为非线性元件,同理可得保持不变.电压表测量定值电阻R2两端的电压,其中表示线性元件R2的动态电阻,其动态电阻和静态电阻相等,根据部分电路欧姆定律得U2=IR2,则保持不变,故选项C正确.
5 例析U-I曲线斜率求解电阻的应用
【典例2】如图5所示,电源电动势E,内电阻恒为r,R是定值电阻,热敏电阻RT的阻值随温度降低而增大,C是平行板电容器.闭合开关S,带电液滴刚好静止在C内.在温度降低过程中,分别用ΔI,ΔU1,ΔU2和ΔU3表示电流表、电压表、电压表和电压表示数变化量的绝对值.关于该电路工作状态的变化,下列说法正确的是( )
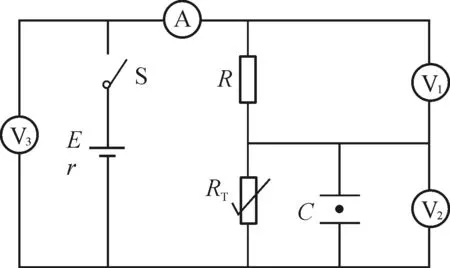
图5 典例2动态电路图
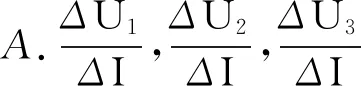

C.带电液滴一定向下加速运动
D.电源的工作效率一定变大
解析:电压表测量电阻R两端电压,表示线性原件R的动态电阻,根据部分电路欧姆定律得U1=IR,则即保持不变;电压表测量热敏电阻RT两端电压,表示非线性原件RT的动态电阻,根据闭合电路欧姆定律确定元件工作点得
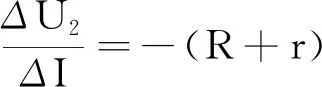


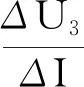
得热敏电阻RT两端电压U2增大,电容器C中场强增大,电场力增大,带电液滴向上加速运动,选项C错误;电源的工作效率
温度降低,热敏电阻RT增大,电源的工作效率η增大,选项D正确.
【典例3】硅光电池是一种太阳能电池,具有低碳环保的优点.如图6所示,图线a是该电池在某光照强度下路端电压U和电流I的关系图像,图线b是某电阻R的U-I图像.当它们组成闭合回路时,下列说法正确的是( )
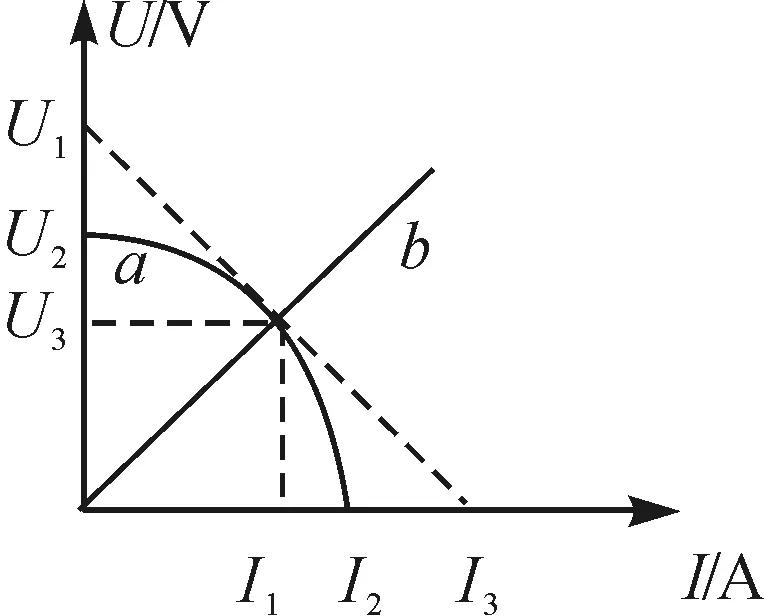
图6 典例3硅电池U-I曲线

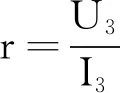
C.硅光电池内阻消耗的热功率Pr=U2I2-U1I1
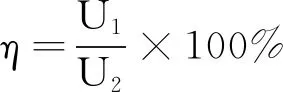
解析:硅光电池是非线性元件,其静态电阻由硅光电池和电阻R组成闭合回路时二者U-I曲线的交点(工作点)决定,根据U-I曲线的割线斜率求得
或者根据闭合电路欧姆定律确定工作点得
U2=U1+I1r

Pr=P总-P出=U2I1-U1I1
选项C错误;硅光电池效率
选项D正确.
通过以上典例2和典例3对运用U-I曲线割线、切线斜率求解电阻过程的详细分析,在培养学生掌握应用U-I曲线斜率求解电阻方法的同时,也有助于学生对U-I曲线两种斜率物理含义的深入理解.
6 结束语
文章对习题教学中学生提出的3点疑问层层递进展开分析,从数学角度给出函数图像割线斜率和切线斜率的数学意义,并将其推广到动态电路电学元件的伏安特性曲线中,以此为基础确定出电学元件U-I曲线中割线和切线斜率的物理含义,弥补了目前教学过程中部分教师和学生对U-I曲线斜率认识的不足,对整个教学效果的提升也有促进作用.通过案例分析如何运用U-I曲线割线和切线斜率对电阻问题实现求解,在培养学生如何利用图像斜率求解物理问题的同时,也进一步加深了学生对U-I曲线两种斜率的理解.

