规范格式 踩点得分

陆松

对于一些比较简单的几何证明题或计算题，大部分同学往往都会做，但却得不到满分。究其原因，主要是几何语言书写格式不规范，步骤不正确等。因此，我们要做的就是在解题时规范几何语言书写格式，明确得分点。

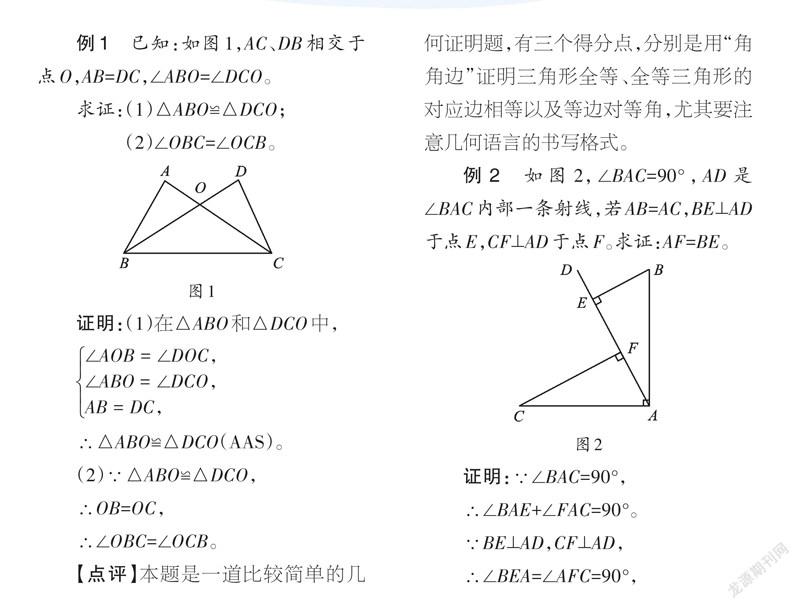
例1 已知：如图1，AC、DB相交于点O，AB=DC，∠ABO=∠DCO。

求证：（1）△ABO≌△DCO;

（2）∠OBC=∠OCB。

证明：（1）在△ABO和△DCO中，

[∠AOB=∠DOC，∠ABO=∠DCO，AB=DC，]

∴△ABO≌△DCO（AAS）。

（2）∵△ABO≌△DCO，

∴OB=OC，

∴∠OBC=∠OCB。

【點评】本题是一道比较简单的几何证明题，有三个得分点，分别是用“角角边”证明三角形全等、全等三角形的对应边相等以及等边对等角，尤其要注意几何语言的书写格式。

例2 如图2，∠BAC=90°，AD是∠BAC内部一条射线，若AB=AC，BE⊥AD于点E，CF⊥AD于点F。求证：AF=BE。

证明：∵∠BAC=90°，

∴∠BAE+∠FAC=90°。

∵BE⊥AD，CF⊥AD，

∴∠BEA=∠AFC=90°，

∴∠BAE+∠EBA=90°，

∴∠EBA=∠FAC。

在△ACF和△BAE中，

[∠AFC=∠BEA，∠FAC=∠EBA，AC=BA，]

∴△ACF≌△BAE（AAS），

∴AF=BE。

【点评】本题主要考查了全等三角形的判定和性质。在证明三角形全等时，关键是要找到证明三角形全等的三个条件。由∠BEA和∠AFC这两个直角可得到其中一个条件∠BEA=∠AFC=90°，这是一个得分点;由∠BAC和∠BEA这两个直角可间接推出另一个条件∠EBA=∠FAC，这也是一个得分点。在证明过程中，能够由∠BAC=90°推出∠BAE+∠FAC=90°，由∠BEA=90°推出∠BAE+∠EBA=90°，可分别得到相应的分数。

例3 如图3，将一张长方形纸片ABCD沿E折叠，使C、A两点重合。点D落在点G处。已知AB=4，BC=8。

（1）求证：△AEF是等腰三角形;

（2）求线段FD的长。

（1）证明：∵四边形ABCD是矩形，

∴AD∥BC， ∴∠FEC=∠AFE。

∵折叠，则∠FEC=∠AEF，

∴∠AEF=∠AFE，

∴AE=AF，

∴△AEF是等腰三角形。

（2）解：∵四边形ABCD是矩形，

∴AD=BC=8，CD=AB=4，∠D=90°。

设FD=x，则AF=AD-FD=8-x。

∵折叠，则FG=FD=x，AG=CD=4，∠G=∠D=90°。

在Rt△AGF中，FG2=AF2-AG2，

即x2=（8-x）2-42，解得x=3，

∴FD=3。

【点评】本题主要考查了矩形的性质、平行线的性质、图像的折叠、等腰三角形的判定定理以及勾股定理等。第（1）问中，由平行和折叠得角相等是一个得分点;通过等量代换，可得到∠AEF=∠AFE，这也是一个得分点。第（2）问中，设FD=x，借助矩形的性质和图像的折叠，可得到△AGF是直角三角形，∠G=90°以及△AGF各边的长度表达式，这是一个得分点;利用勾股定理建立方程，计算正确，即可解得FD的长度，拿到满分。我们在解这道题的时候如果遇到困难，即第（1）问没有证明出来，也可直接跳过去做第（2）问，不受影响。