我“运动” 我快乐
张晓东
在初中數学中,代数有式子的恒等变形,几何有图形的变换,但其本质都是在变化中存在不变的量。图形变换是初中数学研究图形经常会碰到的问题,是几何构图的一种常见方法。初中阶段我们经常用到的变换有平移、旋转以及翻折,这三种变换贯穿初中几何研究,是几何图形学习的重点,也是难点。
一、三角形的平移“运动”
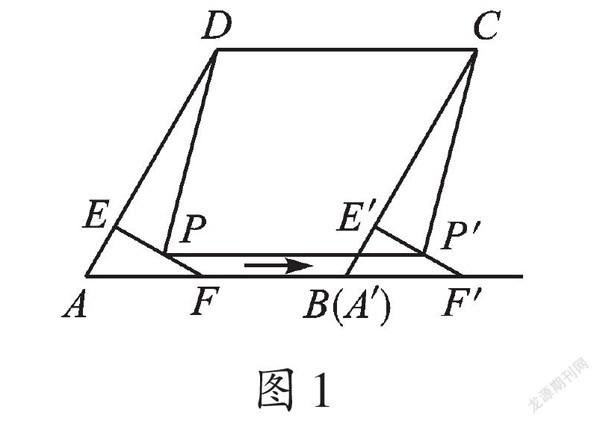
例1 如图1,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点。过点F作FE⊥AD,垂足为E。将△AEF沿点A到点B的方向平移,得到△A'E'F'。设P、P'分别是EF、E'F'的中点,当点A'与点B重合时,求四边形PP'CD的面积。
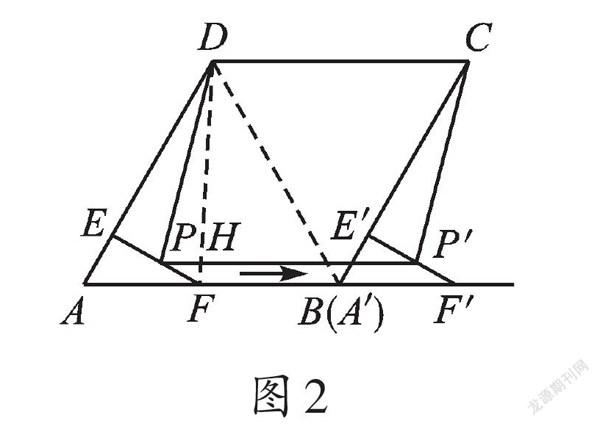
【思路点拨】由已知条件,△AEF沿点A到点B的方向平移,得到△A'E'F',且P、P'是对应点,再根据平移的性质可知PP'=AB=CD=AD=8,PP'∥AB∥CD,从而四边形PP'CD是平行四边形,于是可以考虑用平行四边形的面积公式来计算面积。又由菱形ABCD,F是AB的中点,∠A=60°的条件,联想到等腰三角形“三线合一”。因此,连接DF、DB,DF交PP'于点H(如图2),可证明DF⊥PP',求出DH即可计算出四边形PP'CD的面积为[28√3]。
【评注】平移变换是在平面内将一个图形沿着一个方向平行移动得到另一个图形的几何变换。平移变换只是改变了图形的位置,而图形的大小和形状是不会改变的,因而图形上各点在移动的过程中方向不变(即平行)、距离不变(即线段相等),平移前后的两个图形是全等图形。同学们如果掌握了这些平移的本质,那么解决三角形平移问题也就得心应手了。
二、三角形的旋转“运动”
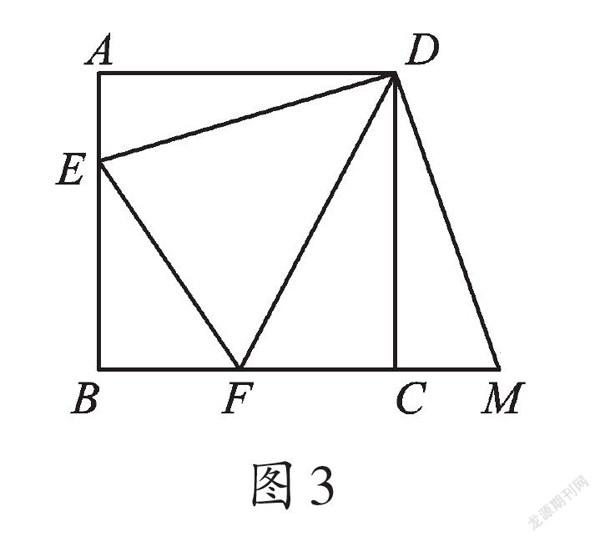
例2 如图3,正方形ABCD的边长为3,E、F分别是AB、BC边上的点,∠EDF=45°,连接EF。将△DAE绕点D逆时针旋转90°得到△DCM。若AE=1,求线段EF的长。
【思路点拨】由旋转的性质可得DE=DM,CM=AE,∠EDM=90°。结合已知条件∠EDF=45°,可得∠FDM=45°,再由DF=DF,故△EDF≌△MDF,得FM=EF。不难发现Rt△EFB的三条边中,EB=AB-AE=2是已知的,EF、BF两边之间存在数量关系,所以可以根据勾股定理列方程求出EF。设EF=x,则FM=EF=x。因为AE=1,所以CM=1,可得FC=FM-CM=x-1,再根据正方形边长为3,得BF=3-FC=4-x,通过列方程可求出EF=2.5。
【评注】旋转变换是在平面内将一个图形绕着某个定点顺时针或逆时针旋转一定的角度后得到另一个新的图形。在解答三角形旋转这种类型的数学问题时,同学们要注意掌握旋转变换的性质,充分利用旋转变换的基本特征:旋转前后两个三角形是全等三角形,而且在旋转过程中所有的旋转角都是相等的。我们要善于找到旋转中的这两个不变的元素,以此探求出问题的解决途径。
三、三角形的翻折“运动”
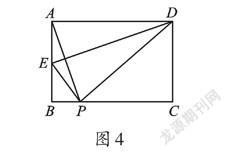
例3 如图4,矩形ABCD中,AB=8,AD=12。将矩形折叠,使点A落在点P处,折痕为DE。若点P恰好在边BC上,连接AP,求[AP/DE]的值。
【思路点拨】由已知条件△ADE沿DE翻折,根据翻折的性质可得对称点连线AP与对称轴DE互相垂直,另外还能得到∠ADE=∠EDP。题目要我们求[AP/DE]的值,可以考虑通过寻找和AP、DE两条线段相关的两个相似三角形来解决。Rt△DAE中,AP⊥DE,所以∠ADE=∠EAP,故Rt△DAE∽Rt△ABP。又因为AB=8,AD=12,利用相似三角形性质求出[AP/DE]=[2/3]。
【评注】翻折变换又称轴对称变换,是指在平面内,以某直线为对称轴,将某一图形沿着这条对称轴翻折而得到另一个新的图形。翻折变换仅仅是图形位置发生了改变,其图形的大小保持不变。同学们在解题时,一方面要弄清翻折后图形中不变的元素,结合全等三角形性质,使问题得以顺利解答;另一方面要注意翻折中对称轴与对称点连线的垂直平分关系及角度的倍分关系。

