基于SoC FPGA硬件并行化计算的配电网电压控制技术

党皓天， 刘东， 陈飞， 赵现平， 刘斯扬， 王宏宇

(1. 上海交通大学电子信息与电气工程学院，上海 200240；2. 云南电网有限责任公司，云南 昆明 650011；3. 江苏金智科技股份有限公司，江苏 南京 211106)

0 引言

电压越限问题是影响配电网电能质量的关键问题。在低碳背景下，越来越多的分布式电源(distributed generator,DG)接入配电网。相比于传统配电网，高DG渗透率下的配电网电压具有更大的波动性[1—3]，这对配电网电压的控制实时性提出了更高要求，IEEE 1547标准对电压越限时间作出了明确限制[4]。

DG自身也是一类可调资源[5—7]，如何充分利用包含DG在内的可调设备是配电网电压调节的关键。然而，不同可调设备的电气特性不同[8]，对不同设备的协同处理极大提高了电压调节的计算难度。另外，随着可调设备接入数量的增加，电压调节所需求解的变量个数也随之增多，传统中心集中式计算方式所需的求解时间大幅增加，这与电压控制所要求的实时性相互矛盾。因此，电压控制正在向边缘计算发展，在边缘节点对其负责的附近区域内的可调设备出力进行计算，既能减少求解变量的数量，又能降低网络传输的时延。

目前，含多种DG的配电网电压控制方式主要分为2类。第一类为电压分区控制方式。该方式一般利用相应规则对系统节点进行区域划分，若某节点电压越限，则由区域内的可调设备调整出力使电压恢复正常[9]，一般适用于规模较大、无功设备充足的配电网。分区划分依据是研究重点，文献[10—12]针对不同场景提出了不同的分区划分依据，取得了较好的应用效果。在分区的基础上，另有文献提出了分层概念。文献[13—14]将控制区域划分为自治控制区域与协调控制区域两部分，电压越限问题由自治控制区域和协调控制区域协同解决。电压分层分区控制策略虽然具有无需迭代计算、响应快速的优势，但其计算只针对某特定区域，忽略或较少考虑了与其他区域的联系，因此无法获得全局最优解。第二类电压控制方式是对无功优化问题直接进行求解，这是一种基于最优化理论的控制方式，一般适用于规模较小、设备较简单的配电网。诸多研究通过启发式算法直接求解[15—17]，另有研究采用二阶锥松弛方法凸化原始非凸优化模型。文献[18]利用二阶锥松弛变换，提出基于等值单相配电网的无功优化方法。文献[19]提出适应三相不平衡主动配电网无功优化的二阶锥松弛模型。此外，文献[20—21]求解非凸非线性的无功优化问题时，采用线性化近似的潮流方程。上述方式虽然可以得到近似全局最优解，但在软件层面计算复杂，加之边缘终端算力不足，导致无法满足电压控制的实时性要求。

在边缘计算下，同时满足区域求解全局性和实时性的核心在于提高边缘终端算力。然而，受限于成本，终端的中央处理器(central processing unit,CPU)和内存资源配置无法达到中心服务器级别，纯软件计算效率提升有限。除此之外，诸多边缘计算研究着眼于利用硬件辅助计算，例如利用现场可编程门阵列(field programmable gate array,FPGA)协助CPU计算[22]。FPGA适用于并行计算，其并行计算优势在录波系统[23]、神经网络[24]、视频检测跟踪[25]等方面均已得到验证。

片上系统现场可编程门阵列(system on chip field programmable gate array,SoC FPGA)可认为是CPU与FPGA的结合，其在计算中可充分利用FPGA的并行计算优势与CPU的通用计算功能，有效提升计算效率。考虑边缘计算场景下的电压控制，文中提出基于SoC FPGA的电压控制策略。为兼顾控制的全局性与高效性，提出一种简化的无功优化模型，同时设计并实现了适用于FPGA计算的改进并行遗传算法，为提升边缘侧电压控制速度提供有效的解决方案。

1 适用于FPGA计算的电压控制模型与算法

不同于中心集中式控制，文中的电压控制策略面向边缘侧，控制对象为一条馈线上所有节点的电压，控制方式为边缘终端计算后的就地控制。馈线虽只是配电网的一部分，但可视为小型配电网，针对配电网的无功控制模型与算法也可以应用于单一馈线。

1.1 适用于FPGA计算的简化电压控制模型

电压控制可视为电力系统无功优化问题。当系统中某一节点电压越限时，通过调节系统中可调的无功设备如储能设备、电容器组和DG等，调节系统的无功分布，从而调节节点电压。

无功优化的目标函数一般为系统节点电压偏移量最小或系统网损最小[26]。文中以系统节点电压偏移量最小为目标函数。约束条件包含等式约束和不等式约束。等式约束为潮流平衡约束。

(1)

式中：Pi，Qi分别为节点i的注入有功功率和无功功率；Ui，Uj分別为节点i和节点j的电压；Gij，Bij，θij分别为节点i和节点j之间的电导、电纳和电压相角差；H为系统节点编号集合；ΔQi为节点i可调无功设备出力；QDG,i为节点i的DG出力；kC,i，QC,i分别为节点i投入电容器组的组数和单个电容器组的出力，kC,i为非负整数。

不等式约束包括节点电压约束、节点功率约束、DG和电容器组出力约束。

该无功优化问题即是求解得出一组可调无功设备出力，在满足等式和不等式约束条件下，使得目标函数值最小。对于此非凸非线性优化问题，即使电压控制目标仅为1条含多种DG的馈线，也需较长的计算时间，因此需要对求解模型进行适当简化，并对算法进行并行设计。

式(1)所示的潮流平衡计算需要多次迭代，若用FPGA进行迭代计算，则所需输入、输出操作较多。同时，此计算过程涉及大量三角函数和复数计算，所需FPGA计算资源较多，会大幅增加计算时间。文中重点考虑DG出力对电压幅值的影响，在出力发生微小变化时可近似认为潮流计算中的雅可比矩阵恒定。在工程化运行允许精度范围内，该近似处理可大大提升电压控制的实时性。

近似的功率平衡可由电压灵敏度矩阵表示。电压灵敏度矩阵反映了电力系统某节点的单位功率变化量对该系统所有节点电压的影响，可由潮流平衡方程推导而来。根据实时电气数据流和系统网络参数，有：

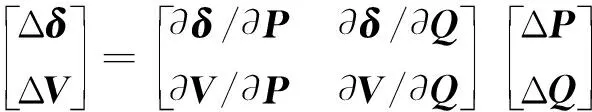
(2)

式中：P,Q分别为各节点注入的有功功率和无功功率；V,δ分别为各节点电压幅值和相角；∂V/∂P,∂V/∂Q为电压灵敏度子矩阵。

文中采用可调无功设备调整无功出力，进而调整电压，可认为ΔP=0。因此电压灵敏度矩阵为：

S=∂V/∂Q

(3)

S反映了节点电压变化量对无功功率变化量的灵敏程度。S为恒定矩阵，通过S可直接近似求得某节点无功功率的变化量对各节点电压的影响。式(1)中的潮流约束条件可简化为：

ΔV=SΔQ

(4)

即：

(5)

式中：n为节点个数。

无功优化问题即是对式(5)中的无功出力进行求解。式(5)中，QC,i为已知量，因此无功优化问题可转化为对[QDG,1kC，1…QDG,ikC,i…QDG,n-1kC,n-1]T的求解。

1.2 适用于FPGA计算的改进并行遗传算法

对于上述无功优化问题，传统求解算法包括电压分区控制算法与启发式优化求解算法。前者求得的是局部解，后者求得的是全局解。文中综合利用这2种算法，提出一种适用于FPGA快速求解的改进并行遗传算法。

1.2.1 传统无功优化求解算法

电压分区控制时，首先定义一个临界量ΔUth，对于无功电源的单位注入无功功率改变量，若某节点电压改变量高于ΔUth，则将此节点纳入该无功电源的调压域。当系统某节点电压越限时，仅调节该节点所属调压域内的无功电源即可。电压分区控制方法具有快速、无需多次迭代计算等优势，但其忽视了调压域外无功电源的作用，因此得到的仅是粗略的局部解，无法获得全局最优解。

求取无功优化问题的全局最优解，一般采用粒子群算法、和声算法、遗传算法等启发式算法搜索全局最优解或近似全局最优解。因遗传算法具有收敛速度快、适用于并行计算的优势，此处以遗传算法为例进行介绍，后续将改进的遗传算法在FPGA上实现，利用FPGA并行求解无功优化问题。

针对电压控制问题，经典遗传算法求解步骤为：(1) 生成初始化种群，每个个体为无功出力向量；(2) 进入迭代计算过程，进行选择、交叉、变异操作，并保证生成的新个体满足功率要求；(3) 进行适应度计算，将生成的新个体代入式(5)计算目标函数值(遗传算法中的适应度值)并存储；(4) 一代遗传完毕，若不满足求解要求，则回到步骤(2)重复迭代过程。

遗传算法虽然可以计算出较为接近的全局最优解，但计算中有多次迭代过程，影响计算效率。

1.2.2 改进并行遗传算法

考虑到遗传算法本身编码与求解方式具有并行性，适用于FPGA求解加速，因此无功优化问题求解主体选取遗传算法。此外，为同时满足全局性和实时性要求，文中对遗传算法改进如下。

(1) 种群初始化过程引入电压分区控制策略。由于遗传算法初始种群的选取对算法的收敛性和效率影响很大，完全随机的初始种群会导致收敛效果不佳。考虑到配电网自身无功出力对电压影响的特征，理论上的全局最优解与电压分区控制算法生成的局部最优解相差较小。因此，为提高收敛速度，将初始种群中的一部分设置为电压分区控制直接所得的个体，其余部分随机产生。

(2) 迭代计算过程中应用种群级和基因级的并行求解。种群级的并行是将一个大种群划分为多个小种群，多个小种群并行地进行遗传计算，只有经过一定的代数后种群间才进行交流。基因级的并行是指对于同一向量的不同位点可以同时操作，这在迭代过程中的交叉、变异和适应度计算操作中都有大量应用。与CPU的串行执行特性不同，FPGA本质是专用的硬件电路，种群级和基因级的并行都可以通过增加硬件资源实现。

(3) 迭代计算过程流水线化。遗传算法中的选择、交叉、变异和适应度计算操作按顺序组成了一个执行周期。FPGA设计中不同操作对应不同实际硬件模块，采用流水线化的计算方式可有效降低模块空闲率，提升计算效率。

2 基于SoC FPGA的电压控制处理流程

2.1 SoC FPGA处理平台

完整的电压控制流程需要CPU与FPGA的协同计算，SoC FPGA为嵌入式系统提供了一种完全可编程的SoC，即异构的片上系统结构，将通用处理器与可编程逻辑相结合。SoC FPGA内部架构可分为两部分，分别为处理器系统(processing system,PS)和可编程逻辑(programmable logic,PL),两者之间通过高速接口通信。该架构支持在PL部分进行硬件逻辑设计，同时在PS部分进行软件设计。

2.2 电压控制处理流程设计

SoC FPGA是计算与控制中心，文中设计其数据处理架构如图1所示。在处理中，PS侧首先通过千兆以太网口接收配电网实时电气信号并进行潮流计算、S计算，之后将S计算结果通过高级可扩展接口(advanced extensible interface，AXI)实时更新至PL侧的块存储器(block random access memory,BRAM)。BRAM为PS侧与PL侧数据交互的桥梁。

图1 SoC FPGA数据处理架构Fig.1 Data processing architecture of SoC FPGA

同时，PS侧对S进行实时计算，而非检测到电压越限后才进行计算，原因是S的计算耗时较多，若在检测到电压越限后再进行计算则会大大增加无功优化计算时间。S在短时间内变化很小，因此无功优化计算时，利用上一个时间点的S可以保证计算准确性，且不必花费重新计算的时间。此处S的计算周期为2 s。PL侧在收到计算指令后可以直接从BRAM中获取S数据。

PS侧检测到电压越限后，会立刻通过AXI将实时节点电压数据、电压与功率约束条件和生成的部分初始化种群传输至BRAM中固定的对应地址，同时触发PL侧并行计算模块基于遗传算法进行无功优化计算。PL侧计算结束后，通过中断的方式将最终计算结果传输至PS侧。PS侧根据此计算结果决定发出无功调整指令或将结果上报给中心云端服务器。上述PS侧和PL侧协作计算的工作流程如图2所示。

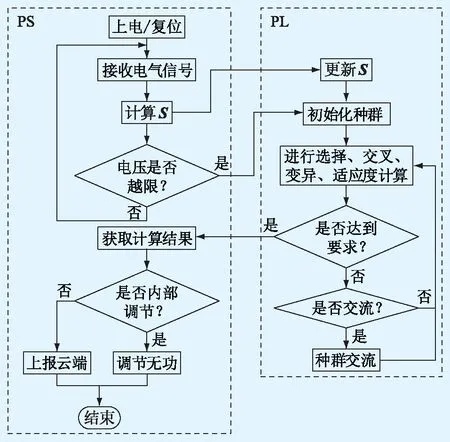
图2 PS侧与PL侧协作计算流程Fig.2 Collaborative calculation process of PS side and PL side

3 适用于FPGA计算的并行遗传算法设计

在设计时，S为实时计算所得，不会阻塞求解过程，因此影响无功优化求解时间的最主要因素是遗传算法效率。文中在FPGA上分模块设计应用于电压控制求解的改进遗传算法。

3.1 硬件架构设计

FPGA上的硬件设计一般采用自顶向下的模块化设计。将遗传算法的各个步骤设计为各个硬件模块，并根据数据流通逻辑将其连接。PL侧模块化系统结构设计如图3所示。

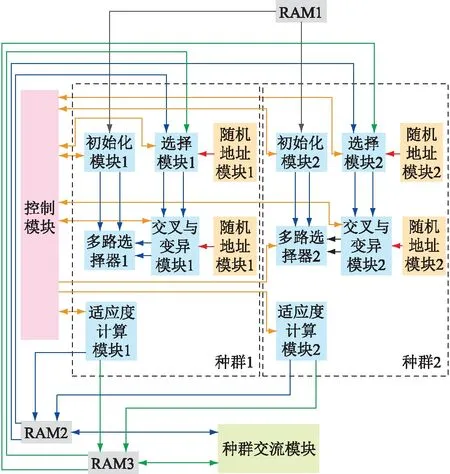
图3 并行遗传算法系统结构(并行度为2)Fig.3 System architecture of parallel genetic algorithm(degree of parallelism is 2)

图3中，控制模块是核心，各模块的正常工作均依赖于控制模块的控制信号。RAM1的存储内容为PS侧计算出的S，即各节点的实际电压、功率，电压约束与功率约束。RAM2、RAM3分别存储种群个体与对应适应度。种群交流模块通过与RAM2、RAM3交互实现不同种群间的交流。其余模块均负责某个种群进化过程中的某一步骤，各模块数量与并行进化种群数量一致。

3.2 编码设计

系统可调无功设备包括各节点DG及电容器组。前者为连续变量，后者为离散变量。对于包含DG或电容器组的节点，用11 b的编码表示该节点的DG出力，首位为符号位，对应于-1 024～1 024 kvar的可调量；用5 b的编码表示电容器组投入组数，首位同样为符号位，对应于-16～16组的可投切量。以上变化量均可覆盖节点DG出力或电容器组投入组数的取值范围。单一节点对应变量编码如图4所示。

图4 单一节点对应编码格式Fig.4 Encoding format for a single node

假设在配电网系统中存在T个节点具有无功调节能力，则遗传算法种群中的每个个体均可表示为16T个数字相连，即[QDG,1kC,1…QDG,ikC,i…QDG,TkC,T]T对应的编码位数为16T。

3.3 模块化硬件设计要点

基于软件求解的遗传算法在文献[15,23]中已有详细说明，此处重点介绍遗传算法的FPGA求解相较于软件求解的不同之处，以及针对电压调节场景的适应性改进。

(1) 设计控制模块，保证硬件系统有序正常工作。不同于CPU中天然的串行化处理，FPGA中不同模块的串行化工作需要有限状态机的支持。控制模块即通过适用于遗传算法的有限状态机实现与其他模块的信号交互。

将每个种群的进化过程分为7个状态。其中空闲和停止分别表示复位和结束信号。另外5个状态为工作状态，分别为种群初始化、选择状态、交叉变异、适应度计算和种群交流。状态转换如图5所示。

图5 控制模块有限状态机Fig.5 Finite state machine in control module

(2) 在初始化模块设计中引入电压分区控制思想，提高遗传算法收敛速度。初代种群的选取对遗传算法的收敛性影响很大。分区控制策略给出的无功调整解是一个较为粗略的解，但结合实际情况可知，该解与最终的全局最优解较为接近，因此可将其作为初代种群的一部分，提高算法收敛速度。

文中设置初代种群中25%的个体由电压分区控制策略给出，另外75%的个体在初始化模块中随机产生。以此设置，既可以利用分区控制算法的结果提高算法收敛速度，又可以防止算法陷入早熟或局部最优解。

(3) 由于FPGA不善于概率计算，须设计新的选择机制。该机制的实现需要选择模块、存储模块以及随机数生成模块的协同配合。

常用的选择操作为轮盘赌选择和随机联赛选择。轮盘赌选择的核心思想是使更优秀的个体有更大的概率被选中，每个个体被选中的概率为其适应度与种群所有个体适应度之和的比值。随机联赛选择更为简单，随机从种群中选取偶数个个体，两两进行比较，更优秀的个体得以保留。

虽然轮盘赌选择更为合理，但由于FPGA处理小数与概率问题较为复杂，因此文中设计的选择机制基于随机联赛选择，同时吸取了比例选择的思想。该机制依赖存储模块的设置。存储模块每次存储2个新个体及其对应适应度，在存储前对待存储的2个个体适应度进行比较，适应度较高的个体存储于种群的上半部分，适应度较低的个体存储于种群的下半部分。

选择操作中随机选择的个体位置由随机数模块产生，通过对随机数进行修正，使得种群上半部分的个体有更大概率被选出，从而接近轮盘赌的选择结果。随机数生成模块为一个x位线性反馈移位寄存器，如图6所示。

图6 随机数生成模块Fig.6 Random number generation module

(4) 复制硬件电路实现种群的并行进化，并设计种群交流模块负责种群间的交流。种群的并行进化既可以提高遗传算法计算的并行度，又可以独立发展出不同的优良基因片段。而种群交流有助于优良基因的集中，进化出更为优秀的个体。设计中，种群交流表现为某一种群内最优个体对另一种群内最差个体的替换。假设种群进化并行度为m，种群间交流过程如图7所示。

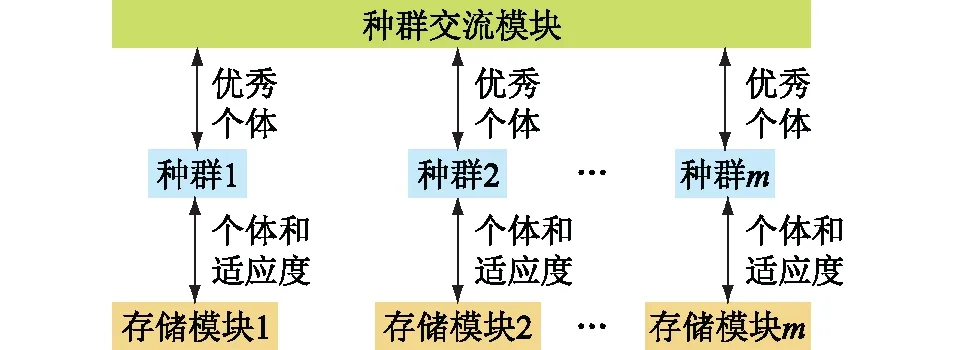
图7 种群间交流过程示意Fig.7 Schematic diagram of the communication process between species

(5) 各模块内部的乘加计算与矩阵计算中，通过增加硬件资源实现基因级的并行。交叉和变异分别采用多点交叉和多点变异操作。对于多点操作，在FPGA中可复制硬件单元实现并行操作。

适应度计算模块是最耗费硬件资源的模块，同时也是通过FPGA并行计算最能提升计算效率的模块。由于交叉变异模块的输出个体已保证功率满足约束条件。因此在适应度计算时仅考虑电压越限问题。文中对于电压约束问题的考虑体现在目标函数惩罚系数分段设计中。当通过S计算所得的某节点电压越限时，该节点对应项的惩罚因子较其他非越限项更大。且电压偏移越多，其惩罚系数越大，导致最终目标函数值越大。经过几代选择后，明显会产生电压越限的个体基因片段会被剔除。

基于以上分析，适应度计算模块仅计算输入个体对应的目标函数值即可，不必考虑约束条件。目标函数值的计算涉及矩阵运算与多个乘加运算，可充分发挥FPGA的并行计算能力。

适应度计算步骤为：将电容器组数映射为无功出力，并与DG出力加和形成无功出力向量；代入式(5)进行计算，求得各节点电压增量与改变后的实际电压；代入目标函数求适应度。

上述步骤中的乘加计算与矩阵计算均可通过堆叠硬件资源并行求解。

4 算例分析

4.1 参数设置

文中以某配电系统衍生的算例为对象进行分析[27]。该算例包含62个节点，共3条馈线，馈线间通过联络线连接。文中面向边缘侧单条馈线进行电压控制，不涉及馈线间的无功支撑，因此选取其中1条馈线为例进行重点分析，其拓扑如图8所示。系统基准电压为10 kV，基准容量为10 MW，各节点电压可接受偏移范围为-0.05～0.05 p.u.，负荷均视为恒定功率负荷。为验证文中所提电压控制策略，对算例修改如下：在节点3、节点5和节点11安装DG，每组DG的无功出力范围为0～600 kvar，每组DG的容量为1 MV·A，每组逆变器的容量为1.2 MV·A。在节点2、节点9分别安装10组电容器，每组电容器容量为25 kvar。

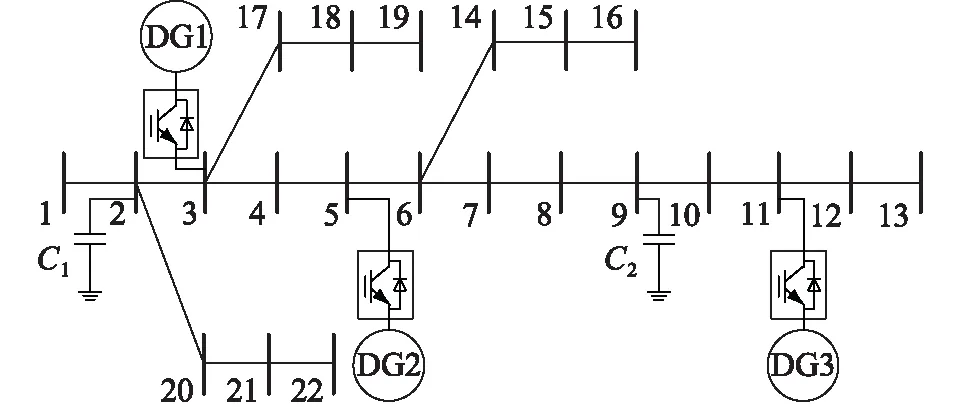
图8 馈线拓扑Fig.8 Feeder topology

设置ΔUth为0.08 p.u.[28]。当某一节点电压变化量同时达到多个可调设备的门槛值时，将其分配至引起其电压变化量最大的可调设备调压域。以此为依据将该系统划分为2个调压域，如表1所示。

表1 调压域划分Table 1 Division of voltage regulation zone

设置个体生成策略为：选取电压越限最严重的节点，由该节点所在调压域内的可调无功设备调整无功出力为主，由调压域外的无功设备出力调整为辅。设调整无功出力总量为恒定值ΔQch，其值为对作用最强的可调无功设备支撑该节点电压抬升至1.02 p.u.或下降至0.98 p.u.所增加或减少的无功值。ΔQch由调压域内出力和调压域外出力两部分组成。设定调压域内可调设备的出力比例分别为0.95ΔQch，0.90ΔQch，0.85ΔQch，0.80ΔQch，保证域内出力占主导地位。在具体分配中，调压域内的出力分配按不同可调设备所在节点的电压灵敏度系数加权分配，调压域外设备的出力随机分配。

FPGA硬件并行化计算的遗传算法相应参数设置如表2所示。SoC FPGA的硬件参数如表3所示。

表2 并行遗传算法参数设置Table 2 Parameters of parallel genetic algorithm

表3 SoC FPGA硬件参数Table 3 Hardware parameters of SoC FPGA

4.2 仿真验证与分析

4.2.1 初始系统状态

文中设计的目的在于兼顾边缘侧馈线电压控制的全局准确性与计算高效性。采用节点电压越下限与节点电压越上限2种场景进行分析，2种场景的初始电压分别如图9、图10中初始电压所示。

记文中SoC FPGA软硬件结合的电压控制方法为方法Ⅰ。将以下3种求解方式与方法Ⅰ进行对比。

方法Ⅱ：电压分区控制方式。由电压分区控制策略直接给出可调设备无功调整量。

方法Ⅲ：纯软件非迭代方式。采用纯软件的计算方式，将FPGA并行化遗传算法求解部分改为软件计算。其他设置不变。

方法Ⅳ：纯软件迭代方式。在方法Ⅲ的基础上，将式(5)电压灵敏度矩阵约束条件改为式(3)的原始潮流平衡约束条件。此时，每次适应度计算均完成一次完整的潮流计算。

以上4种方法具有相同的初始化种群。

4.2.2 全局准确性

应用上述4种方法，电压越下限场景的调压效果和求解结果分别如图9和表4所示，电压越上限场景的调压效果和求解结果分别见图10和表5。

图9 电压越下限场景的调压效果对比Fig.9 Comparison of voltage regulation effects where voltage is lower than lower limit

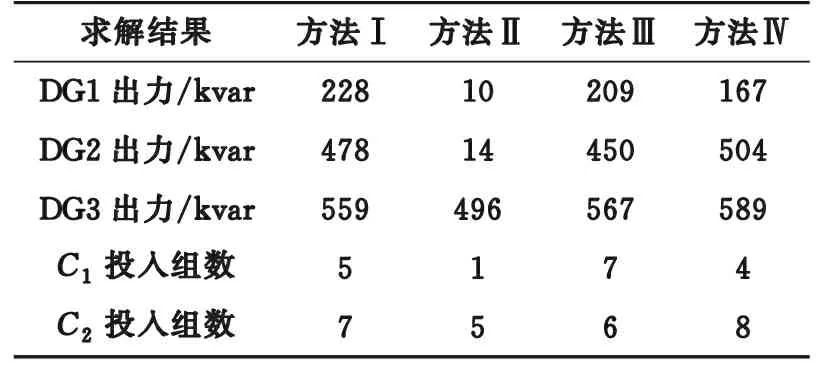
表4 电压越下限场景的4种方式求解结果Table 4 The solution results of four methods in the scenario where voltage is lower than lower limit

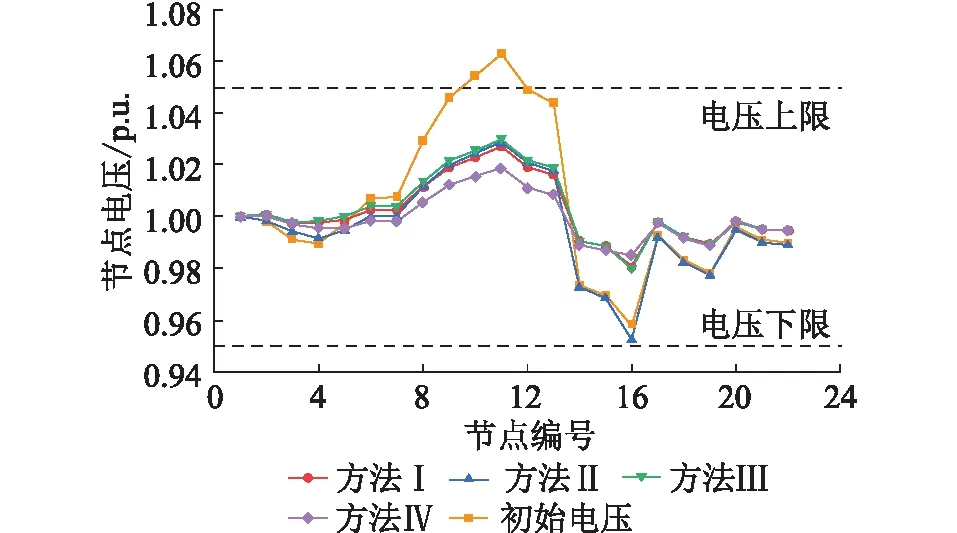
图10 电压越上限场景的调压效果对比Fig.10 Comparison of voltage regulation effects where voltage exceeds upper limit

上述2种场景的求解结果均满足功率约束。方法Ⅰ和方法Ⅲ应用简化模型求解，而方法Ⅱ应用电压分区控制方式求解。由图9和图10可知，2种场景越限节点的电压均可恢复至正常范围内，但对距离越限节点较远的其他非越限节点(例如节点16)的电压调节，方法Ⅰ明显优于方法Ⅱ。因此，相比于方法Ⅱ，方法Ⅰ具有更好的全局性。

表5 电压越上限场景的4种方式求解结果Table 5 The solution results of four methods in the scenario where voltage exceeds upper limit

方法Ⅳ应用原始模型进行求解，将其求解结果与简化模型求解结果进行对比。与原始模型相比，简化模型出于计算效率考虑，将潮流平衡条件线性化，因此用最终近似计算结果代入实际潮流计算时会产生一定的偏差。但考虑电压调整的实时性，相比于此近似计算产生的较小偏差，计算效率的大幅提升具有更大意义。

4.2.3 计算高效性

在保证控制全局准确性的基础上，验证文中所提方法Ⅰ的计算效率优势。将方法Ⅰ的求解效率与方法Ⅲ、方法Ⅳ进行对比，经过随机10次重复验证，统计3种方法的平均求解时间与遗传代数。2种场景的求解效率对比分别如表6和表7所示。

表6 电压越下限场景的求解效率对比Table 6 Comparison of solution efficiency in the scenario where voltage is lower than lower limit

表7 电压越上限场景的求解效率对比Table 7 Comparison of solution efficiency in the scenario where voltage exceeds upper limit

由表6、表7分析可知，方法Ⅳ的求解用时明显大于方法Ⅰ和方法Ⅲ。这是由于方法Ⅳ采用了原始无功控制模型，在遗传算法中对于每个个体的适应度计算都需要完整的潮流计算。每次潮流计算都包括多次迭代过程，极大增加了计算时间。此外，潮流计算的迭代次数不确定，适应度计算的时间也具有较大波动性。因此，方法Ⅳ不具备实时性，这也说明了方法Ⅰ在计算效率上具有明显优势。

进而对比方法Ⅰ和方法Ⅲ可知，对于相同的计算量，方法Ⅰ利用FPGA并行化加速计算的遗传算法，相比于方法Ⅲ的纯软件计算，在计算用时上具有较大优势。在上述2个电压越限场景中，方法Ⅰ相对于方法Ⅲ的计算效率分别提升了2.41倍和2.15倍。最后，实验表明在上述2种场景下，方法Ⅰ的并行加速比分别为1.97，1.71。

综上，在上述2种电压越限场景下，与其他电压控制方法相比，文中利用简化模型、基于SoC FPGA计算的并行遗传算法可以更好地兼顾求解的全局性与高效性。

5 结语

随着越来越多的可控DG接入配电网，传统中心集中式的电压控制计算方式在计算效率与控制实时性上表现出了不足，因此配电网的电压控制向边缘计算发展。为在边缘终端上实现快速电压控制，文中提出并实现了一种基于SoC FPGA的硬件并行化电压控制方法。该方法结合了电压分区控制策略与遗传算法求解方式，正确划分软硬件职责，在软件侧非阻塞式地计算电压灵敏度矩阵，在硬件侧利用FPGA优秀的并行计算能力，加速了优化问题的求解。算例分析对比验证表明，相比于纯软件的计算方式，所提方法可以大幅提高电压控制的实时性。

在更大规模DG接入的配电网系统中，由于其可调可控资源更多，在终端利用FPGA并行化计算的并行度也会相应提高，从而可以更大幅度地提升终端设备的计算效率。随着物联网与通信技术的发展，所提方法由于计算效率的优势，将在配电网电压控制领域具有广阔的应用前景。