基于最优路径选择的网络感知服务组合算法*
余 建,林志兴,余高锋,肖香梅,刘孙发
(1.三明学院 a.网络中心;b.信息工程学院,福建 三明365004;2.物联网应用福建省高校工程研究中心,福建 三明365004)
0 引 言
随着云计算[1]、物联网[2]、移动互联网[3]、大数据[4]等现代信息技术的不断发展,用户(特别是手机用户)需求日益增多,单一的服务已经无法满足,而服务组合技术可将现有的分布式的服务集成为满足用户需求的组合服务[5]。在个性化需求不断扩大的背景下,随着大量的手机APP软件的推出,如何将不同的服务进行组合而又能保障全局网络的服务质量(Quality of Service,QoS),已成为当前亟待解决的问题。同时考虑云服务和网络服务的QoS属性,解决一体化环境下服务组合问题,给出最优的服务组合算法,为不同需求的用户提供点到点服务质量保障,具有重要的理论价值和广阔的应用前景。
针对服务组合优化,许多学者进行了大量的研究。张以文等[6]提出了一种任务粒化算法(Task-granular Algorithm,TgA),用于快速有效地求解大规模服务组合优化问题。张丽娜等[7]在解决海量线上到线下(Online to Offline,O2O)服务环境中,引入社会关系理论,在线上服务组合阶段考虑提高线下服务提供商之间的协作效率,同时优化算法的执行效率。蔡江安等[8]等针对服务组合问题,利用服务组合策略,建立了以时间、实用性、创新性、可靠性等为优化目标的服务组合优化模型;同时通过聚类算法以及对组合服务的关联规则对路径搜索空间进行预处理,大大提高了搜索空间的效率,让知识服务资源能在服务组合中以较短的时间内进行精准定位并与之匹配,较大程度上提高服务组合的性能。
Ergun等人[9]针对双度量QoS选路问题提出了一种性能出色的近似算法,通过选取最优的一个上、下界,引入一个多项式时间的近似测试过程,去不断地缩小上下界之间的距离,把路径搜索问题转化成区间搜索问题,在不断缩小的范围内快速查找最优解。Xue等人[10]提出了一种PeseudoMCPP算法,给出了一种利用路径跳数构建路径搜索空间,可以获得在满足第一维路径权重约束D的情况下,其他维路径权重也都满足于某个约束C。由于Ergun等人提出的算法非常耗时,而Xue等人的算法不能继承已知的结果,因而都难以获得质量更好的求解方案。本文在综合考虑网络服务特点的基础上,结合以上两种算法思路,给出了一种服务最优路径选择算法(Optimal Path Selection,OPS),以解决QoS感知的网络服务组合问题,提升网络服务质量水平,改善用户体验质量。
在某商务出行案例中,如果每一个服务类表示为{(S1,S2,S3,…,St)},按照组合服务对应的主体,我们可分为4个服务实例,即打车平台服务、网上购票、网上订餐、酒店预定,任务粒(抽象服务)表示为{(S1,S2,S3,S4)}。若假设每个任务都有相关候选服务可以实现其所在服务类的功能,但是它们有不同的服务质量,因此,人们会根据候选服务的服务质量选择最优的服务组合方案。
1 相关工作
1.1 QoS感知服务组合定义
服务组合能充分利用目前已有的服务,具有即时、快速和灵活组建分布式松耦合的优势[11]。当网络用户向服务器端请求服务时,服务器端将调用服务组合过程,选择一系列原子服务组件来构建功能复杂的组合服务,以满足网络用户个性化的需求。本文中的服务组合路径包括多个单个服务进行组合[12],即组合服务(也称多目标服务组合、多任务组合服务或综合性服务)。
定义1 可行的服务组合方案。每个服务Si(1≤i≤H),每个服务对应一个原子服务组件SH,假设一个服务组合方案,如在某服务网络中的一条路径p,cv和Ch代表节点v和h的服务能力,ωk为其路径的最小权重,Wk代表约束条件,K为任务S执行的任务次数,如果对于∀v∈p有cv≥Ch,节点不和ωk(p)≤Wk,其中υ∈Sh,1≤h≤H,1≤k≤K,那么路径p是一个可行的服务组合方案。
1.2 服务组合结构转化
服务组合流程包括串行、选择、并行等结构,这些基本结构可以构造出很多结构不同的复杂服务组合流程。在基于功能方面的需求为请求中的每一个功能选择服务之后,服务目录根据用户的QoS要求,在大量候选的服务组合路径流程中选出满足用户要求的最优组合路径。
当用户在每一个任务粒中选对一个候选服务时,根据网络服务中最优组合路径选择原则,云服务器应在最短时间内响应用户需求。由于每个候选服务组合路径包含多种拓扑结构,现有的大多数服务选择算法无法直接处理多种结构,因此在服务选择之前需要对拓扑进行结构转换[13],在这个转化过程中Sa和Sb保持不变。执行完Sa之后,就分别以p1,p2,…,pn概率执行服务S1,S2,…,Sn,然后再执行Sb。ti、ci、ri、thi分别代表的响应时间、代价、可靠性和吞吐量,Fi(x)代表概率响应时间t的概率密度函数,Pi1(x)代表代价c的密度函数,Pi2(x)代表可靠性r的密度函数,Pi3(x)代表吞吐量th′的密度函数,P代表顺序结构转换后的服务S1n的值,计算如下:
(1)
(2)
(3)
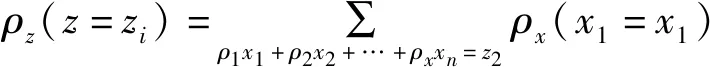
(4)
(5)
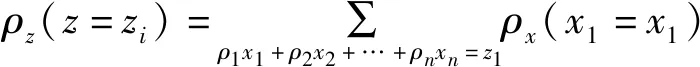
(6)
(7)
(8)
1.3 QoS感知服务组合模型
一个服务组合的流程是[14]:用户先提出自已的业务需求,服务组合根据用户的需求设计一个抽象服务模型,然后在每一个抽象服务所对应的候选服务集合中选择一个服务与之相对应,并把最后所形成的关联服务也即组合服务反馈给用户,该组合一定是满足用户约束且QoS最优的。组合服务是一个组合服务集合,其所包含的组合服务不被其他组合服务支配,它通常被用来提高组合服务选择的效率。
为了找到更优的服务组合路径,我们建立了QoS感知服务组合模型。在服务组合模型中,单一服务通常无法满足用户需求,而需要将多种服务按照顺序组成一条工作流来完成用户请求。在组合服务选择过程中,某个服务通常有多个候选服务[15]提供商。在组合服务集合中,通过不同任务中的候选服务之间存在关联性,再通过OSP算法建立最优路径选择,从而找到一条花费较小的服务组合路径。如图1所示,每个服务Si(1≤i≤H)中有许多原子服务组件Sij(1≤i≤H,1≤f≤F)作为服务组合的候选组件。该感知服务组合模型将网络服务和云服务的QoS参数一并映射在每两个服务之间的边上。对于每一个服务请求,这个服务组合过程将找到一条从服务入口s到服务出口t的路径p。如果该路径p贯穿所有被选中的服务组件,并且满足用户QoS需求,那么它就将作为组合服务(或服务组合方案)返回给用户。
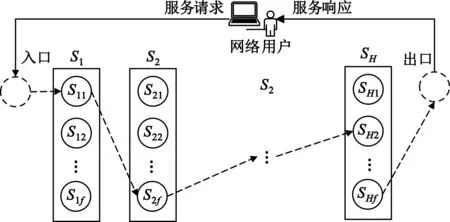
图1 感知服务服务组合模型
1.4 组合服务关联
在本文案例中,出行者打车平台服务、网上购票、网上订餐、酒店预定四个任务粒为云端服务时,则对应的网络质量就可以设定为其关联性服务。
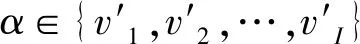
根据文献[16]中所建立关联匹配器的过程及建立过程中所需的符号和对应的含义给出严格的数学定义。考虑到任务间的关联,某些已经完成的任务可能会影响未执行任务与具体服务的对应关系。在图1中,服务S1、S2、S3、S4为候选服务中(S1f,S2f,…,Shf)已完成的任务粒,并且都为一组具体有关联关系的任务粒。服务在选取任务时,首先需要考虑的是与服务具有关联关系的最优服务质量的任务粒。当具有关联关系的服务无法满足用户的需求时,则重新对任务粒进行重选取。关联关系的重选取算法的步骤如下:
Step1 更新服务组合模型的参数。已经完成的任务集为SHf={S1f,S2f,…,Shf},对应完成任务的服务为E(SHf)={S1f,S2f,…,Shf},然后把Shf和E(Shf)间对应关系的参数x1,x2,…,xu设定为1。将集合E(Shf)包含的服务在实际执行过程中的价格与响应时间代入服务组合模型,并把这些服务在组合模型中对应的可靠性设置为1。
Step2 候选服务选择。设一组关联任务集为S1f={S11,S12,…,S1f},它对应的具有QoS关联关系的候选服务集为S2f={S21,S22,…,S2f}。任务集S1f∈S是一组已经完成的任务,对应E(Stf)的服务为E(Stf)={S1f,S2f,…,Stf},然后对于任意一组关联服务,如果满足条Stf∈E(Stf)则进行关联。
Step3 将以上两步得到结果用关联性准则进行关联,再利用服务组合模型参数进行判断,当参数为1时,任务关联;当参数为0时,任务关联失败。
2 基于QoS感知的服务组合算法
2.1 算法设计
在实际场景可承受的范围内,以消耗较少的资源找到近似最优解是完全可行的。根据近似算法[18]理论设计一种求解该问题的网络服务组合近似算法是一种非常可靠有效的方法。因此,结合近似算法思想,本文给出OSP算法,以获得满足用户QoS需求的网络服务组合方案。算法流程图如图2所示。

图2 OSP算法设计流程
网络感知服务组合OSP算法的伪代码如下:
Algorithm OSP
Input:GraphG(V,E,s,t,ω,W,c,C,H,K),Parameterε;
Output:pathp:
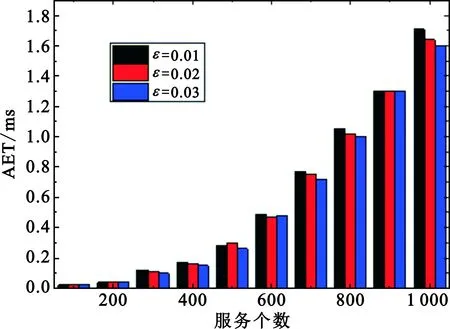
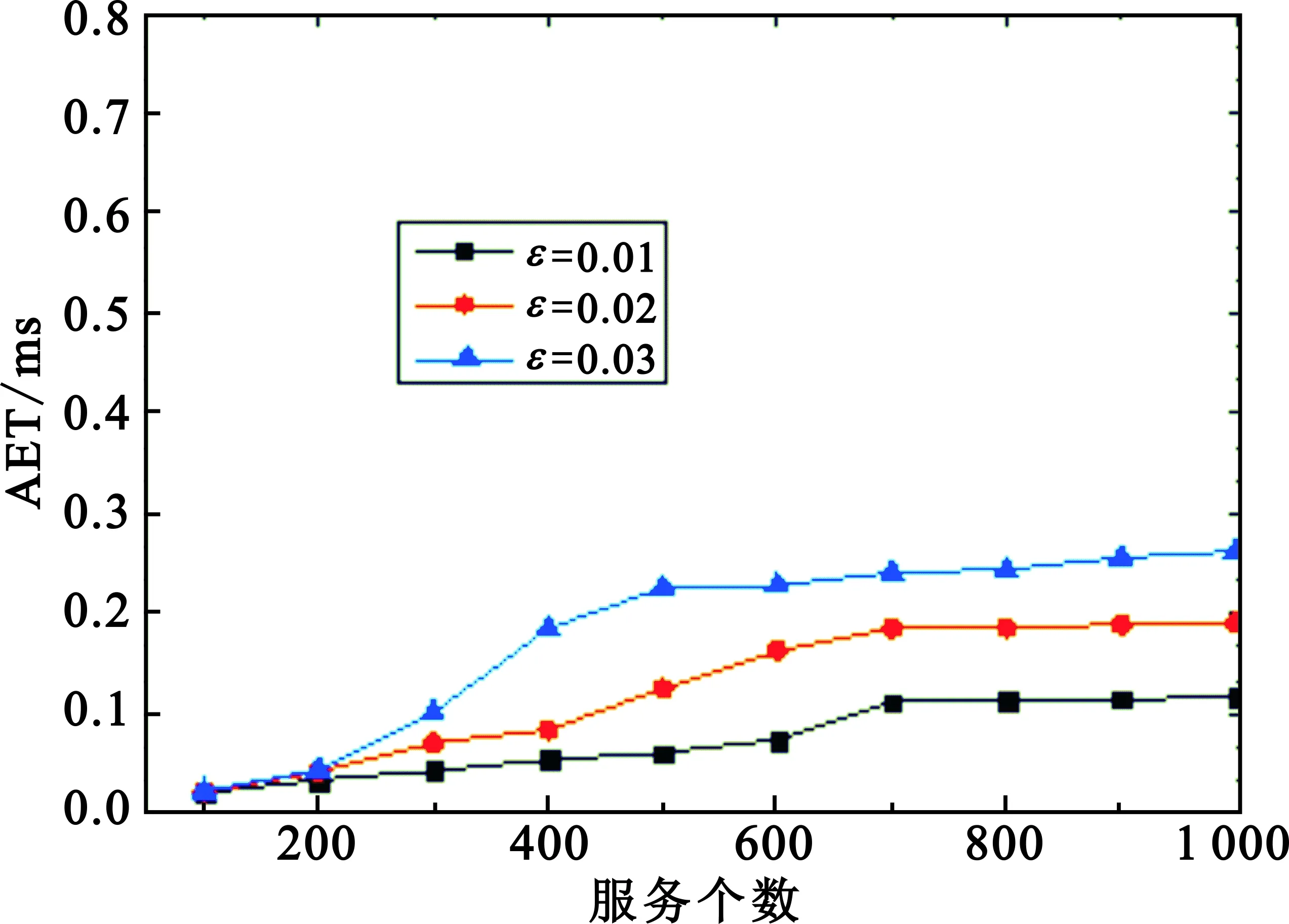
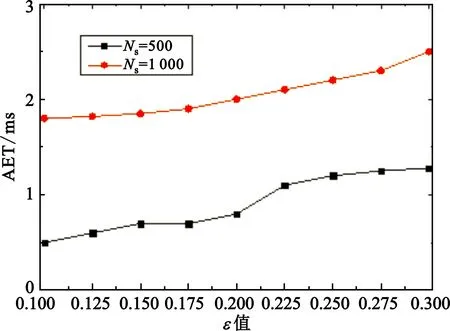
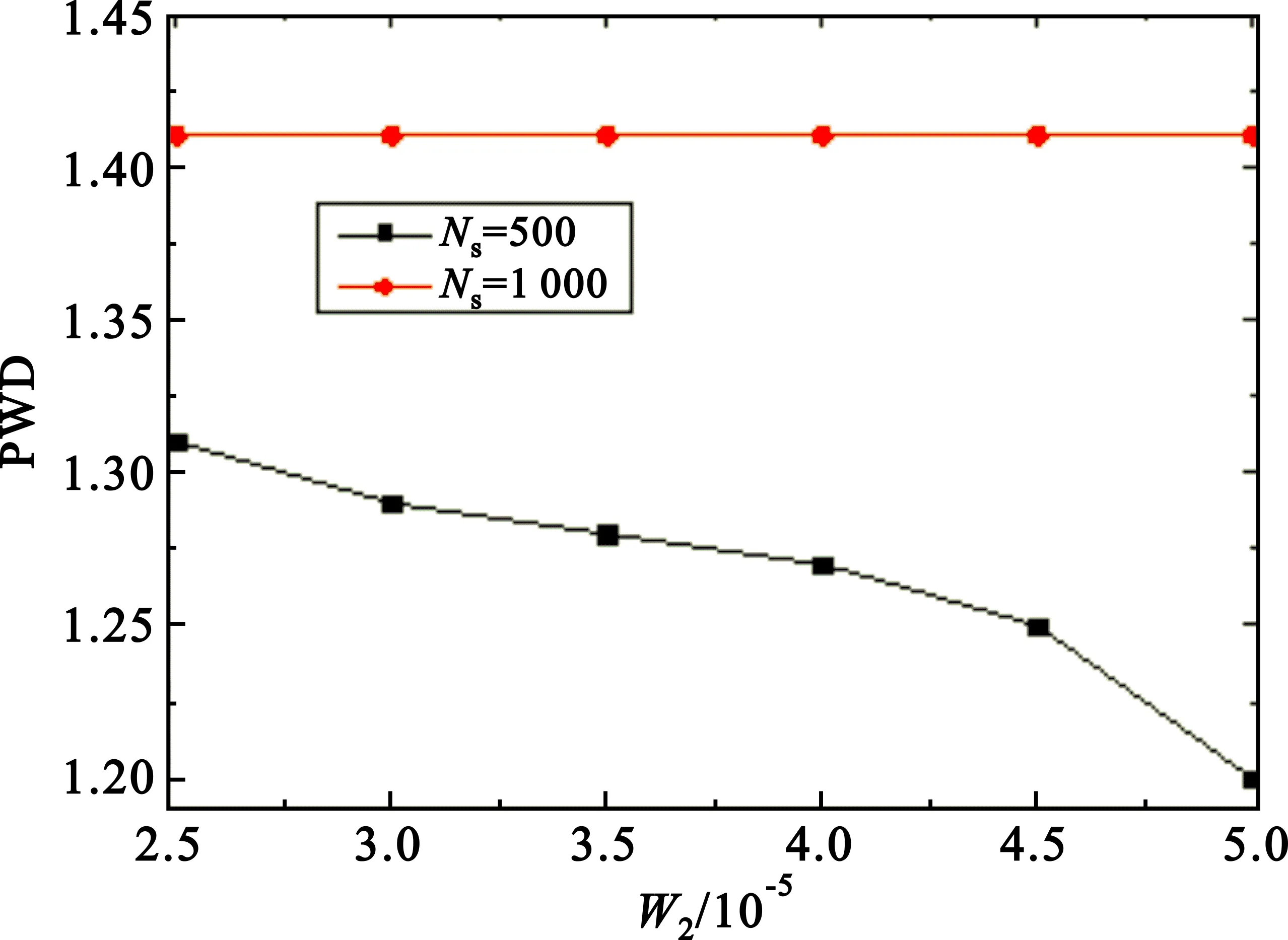
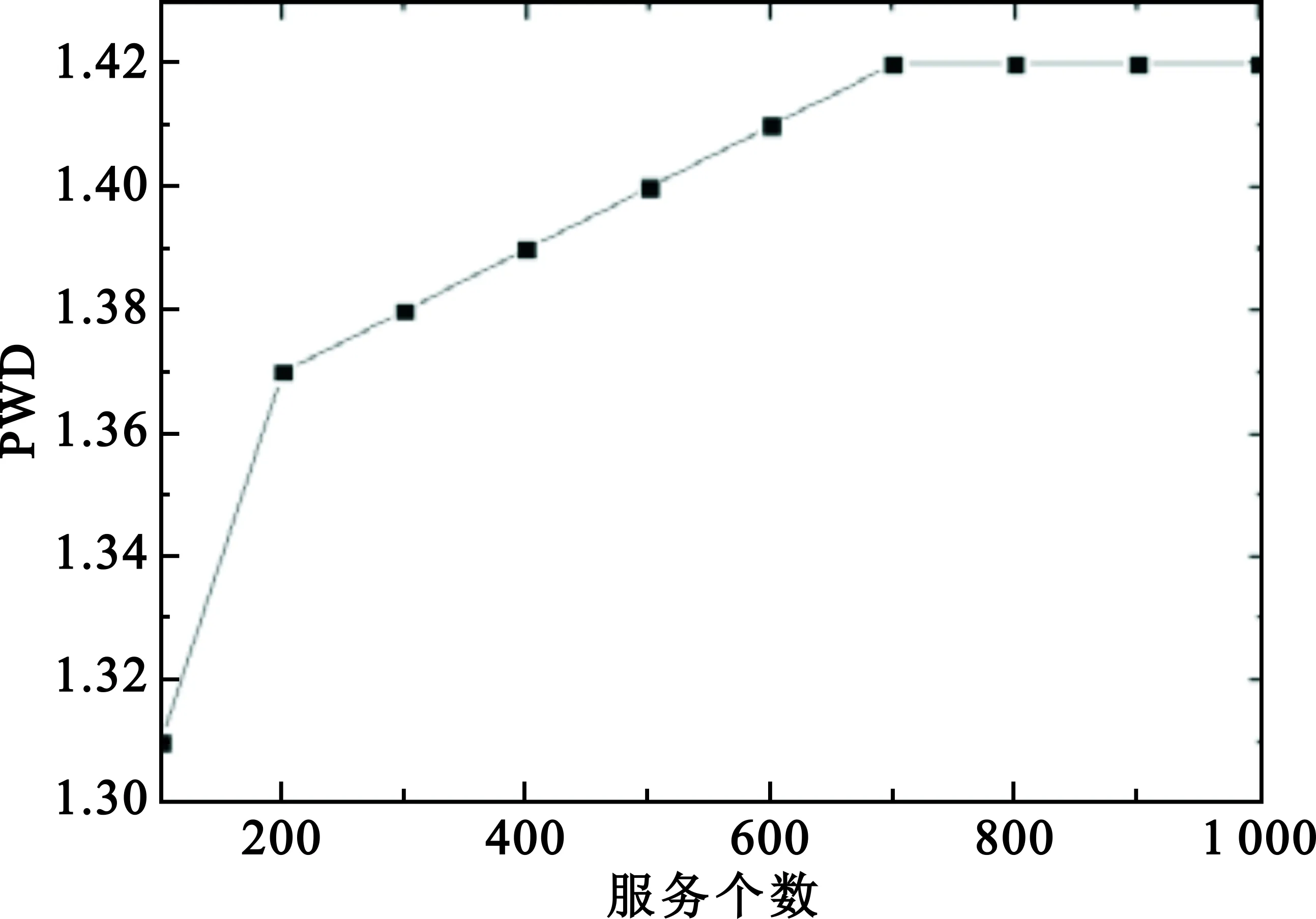
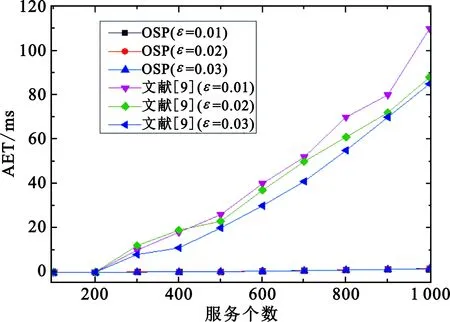
1 To each vertexυ∈Sh,pruneυand its connected edges ifcυ 2 To eache∈EinG(V,E),compute the new weights 3 forδk=0 toΔ,2≤k≤Kdo 4dυ[δ2,…,δK]←∞; 5pυ[δ2,…,δK]←NULL,∀υ∈V 6ds[δ2,…,δK]←0; 7 end for 8 for all (δ2,…,δK)∈{0,1,…,Δ}K-1in increasing lexicographic order do 10 ifdυ[δ2,…,δK]>du[λ2,…,λK]+ω1(u,υ)then 11dυ[δ2,…,δK]←du[λ2,…,λK]+ω1(u,υ) 12pυ[δ2,…,δK]←u 13 end if 14 ifdυ[δ2,…,δK]>dυ[δ2,…,δj-1,…,δK] then 15dυ[δ2,…,δK]←dυ[δ2,…,δj-1,…,δK]; 16pυ[δ2,…,δK]←pυ[δ2,…,δj-1,…,δK],2≤j≤K; 17 end if 18 end for 19 end for 20 ifdt[δ2,…,δK]≤Dthen 21 Find a source-destination pathps.t.ω1(p)≤Dandωk(p)≤δk,2≤k≤K; 22 end if 23 ifωk(p)≤Wk,2≤k≤Kthen 24 return pathp; 25 end if 26 return No feasible path,EXIT. OSP算法主要由以下四个具体步骤构成: Step1(第1行),根据节点约束删减拓扑结构。在服务网络中,cυ Step2(第2行),计算每条边的新权重,设置参数Δ。此时,原始服务网络图就被直接转化成一个更简单的图,达到方便求解QoS感知的服务组合问题可行解的目的。 Step3(第3~19行),初始化(K-1)维数组,运行动态规划过程,搜索服务入口节点s到服务出口节点t之间的路径。 Step3.1 数组dυ[δ2,…,δK]记录从源节点s到任一中间节点υ的路径p第一维参数最小权重(ω1)。此外,该路径p满足ωk(p)≤δk,2≤k≤K。 Step3.2 数组pυ[δ2,…,δK]记录路径p上节点υ的前驱节点。该路径p满足ω1(p)=dυ[δ2,…,δK],且ωk(p)≤δk,2≤k≤K。 Step3.3(第10~13行),当u-υ为图中一条边时,则从节点s到节点υ的第一维最小权重路径p一定经过某些中间节点u,因此本文所提出的OSP算法通过搜索所有可能中间节点u与节点υ之间的边来获得最小的第一维路径权重dυ[δ2,…,δK]。 Step3.4(第14~17行),如果当前记录的第一维路径权重dυ[δ2,…,δK]大于之前的记录值dυ[δ2,…,δj-1,…,δK],则继承以前第一维最小路径权重,即dυ[δ2,…,δK]←dυ[δ2,…,δj-1,…,δK]。这一思路来源于文献[9]中ADAPT算法的思路,可以获得更优的可行解。对于文献[10]中PseudoMCPP算法未能考虑该情形,搜索的最优路径p满足ω1(p)≤D且ωk(p)≤c,2≤k≤K,其中c为正整数,c≤C。结合文献[9-10]的ADAPT算法和PseudoMCPP算法的优点,OSP算法利用路径跳数构建搜索空间,在搜索最优解的过程中不断地继承已知结果,最终获得的最优路径p满足ω1(p)≤D,且ωk(p)≤δk,2≤k≤K,其中δk≤c。因此,对比ADAPT算法和PseudoMCPP算法,本文所提出的OSP算法具有更好的性能,能够快速有效地获得满足用户需求的网络服务组合方案。 Step4(第20~26行),查找Step 3计算结果所获得的路径是否可行,是否满足用户所提约束条件。如果路径P满足ωk(p)≤Wk,2≤k≤K,则算法返回可行路径p;否则返回无可行路径提示,程序终止。 证毕。 证明:对于最优路径popt,有ωk(popt)≤ηopt·Wk,2≤k≤K,即 (9) (10) 由dυ[δ2,…,δK]的定义和动态规划的过程可知, (11) 因此可得 (12) (13) 因为路径p有H-1跳,因此 (14) 即 ωk(p)≤(1+ρ)·η·Wk。 (15) 证毕。 仿真采用两组有向无环图作为数据集。 第一组数据集包括10个有向无环服务网络,服务数规模为100~1 000,其中每个服务网络有3个服务类(H=3),服务数之间的每条有向边有两个QoS参数,即K=2。第一个QoS参数在(2,10)范围内随机取值,第二个QoS参数在(10-8,10-5)范围内随机取值。 第二组数据集包括5个有向无环服务网络,服务数规模为20~100,其中每个服务网络也有3个服务类(H=3),服务数之间的每条有向边有三个QoS参数,即K=3。第一个QoS参数在(2,10)范围内随机取值,第二个QoS参数在(10-8,10-5)范围内随机取值,第三个QoS参数在(0,0.01)范围内随机取值。 为了评价OSP的性能有效性,本文采用平均执行时间(Average Execution Time,AET)和路径权重距离(Path Weight Distance,PWD)两个评价指标来反映算法求解时间和求解质量,以达到测试算法综合性能的目的。 AET主要是用来评估算法在网络延时方面的指标,当网络用户花费的组合路径所需延时越小,则求解时间的性能越好。PWD主要是用来评估不同运行代数下所得到的服务组合路径权重与网络用户路径约束之间的距离,则有 (16) 对于终端用户来讲,这个评价指标反映了算法所获得服务组合路径的QoS保障水平。显然,PWD值越大,算法所获得服务组合路径的质量越好。 根据前面的分析,本文将近似度参数ε引入OSP算法中。测试中将分别设定不同的ε值来分析其对QoS的影响,ε取值分别为0.01、0.02、0.03。对于用户端到端QoS请求,假设W1=50,W2∈[2.5×10-5,5×10-5],以保证算法可以在所有服务网络中找到一条可行的服务组合。分别在ε不同取值条件下,将算法运行1 000次迭代,取20次运行结果的并集,将得到服务组合路径的平均时间值。图3给出了OSP算法在服务数规模为[100,1 000]时获得满足用户需求的服务组合路径所需平均执行时间。当服务数规模增加时,AET值增加,即在更大规模服务网络中需要花费更多时间来寻找相同路径的趋势。随着参数ε值的减少,搜索路径的时间花费AET值增大。这主要是由于算法参数ε取值越小,路径搜索空间越大。因此,参数ε反映的是算法的近似度。ε取值越小,近似度越高,算法的搜索空间就越大,显然算法就需要花费更多的时间查找满足用户需求的服务组合路径。 图3 不同服务数AET值 图4显示了随着ε取值的不同,算法的AET值变化趋势。对于一个给定的ε取值[0.01,0.03],在服务数[100,1 000]的范围内,OSP算法的搜索空间依赖于服务组合路径的跳数,其路径跳数值小并且可以预先获得,容易快速有效地构建搜索空间。OSP算法能较快找到服务组合路径,算法的平均执行时间AET值较小,尤其是在更大的服务数下表现较为突出。 图4 ε取值[0.01,0.03]下OSP算法的AET值 图5(a)为在服务数为500和1 000、不同ε取值的情况下AET的值。从图中可以看出,不同的ε取值,OSP算法可以较快地满足用户QoS需求的服务组合路径。此外,随着算法ε取值的增大,OSF算法也表现出更加稳定的AET性能。也就是说,当满足用户需求的服务组合路径存在于搜索空间中的某一特定位置时,AET值较为稳定。这是因为,OSP算法在服务组合路径跳数构建搜索空间,参数ε起着微调该搜索空间的作用。图5(b)为在服务数为500和1 000、不同约束值(W2)取值的情况下AET的值。实验结果表明,在不同约束情况下,OSP算法的AET值并不受用户约束的影响,随着用户约束值变大,算法中的AET值趋势稳定,始终保持在一个稳定的状态。 (a)不同ε值下的AET取值 图6给出了OSP算法在不同约束值(W2)情况下的PWD值。随着用户约束逐步放松,OSP算法搜索的路径距离将减小,即PWD值减小。也就是说,如果用户需求宽松,OSP算法将找到质量更粗糙的路径,只需满足用户的要求即可。由此可知,当服务数增大时,OSP算法可以找到更好质量的服务组合路径。 图6 服务数为500和1 000的W2的PWD值 图7给出了OSP算法在不同网络服务数下PWD值。从图中可以看出,随着网络服务数的增加,OSP算法可以找到更好质量的服务组合路径。这是因为在某一个更大规模的服务网络中有着更优的服务组合选择路径。这表明OSP算法可以根据用户需求,在不同服务网络数下稳定、可靠地找到满足端对端的QoS约束服务组合路径。 图7 不同服务数PWD值 由于云计算所持有的服务形态、服务模式和服务规模,以及云服务和网络服务的QoS参数特性,ADAPT算法优势在于在搜索最优解的过程中继承已知结果。为了证验ADAPT和OSP两种算法的性能,我们将文献[9]的ADAPT算法与OSP算法进行对比。图8(a)给出了两个算法在不同网络服务数、相用ε取值下的AET对比值。测试结果表明,对于一个给定的ε取值,OSP算法可以更快地找到与运行ADAPT算法一样的服务组合路径,即OSP算法的AET值更小。随着服务数的增大,它的优势更为明显。而ADAPT算法采用的算法由于逐步压缩路径上下界,过程较为缓慢,并且其最终所构建的搜索空间大于依靠跳数构建的搜索空间。因此,与ADAPT算法对比,OSP算法的AET性能方面优势更为明显。 图8(b)、8(c)分别给出了两个算法在相同服务数(500和1 000)、不同ε取值下和不同约束值W2时的AET对比值。对于不同的ε和W2取值,OSP算法均优于ADAPT算法,即可更快找到满足用户QoS需求的服务组合路径。随着算法参数ε取值的增大,OSP算法的AET值较为平稳,而ADAPT算法的AET值逐渐变小。这说明,当满足用户需求的服务组合路径存在于搜索空间中的某一特定位置时,ADAPT算法对参数ε取值敏感,并受W2约束,而OSP算法稳定性强。 (a)不同服务数下的AET对比值 本文针对网络服务组合的特点和用户个性化的QOS需求,分析和定义了多融合网络场景下的网络感知服务组合模型,提出了一种基于最优路径选择的服务组合算法,大大提升了网络服务质量。实验结果表明,该算法在求解时间和质量两个方面都表现出了良好的性能,而且能动态适应用户复杂的需求。同时,OSP算法优于ADAPT算法。在实际应用中,许多APP服营商(比如掌上高铁、微信等)在对相关服务进行整合关联时,会对相关应用程序进行接口对接,以达到服务的快速关联,可大大提升QoS的效益。随着技术的不断推进,相信本方法将满足云环境下QoS关联的服务组合要求。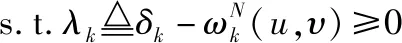
2.2 算法分析
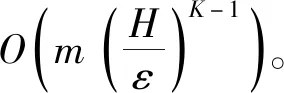
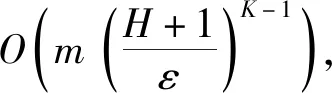
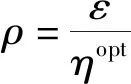
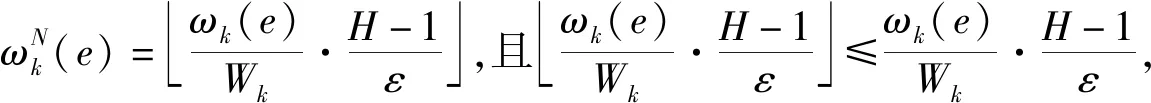
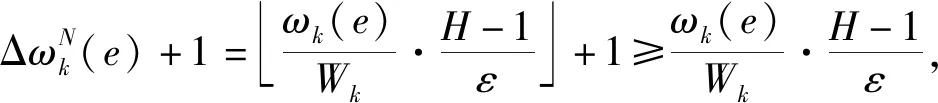
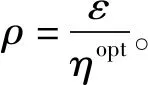
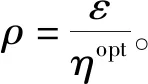
3 仿真测试与分析
3.1 测试准备
3.2 测试指标
3.3 测试结果
3.4 与ADAPT的对比
4 结 论

