一种采用改良基-26算法的低复杂度高吞吐量FFT处理器设计*
于 建
(河北民族师范学院 物理与电子工程学院,河北 承德 067000)
0 引 言
随着多媒体应用在短距离无线传输方面日益增长的需求,多年来针对60 GHz毫米波无线个人局域网(Wireless Personal Area Network,WPAN)通信技术的研究受到了广泛的关注。IEEE802.15.3c任务组为60 GHz千兆比特WPAN系统制定了相应标准,要求其提供超过2 Gb/s数据传输速率[1]。
在高速率WPAN系统的物理层设计中采用了正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)调制技术,快速傅里叶变换(Fast Fourier Transform,FFT)处理器是OFDM系统中硬件复杂度最高的模块。在基于OFDM调制技术的高速率WPAN系统中,一个OFDM符号一般由512个子载波组成,OFDM符号持续时间为222.22 ns。这就意味着要求所设计的FFT处理器至少提供2.304 Gsample/s的高数据吞吐量[2]。实际上为了获得更好的带宽效率,设计上FFT的点数一般都会超过512,这样势必导致需要更长的字长来维持一定的信号量化噪声比(Signal to Quantization Noise Ratio,SQNR),大幅增加了所需的硬件成本[3]。在实现高吞吐量的FFT处理器设计方面,许多研究都采用了多路径负反馈流水线架构(Multi-path Delay Feedback,MDF)[1-5],其原理就是根据路径数复制单路径上的FFT处理器运算模块,但硬件成本会随着路径数的增加而成倍的增长。因此,许多学者提出了不同的FFT算法用于降低单路径上FFT运算模块的硬件复杂度,其中基-2k算法最为著名[6]。基-2k算法不论k值的大小,都拥有与基-2算法一样简单的蝶形架构,但不同的k值会导致其具有不同的旋转因子复数乘法结构[7],因此需要根据旋转因子复数乘法的复杂度选择最优k值的基-2k算法用于优化FFT处理器的设计。
为了有效降低硬件实现复杂度并保证高速率、高精度的数据传输,本文提出了一种基于改良基-26算法2 048点8路MDF FFT处理器设计方案,能够提供2.6 Gsample/s高数据吞吐量并有效控制硬件成本,同时SQNR达到了36 dB。
1 算法选择
N点离散傅里叶变换(Discrete Fourier Transform,DFT)定义如式(1)所示:
(1)
式中:WN为旋转因子,其指数k和n分别代表频域索引与时域索引。直接实现式(1)中的DFT会消耗大量的硬件成本和计算时间,因此众多FFT算法被提出用于减少DFT的计算时间与硬件资源消耗。由于基-2k算法不但拥有与基-2算法一样简单的蝶形单元架构,同时还能减少旋转因子复数乘法的运算复杂度,因此常被用于FFT处理器的硬件实现上。本文提出了一种新型改良基-26算法用于2 048点FFT处理器的设计。
1.1 改良基-26 FFT算法
所提出的改良基-26算法采用7维度线性索引图进行表述,如式(2)和式(3)所示:
(2)
k=k1+2k2+4k3+8k4+16k5+32k6+64k7。
(3)

改良基-26算法可分为两种方式进行表达,方式1的因子计算公式如式(4)所示:
X(k1+2k2+4k3+8k4+16k5+32k6+64k7)=
(4)
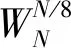

(5)
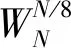
X(k1+2k2+4k3+8k4+16k5+32k6+64k7)=
(6)
(7)
1.2 算法评估
由于负责旋转因子复数乘法运算的乘法器在FFT处理器中占用主要的硬件资源,因此选择旋转因子复杂度低的基-2k算法是十分必要的。表1所示为不同k值2 048点基-2kFFT算法旋转因子复数乘法运算分布。由表1可知,2 048点基-2kFFT算法一共包含了10个旋转因子复数乘法运算,其中‘-j’运算为简单运算,只需将复数序列的实部与虚部的位置进行交换,再对虚部求反即可。由于旋转因子W8、W16、W32和W64进行复数乘法运算所需的常数值个数少,因此为了节约硬件成本,在实现它们的复数乘法运算采用了正则有符号数(Canonical Signed Digit,CSD)常数乘法器[8],而对于旋转因子W128、W256和W2048来说,其所需常数值过多,已不适合利用CSD常数乘法器,因此采用常用的布斯乘法器进行复数乘法运算。仔细观察表1,本文提出的改良基-26算法不论是方式1还是方式2与其他算法相比,在减少旋转因子计算复杂度方面并无明显优势。考虑到改良基-26算法每6个阶段为一个旋转因子复数乘法循环周期,比较方式1和方式2的第一个循环周期的旋转因子(前6个阶段),除了同样的旋转因子W2048和W64,方式1中剩下W16,方式2中剩下W8和W32,明显方式1较方式2具有更简单的旋转因子;同样,在后续的4个阶段中,方式2的旋转因子W8和W32对比方式1的旋转因子W16和W64更加简单。因此将方式1的前6个阶段(表1中红色矩形圈住的部分)与方式2的后4个阶段(表1中蓝色矩形圈住的部分)相结合,形成混合改良基-26算法,对比其他k值的基-2k算法拥有更简单的旋转因子。

表1 2 048点基-2k算法旋转因子运算分布
表2所示为8路径2 048点不同k值的基-2kMDF FFT架构硬件复杂度比较,为了更直观地评估,对于复数乘法器的逻辑单元(Logic Element,LE)使用量进行了归一化处理,用NLE表示,布斯乘法器所消耗的LE设定为1,那么完成旋转因子W8、W16、W32和W64的CSD常数乘法器所消耗的LE分别为0.09、0.18、0.33和0.59。由表2可知,相较于其他k值的基-2k算法,新型改良混合基-26算法拥有最低的逻辑单元消耗量和最小的ROM存储空间(本文第2节将给出详细的ROM空间减少方案),因此新型混合改良基-26算法在2 048点FFT处理器设计上更具优势。

表2 8路径2 048点不同k值基-2k MDF FFT架构设计硬件复杂度比较
2 设计方案
图1所示为混合改良基-26算法8路径2 048点FFT处理器整体结构图。由图1可知,本文所设计的FFT处理器由基本的蝶形单元、布斯乘法器、ROM、CSD常数乘法器以及控制逻辑所组成,其中左边的模块1用于完成混合改良基-26算法方式1前6个阶段的运算,右边的模块2用于完成混合改良基-26算法方式2后4个阶段的运算。

图1 基于混合改良基-26算法的8路径2 048点FFT处理器结构图
2.1 蝶形单元
蝶形单元是FFT处理器中最基本的运算单元,主要用于复数序列的加法与减法。蝶形单元分为BFI型与BFII型,与前者不同的是后者需要进行额外的‘-j’运算[9]。蝶形单元的具体运算过程如下:
输入数据序列按照顺序储存到先进先出寄存器中,直到第N/2个数据(N为FFT点数),接下来的输入数据与先前存放在寄存器中的数据依次进行复数加减法运算。蝶形单元所进行的复数加法运算直接作为下一个阶段的输入数据,而减法运算结果存入下一阶段的先进先出寄存器中。
2.2 布斯乘法器与ROM
由于布斯乘法器能将乘法的部分积减少一半,非常适合高速FFT处理器的复数乘法运算。同时,考虑到量化误差对整个FFT处理器SQNR的影响,本文的设计方案采用了文献[10]的布斯乘法器误差补偿方案用于减少量化误差。布斯乘法器在针对旋转因子进行复数乘法运算时,需要ROM对旋转因子的系数进行存储。本文采用了一种减少ROM存储空间的方法[11],能够将存储旋转因子W2048系数的空间减少为原来的一半。具体方法如下:
ROM存储空间的大小依赖于旋转因子指数的最大值、最小值以及指数最小间隔步长,而且ROM存储空间大小为2的整次幂。例如,如果旋转因子WN的指数i(i=nk)最小值为0,最大值为12,而指数之间的间隔为1,那么至少需要16 b的存储空间(为了方便计算,这里不考虑旋转因子序列的字长),但如果指数最大值与最小值不变,最小间隔步长变为2,那么根据旋转因子的可约性,指数i的取值范围缩小为原来的一半,此时只需8 b的存储空间。由于本文的设计需要利用布斯乘法器来处理旋转因子W2048的复数乘法运算,因此为了确定所需ROM存储空间大小,基于Matlab对2 048点不同k值的基-2k算法进行了建模。
通过下面的代码可获得旋转因子W2048所需的相应指数:
exp=[0:N/2k];B=de2bi([0:2k],'left-msb');
C=fliplr(B);D=bi2de(C,'left-msb');
tw_r2k=exp.*D;
%其中N为FFT点数;k为基-2k算法的指数;%
表3所示为不同k值的基-2k算法针对旋转因子W2048所需ROM存储空间的比较。

表3 不同基-2k算法所需ROM存储空间比较

图模块结构图
2.3 CSD常数乘法器
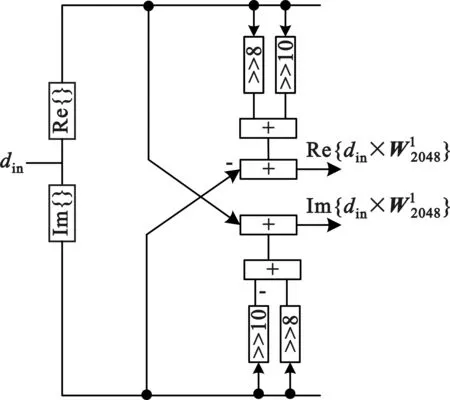
本文提出的设计方案需要4种不同的CSD常数乘法器来分别完成旋转因子W8、W16、W32和W64的复数乘法运算,表4给出了上述CSD常数乘法器所需的15个常数值以及其CSD表示。

表4 15组常数值CSD表示
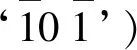

图3 CSD常数乘法器结构图(W8、W16、W32和W64)
3 不同方案FFT处理器性能比较
在FFT处理器的硬件实现之前,基于Matlab对序列字长选择以及量化误差进行了相关的评估。本文的设计采用定点字长方案[12],图4所示为基-2k算法在不同字长时计算2 048点FFT的SQNR表现。由图4可知,不论基-2k算法的k值如何,当序列内部字长增加到16 b时,SQNR达到了36 dB,继续增加字长,SQNR并无显著提升,因此本文设计选择16位内部字长。

图4 基-2k算法SQNR比较
基于QUARTUS PRIME平台对所提出的2 048点FFT处理器进行了实现与仿真,使用Verilog HDL语言对设计进行建模,器件选择CYCLONE 10LP家族的10CL120ZF780I8G。表5所示为本文的方案对比其他已存在方案在面向WPAN应用所设计的FFT处理器性能仿真结果比较。为了更加直观地评估硬件成本的消耗,将逻辑单元使用量以及记忆体单元使用量(Memory Bit,MB)进行了标准化处理,本文方案所消耗的LE与MB均设定为1。由表5可知,对比已有的设计方案,本文方案至少能够节约23%LE以及12%MB,同时本文所设计的FFT处理器有着更好的SQNR表现,最高工作频率达到了320 MHz,此时数据吞吐量为2.6 Gsample/s。利用QUARTUS PRIME平台的Power Analyzer进行功耗分析,本文所设计的FFT处理器动态功耗最低,仅为33.8 mW。

表5 不同方案FFT处理器性能比较
图5所示为MODELSIM得到的RTL级仿真结果幅度值与Matlab计算结果幅度值的比较(输入序列的实部和虚部都设定为1~2 048)。图5中的缩略图截取了不同FFT点数位置上的计算结果,由四个缩略图可知,RTL级仿真结果与Matlab计算结果全部吻合,验证了设计的有效性。

图5 RTL级仿真结果与Matlab计算结果比较
4 结 论
本文设计了一种基于新型改良基-26算法的8路径MDF架构2 048点FFT处理器,能够为WPAN应用提供高达2.6 Gsample/s的数据吞吐量。提出的改良基-26算法降低了旋转因子复数乘法运算的复杂度,为了降低硬件资源消耗,采用CSD常数乘法器替代传统布斯乘法器完成了除旋转因子W2048的所有复数乘法运算,对比已有的方案,至少能够节约23%LE与12%MB。同时,在16位内部定点字长的条件下SQNR达到了36 dB,动态功耗仅为33.8 mW。另外,采用了一种减少存储旋转因子W2048系数ROM空间的方法,使得为布斯乘法器提供旋转因子系数的ROM存储空间减少为原来的一半。因此,本文所提出的方案在面向WPAN应用的高吞吐量、低复杂FFT处理器设计上具有较大的优势。

