面向智能反射面辅助通信的深度学习信号检测*

霍浩淼，许威,2**，陈栋

（1.东南大学信息科学与工程学院，江苏 南京 210096；2.紫金山实验室，江苏 南京 211111；3.小米科技有限责任公司，北京 100085）

0 引言

大规模毫米波多输入多输出（MIMO,Multi-Input Multi-Output）相较于传统的MIMO 技术的收发天线数较大，这带来了性能优势的同时信号检测的复杂度也随之增大。传统的检测方案中，性能最优的最大似然（ML,Maximum Likelihood）信号检测方法计算复杂度极高，随着传送天线数以及调制维度的增加，该算法的复杂度呈指数增加。复杂度低的一些线性检测算法如最小均方误差（MMSE,Minimum Mean Squared Error）检测算法，受复杂信道环境、信道估计误差及大量非线性因素影响，性能往往比ML 差3 dB 以上[1]。

深度学习（DL,Deep Learning）利用深度神经网络（DNN,Deep Neural Networks）已经成功地应用于通信中的各种场景[2]。深度学习以其独特的训练原理，不需要了解具体的工作机制，只需要合适的网络和足够的训练数据就能解决问题，在处理非线性问题上已经显示出巨大的潜力。文献[3] 提出了一种被采用较多的检测网络（DetNet,Detection Network），它的结构可以看作是一个展开的递归神经网络，性能优于一般的线性检测算法，但DetNet 网络设计中的辅助输入输出结构增加了检测的复杂度。

智能反射面（IRS,Intelligent Reflecting Surface）是一种面向后5G 的新型通信方法[4]。它是由大量可重构无源元件组成的平面阵列，通过智能控制器，每个元件都能够独立地在入射信号上产生一定大小的相移，改变反射信号的传播。IRS 通过将来自发射端的信号反射到接收端来协助通信，因为引入了智能反射面，IRS 辅助通信的检测问题参数维度更大，复杂度也更高。

考虑到IRS 辅助通信系统中应用DL 进行信号检测的潜力，本文根据IRS 信道特点和梯度下降更新思想，设计了一种应用于IRS 辅助通信的低复杂度深度检测网络，并给出了智能反射面辅助通信深度检测网络的仿真结果，最后对复杂度和误码率性能进行了对比。

1 系统模型

图1 为基站和终端借助智能反射面进行辅助通信的系统，IRS 通过将来自基站S的信号反射到终端D协助通信。其中，基站S天线数为M，终端D天线数为N，IRS 由K个被动的反射元件组成，这些元件可以使用面向通信的软件进行控制并重新配置。

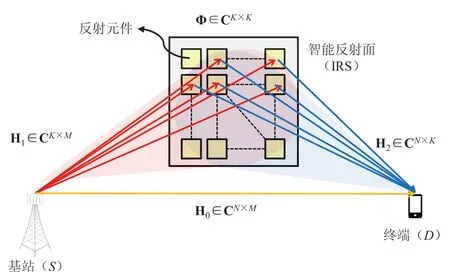
图1 IRS辅助MIMO通信系统模型

终端接收到的信号为：

2 智能反射面辅助通信深度检测网络

2.1 最大似然检测算法

ML 检测算法是性能最优的信号检测算法，其判决准则为选择使得信道转移概率最大的向量ˆx 作为发射符号向量的估计值，即令，在所有可能的发射集合中找出满足的发送集合。其中，Ω 表示所有发射符号向量的集合。

MIMO 信道的信道转移概率是一个多维高斯分布，求得最大似然检测的解为：

2.2 梯度下降思想迭代检测算法

采用深度学习解决信号检测问题，可以描述为设计恰当的检测网络结构，训练适合的网络参数，使得检测网络的输出与实际传输信号的损失函数最小，以代替ML等传统检测器的作用。因此，智能反射面辅助通信检测问题就转化为了求解下述优化问题：

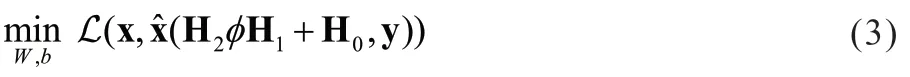
其中，W表示网络权重，b表示网络偏置，表示检测网络输出的发射信号，L表示网络损失函数。

在IRS-MIMO 检测问题中采用梯度下降算法更新x的近似值为：

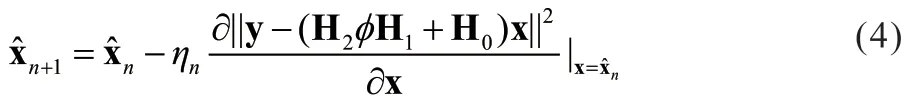
将式(4)展开，得到：

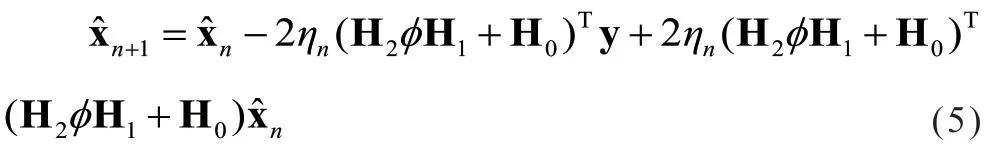
对于一次梯度下降迭代更新过程，信道矩阵通过信道估计得到，式子右边的部分均为已知量，根据梯度下降更新算法的思想进行检测网络的结构设计。

2.3 智能反射面辅助通信深度学习检测网络结构设计

根据式(5)，本文提出了一种智能反射面辅助通信深度学习检测网络，将式中的已知量作为网络设计的参数，根据展开式设计网络的输入输出形式。网络结构如图2 所示，由L个结构相似的单元级联组成，每个检测网络单元的输入为(H2φH1+H0)Ty、(H2φH1+H0)T(H2φH1+H0)和，输出为，其中每个单元的输出作为下一个单元的输入，也可以作为整个网络的输出。随着网络单元数的增加，检测网络的输出更接近于发送信号。

图2 智能反射面辅助通信深度检测网络结构

每个单元由三层全连接层和一个短路直连结构组成：第一层为3M*1 的输入层，对应式(5) 中的输入参数，M表示基站发射天线数，串联连接所有输入向量，并转换成一维向量，然后输出通过一个具有大量节点的全连接网络，采用sigmod 函数作为激活函数，输出和一个关于的短路直连一起作为下一层的输入。通过引入短路直连结构，可以强化部分输入的作用，充分挖掘复杂信道的非线性关系。第二层为4M*1 的隐藏层，采用tanh 函数作为激活函数。第三层为M*1 的输出层，每个单元的输出均可以作为下一个单元的输入或整个网络的输出。

每个网络单元在检测网络中具有不同的重要性，研究证明靠前的网络单元在网络中的作用大于靠后的单元，因此本文在检测网络中引入权重缩放向量系数，将单调的非递增系数应用于单元权重系数，按照重要性递减方式选择单元权重，忽略不重要的网络单元，降低了训练检测器的计算复杂度。网络选取的权重缩放向量系数为半指数函数：

其中，L表示网络的单元数。

为了降低网络训练过程的复杂度，设计了不包含矩阵求逆过程的网络损失函数为：

根据设计的智能反射面辅助通信深度检测网络，本文提出的智能反射面辅助通信深度学习信号检测算法如下：

输入：y、H0、H1、H2、φ

参数：W、b、β

步骤：

（1）根据信道估计获得矩阵数据，组合y、H0、H1、H2和φ，获得输入向量；

（2）训练数据输入检测网络，计算损失函数；

（3）采用Adam 优化算法和端到端学习方式，优化深度检测网络的参数，使得损失函数最小；

（4）重复步骤（2）、（3）直到收敛；

3 仿真结果与复杂度分析

为了验证提出的检测网络的有效性，本节仿真了智能反射面辅助通信系统深度学习检测网络的误码率性能曲线，并与经典检测算法的性能进行比较。仿真的系统模型调制方式为QPSK，基站天线数M为8，终端天线数N为2，深度检测网络单元数为90，系统样本数为10 000，其中80%用于训练集、10%用于测试集、10%用于验证集，网络采用变化的学习率，初始学习率为0.001，衰变因子和衰变步长分别为0.97、1 000。

图3、图4 和图5 展示了具有不同大小的IRS 阵列的通信系统在7～15 dB 信噪比（SNR,Signal-to-Noise Ratios）下的误码率性能曲线。

图3 展示了IRS 单元数K=16 时的误码率性能曲线。可以看出，智能反射面辅助通信深度学习检测网络具有远优于MMSE 等线性检测算法的误码率性能。在SNR 为11 dB 时，智能反射面辅助通信深度学习检测网络相较于MMSE 检测方法有接近2 dB 的性能增益，与ML 最优检测算法的差距在0.8 dB 左右。

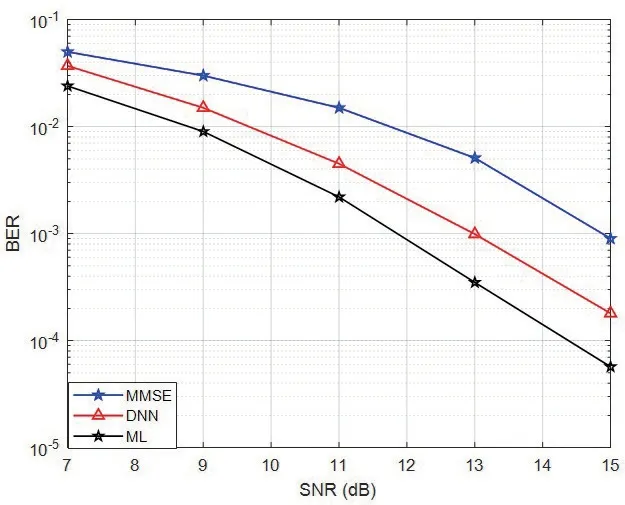
图3 K=16时各检测算法误码率曲线

图4 展示了IRS 单元数K=36 时的误码率性能曲线。可以看出，智能反射面辅助通信深度学习检测网络仍然具有优越的误码率性能。在SNR 为11 dB 时，智能反射面辅助通信深度学习检测网络相较于MMSE 检测方法有接近2.2 dB 的性能增益，与ML 最优检测算法的差距在0.6 dB 左右。

图4 K=36时各检测算法误码率曲线

图5 展示了IRS 单元数K=64 时的误码率性能曲线。可以看出，在配备更大IRS 阵列的通信系统中，智能反射面辅助通信深度学习检测网络仍然具有优越的误码率性能。在SNR 为11 dB 时，智能反射面辅助通信深度学习检测网络相较于MMSE 检测方法有接近2.2 dB 的性能增益。

图5 K=64时各检测算法误码率曲线

表1 对比了深度学习检测网络与一些经典检测方法的计算复杂度，其中Q表示调制阶数。智能反射面辅助通信深度学习检测网络的计算量可以用浮点运算数表示，计算为(2×3M-1)×M×L=6M2L-ML，因此深度学习检测网络的复杂度量级为O(M2L)。从表1 中可以看出，智能反射面辅助通信深度学习检测网络具有和线性检测算法同一量级的复杂度，远低于ML 最优检测算法的复杂度。

表1 各检测算法复杂度对比

4 结束语

本文根据检测问题中梯度下降更新算法的展开式，设计了一种低复杂度的面向智能反射面辅助通信的深度学习检测网络。该网络采用多个具有相似结构的单元级联，在单元中引入短路直连结构加强部分输入的影响，并通过单元权重系数对不同单元的重要性进行调节。仿真结果表明，智能反射面辅助通信深度学习检测网络具有和线性检测算法相当的计算复杂度，远低于最大似然检测，并且具有优于MMSE 等线性检测算法的误码率性能。在未来的工作中，可考虑将此检测网络推广到更大规模智能反射阵列和高阶调制方案上。