高耸烟囱在高温作用下的风振响应分析
吴松涛,范存新
(苏州科技大学土木工程学院,江苏 苏州 215011)
0 引言
烟囱是工业建筑中的一种特种结构,随着现代工业的发展,烟囱的高度也在逐步增加。在钢铁厂、火力发电厂等工厂内,一般都建有几十米到几百米不等的烟囱。其结构形式一般为单筒式烟囱、套筒烟囱或多管烟囱,且具有结构的高宽比较大的特点,是一种典型柔性高耸结构,受风荷载的影响非常显著。在实际生产过程中,工业排放的烟气往往都是高温气体,烟气的温度对烟囱的筒体本身产生一定的影响,况且烟囱的筒体在使用过程中常年处于高温作用的状态,一方面高温烟气会渗透到筒壁内部,另一方面随着烟囱的长时间使用以及隔热材料的老化,筒壁完全有可能在高温状态下工作。因此我们对高耸烟囱进行风振响应研究时,应该充分考虑在高温烟气影响下,烟囱筒壁钢筋与混凝土的力学性能发生改变后,会对风振响应的结果造成一定的影响。近年来,国内外学者对烟囱遭受风振破坏和受高温破坏方面的研究已经取得了一定的进展。其中,陈鑫等[1]根据高耸烟囱的特点,建立其质量模型的动力微分方程,通过改进谐波叠加法来模拟风荷载,最后编制程序针对烟囱在顺风向和横风向风振情况下在时域和频域内求解。张玉梅等[2]通过24个不同几何参数的烟囱,用有限元模拟其温度场分布结果,并与试验结果对比分析,确认出一个计算烟囱温度场的简单方法。郑欢[3]探讨了考虑温度影响与不考虑温度影响的烟囱几何非线性地震响应分析,得出温度的影响程度与地震动的频谱特性有关的结论。G.K.Verboom等[4]依据多种规范对13个高耸钢烟囱的横向风振动进行了对比研究。
综上所述,单独考虑风振、高温和地震等因素对烟囱结构影响的研究颇多,而烟囱的结构稳定是受到多种因素共同作用的结果,且多项受力的耦合分析相对复杂,难以收敛,因此本文对高耸烟囱在高温作用下的风振响应分析进行研究,对实际工程具有一定的参考意义。本文以某高耸钢筋混凝土烟囱为研究对象,首先利用ABAQUS软件模拟烟囱工作时的温度场,得出烟囱筒壁的升温曲线,确定其所受的最高温度,然后通过MATLAB软件模拟脉动风速,计算风荷载,再由ABAQUS有限元软件进行动力时程非线性分析,分别得出常温下的风振响应结果和考虑高温作用后的风振响应结果,并进行对比研究。
1 计算模型
1.1 工程概况
本文所研究的烟囱的结构型式为钢筋混凝土单筒烟囱。烟囱标高180 m,筒壁底部内半径8.38 m,外半径8.88 m,顶部内半径3.75 m,外半径3.93 m。烟囱主要由钢筋网、混凝土层和内衬、隔热层三部分组成,其中内外纵筋主材采用HRB335钢,内外箍筋则均为HPB300钢,筒壁采用C35混凝土,隔热层为憎水性水玻璃珍珠岩板,内衬为耐酸陶土砖。
1.2 烟囱有限元模型
基于ABAQUS软件,按照实际模型图纸,采用分离式建模方法,建立了某180 m高的钢筋混凝土单筒烟囱的三维有限元模型。其中钢筋均采用桁架单元进行模拟,筒壁混凝土层和内衬采用均质实体单元模拟;隔热层则采用均质壳单元进行模拟,模型的具体力学参数如表1所示。模型考虑了钢筋混凝土材料的非线性,依据《混凝土结构设计规范》[5]采用弹塑性本构模型。建立的高耸烟囱有限元模型如图1所示。

表1 模型相关参数

图1 烟囱有限元模型
2 温度场分析
2.1 温度场模拟方法
为了得到在高温烟气作用下烟囱内部各点不同时刻的温度变化情况和烟囱筒壁的升温曲线,本文利用ABAQUS软件对烟囱进行热传递分析,得到的温度场结果用以后续计算考虑高温作用后的风振响应。
在烟囱正常启动工作时,多种因素都会影响烟囱筒壁的温度场,例如烟囱自身沿高度有显著的坡度变化,还可能受到高温烟气的流动、腐蚀,以及烟囱外界气温改变、日光辐射、风力等的影响。本文认为烟囱筒壁的温度场分布随时间不断地发生变化,故采用不规则边界条件下的柱坐标三维瞬态导热的温度场模型[6]。
为了简化计算,本文不考虑烟气温度会沿烟囱高度降低的情况,均取烟气的最高温度,因此钢筋混凝土烟囱首先受到假定为恒温的高温烟气作用,然后高温烟气对内衬进行热对流作用,接着内衬对隔热层进行热传导作用,同时隔热材料把热量以热传导的形式传递给钢筋混凝土层,最后烟囱的外表面把热量以热辐射的形式传递给外界大气。其中的热对流作用使用国际标准升温曲线ISO-834来模拟(如图2所示),热传导作用通过在ABAQUS软件中定义如表2、3所示的材料热学参数来模拟[7],热辐射则通过有限元软件自带功能实现。
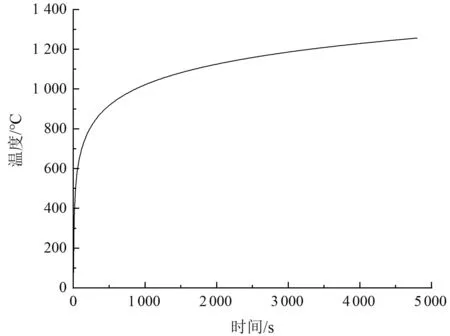
图2 ISO-834标准升温曲线

表2 混凝土的热学性能

表3 钢筋的热学性能
2.2 温度场计算结果
本文使用ABAQUS软件进行烟囱温度场有限元分析,烟囱的环境温度选取为常温25 ℃,烟囱的升温时间为8 h,得到结果如图3~4所示。

图3 烟囱整体截面温度云图(单位:℃)

图4 烟囱顶部筒壁内外表面温度
从图3~4可以发现,烟囱在高温烟气作用下,其截面温度随之升高,整体呈现出由内到外,温度逐渐降低的情况。内衬耐火砖由于直接接触高温烟气作用,因此整体温度最高,珍珠岩板隔热层其次。当热量最终传递到钢筋混凝土筒壁内侧时,最高不超过140 ℃,满足规范[8]中对钢筋混凝土烟囱筒壁最高受热温度不超过150 ℃的要求。烟囱外表面由于和外界空气接触,发生热辐射,因此升温较为缓慢,且最高温度出现在烟囱顶部,最高升至70 ℃左右。可见烟囱的隔热层起到了一定的隔热作用。
3 风与温度耦合作用
3.1 线性滤波法模拟风速
本文通过编写MATLAB程序来模拟脉动风速时程曲线[9-10]。由于烟囱截面为圆形对称结构,因此各风向角对结构风荷载没有影响。该烟囱高180 m,每隔10 m取一个风速模拟点,共计18个点。模拟选用Davenport谱,地貌类别B类,平均风速取30 m/s,时间步长取0.125 s,风速计算时长30 s,得到烟囱18个模拟点处的风速。图5所示为坐标(0,0,180)烟囱顶点处的总风速时程曲线。按公式(1)将风速换算成烟囱各段上的等效节点荷载[11],施加在模型上的x方向。
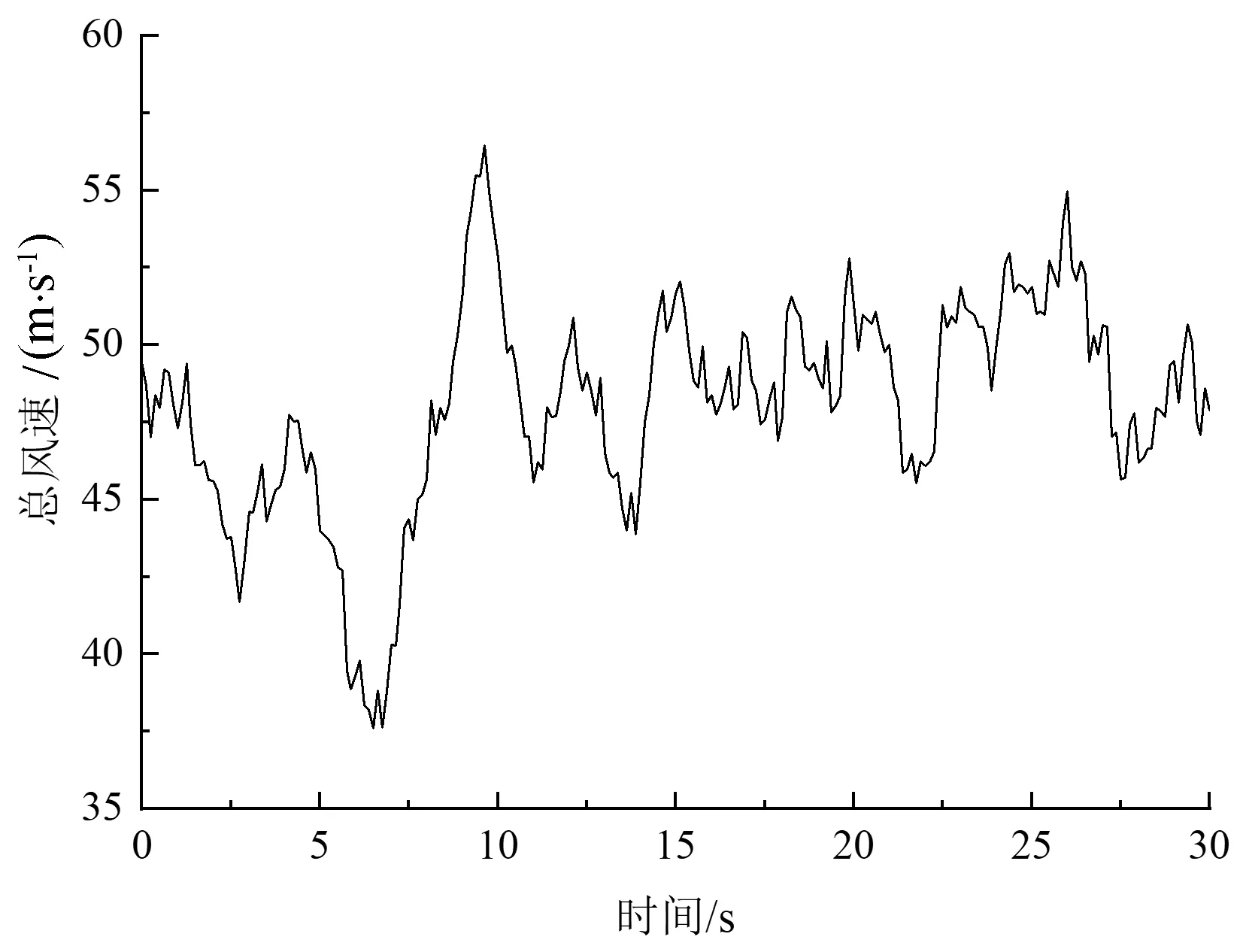
图5 烟囱顶点总风速时程图

(1)
式中:Fi(t)为t时第i段的等效节点荷载;μsi为烟囱第i段的体型系数;μzi为烟囱第i段的风压高度变化系数;Afi为烟囱第i段的投影面积;v为总风速,由平均风与脉动风叠加。
由此可以得到烟囱各段的风荷载值,以烟囱顶点处筒段为例,如图6所示。

图6 烟囱顶点风荷载时程图
3.2 钢筋与混凝土在高温下的力学性能
烟囱受到高温烟气作用后,钢筋混凝土筒壁的力学性能会随温度升高发生改变,为了进一步研究在温度影响下的烟囱抗风性能,本文将继续讨论在风与温度共同作用下的烟囱动力响应分析。
混凝土在高温下的弹性模量折减系数和抗拉抗压强度折减系数选用文献[12—13]中的公式,如式(2)、(3)所示。
(2)
式中:Ec,T是高温下混凝土的弹性模量;Ec是常温下混凝土的弹性模量。
(3)
式中:fc,T是高温下混凝土棱柱体抗压强度;fc是常温下混凝土棱柱体抗压强度。
钢筋在高温下的弹性模量折减系数则选取澳大利亚规范AS4100[14]。
(4)
式中:ET是高温下钢筋的弹性模量;E是常温下钢筋的弹性模量。
3.3 烟囱风振分析结果
本节对烟囱模型施加x方向水平风荷载,对烟囱进行持续30 s风振响应分析,得到图7~8,分别为第30 s时烟囱整体水平位移曲线和第30 s时烟囱整体等效应力曲线。

图7 第30 s时烟囱整体水平位移曲线
由图7可以发现,在风荷载作用下烟囱结构自下而上,其水平位移逐渐变大,因此我们需要重视风荷载对烟囱顶部位移的影响。
通过图8可以看出,180 m烟囱的最大应力值出现在烟囱高度约80 m处,之后最大应力值随着高度升高逐渐变小。

图8 第30 s时烟囱整体等效应力曲线
3.4 烟囱受到风振与温度耦合作用的结果
本部分在得到不考虑温度的风振响应分析结果后,同时引入第二部分中温度场的计算结果,选取烟囱筒壁顶点内表面温度达到100 ℃时的整体温度场数据作为预应力场,导入风荷载分析模型中,用来模拟烟囱工作时受高温烟气影响而产生的升温过程。同时对结构进行网格划分,应保持热分析与力学分析的网格精度不变。由于混凝土与钢筋在高温下其力学性能势必会发生改变,因此有必要再次对模型进行高温作用下的风振响应分析。由此得到图9~11所示烟囱在x方向下的顶点水平位移、速度、加速度曲线。

图9 烟囱顶点水平位移时程图
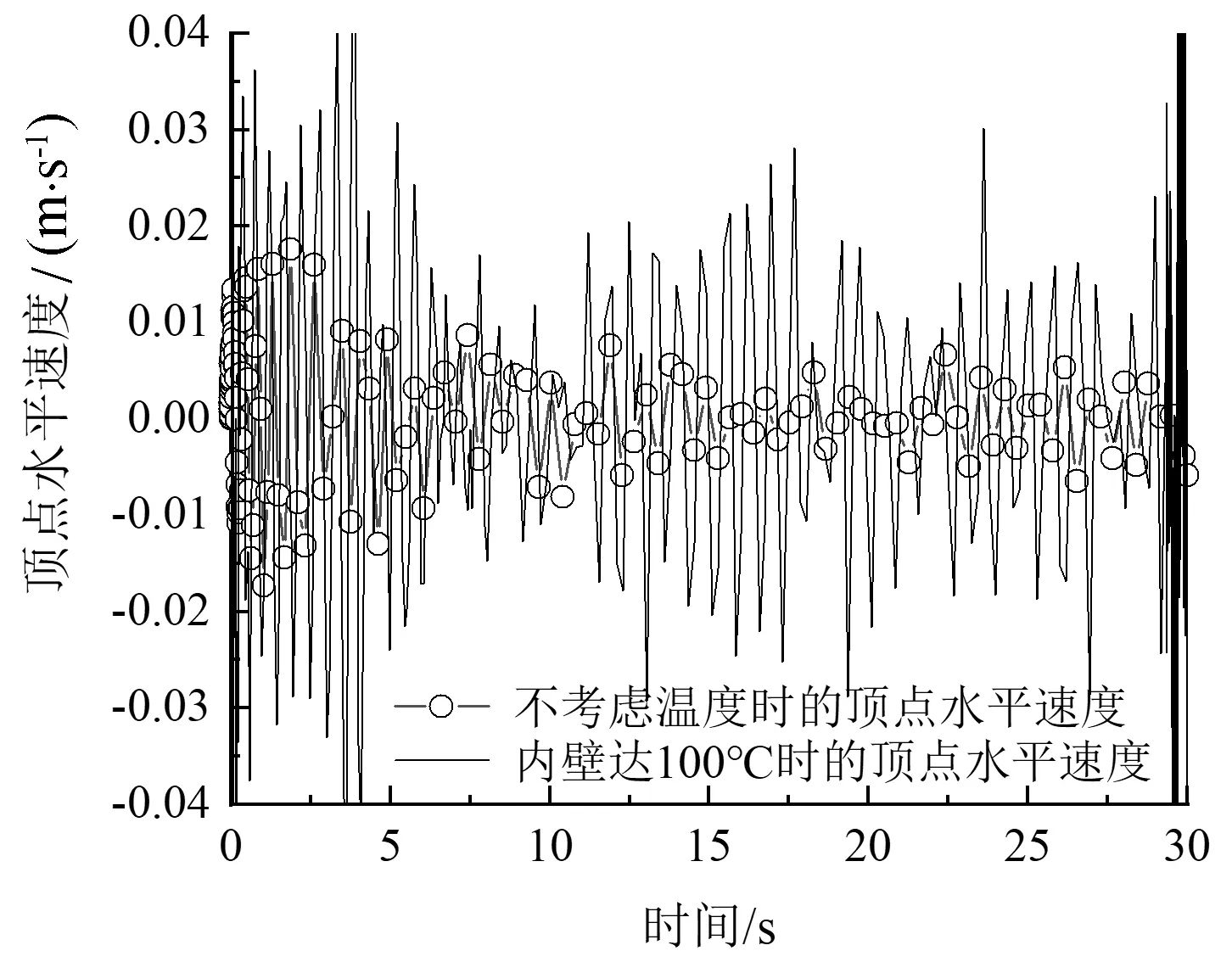
图10 烟囱顶点水平速度时程图

图11 烟囱顶点水平加速度时程图
从图9~11可以看出,考虑风与温度耦合作用后,烟囱顶点的位移曲线、速度曲线与加速度曲线会产生明显的差异。不考虑温度效应时,烟囱顶点位移极值为0.091 m,速度极值为0.017 5 m/s,加速度极值0.036 8 m/s2,而在混凝土内壁达100 ℃时,烟囱顶点位移极值为0.179 9 m,速度极值为0.032 9 m/s,加速度极值0.053 5 m/s2。
同样根据上述的计算方法,将混凝土顶点内壁达到120、140 ℃时的温度场数据,导入模型进行分析,得到的烟囱顶点水平位移、速度、加速度极值数据如表4所示。

表4 烟囱顶点风振响应极值表
从表4可以看出,在烟囱顶点内部进一步升温至140 ℃后,烟囱顶点的动力响应波动幅度进一步增大,其顶点位移极值为0.194 9 m,速度极值为0.048 3 m/s,加速度极值0.130 0 m/s2。
4 结语
本文针对某高耸钢筋混凝土烟囱进行了风振响应研究。首先对烟囱工作时的传热过程进行热传导分析,计算其温度场,得到烟囱整体的温度场数据和混凝土层内表面的升温曲线。随后利用AR滤波法获得了烟囱的风速时程。最后,通过计算烟囱内壁在3种不同高温工况下的风振响应,与不考虑温度作用时的风振模拟结果进行对比分析。得到的分析结果表明:
1)依据烟囱风振响应结果可知,烟囱顶部水平位移最大,最大等效应力出现在结构中底部。
2)高温作用下的风振响应与常温时的相比,烟囱顶点的位移、速度和加速度显著增加。
3)在高温下,随着温度进一步升高,烟囱顶点的位移、速度和加速度呈现出增大的趋势。
可以发现,高温对烟囱结构的抗风性能产生了不利影响。因此在设计烟囱等类似结构时,需要从多角度考虑,确保结构的安全性,尤其需要重视烟囱的隔热性能。

