引水渠道边坡变形特征及变形预测的研究

王 硕

(宿州市水利水电建筑勘测设计有限公司，安徽 宿州 234000)

0 引 言

引水渠道在农村饮水调度中广泛应用，渠道稳定运行是保障运行的基础。山区引水渠道建立在边坡上，土的滑坡和变形预测问题已成为当前研究热点。陈生水等以某膨胀土边坡为研究对象，通过试验手段对膨胀土的变形和稳定性进行了分析，并总结了其长期强度变形特性[1]。程展林等以某膨胀土边坡工程为背景，通过有限元软件ABAQUS建立三维数值模型，分析了膨胀土边坡的变形和稳定性[2]。陆定杰等以南阳膨胀土渠道为研究对象，通过现场勘察资料分析了南阳膨胀土渠道滑坡的破坏特征，进一步利用PLAXIS 3D有限元软件建立渠道模型，对膨胀土渠道演化机制进行研究[3]。郑东健等以某实际边坡工程为背景，分析了边坡的变形规律[4]。系统研究了多因素时变预测模型，并将现场实测数据与多因素时变预测模型的结果进行对比，验证模型的正确性。何少其等以库岸堆积层滑坡作为研究对象，分析了滑坡位移的分量响应模式，并通过多因子模型对滑坡变形进行了预测[5]。文章以某引水渠道边坡为例，基于对采取锚杆加固后的渠道边坡变形监测结果，分析渠道边坡变形规律，并结合不同预测模型，对渠道边坡变形进行预测。

1 工程简介与现场监测

文章研究的膨胀土调水工程全长共计401km，工程分布范围较广，土地的湿度及气候的湿度均变化大，渠道的稳定性较差，从而导致边坡的稳定性存在问题。渠道在桩号Y+740-Y+860段为中膨胀土，左侧渠道开挖深度范围为33-38m，渠道底部的宽度为13m，过水断面边坡坡度为1∶3；一级马道每隔6m设置一道，宽度为5m。用水泥改性土换填整个渠道，其中马道换填厚度为1.0m，过水断面换填厚度为1.5m。横断面图见图1。

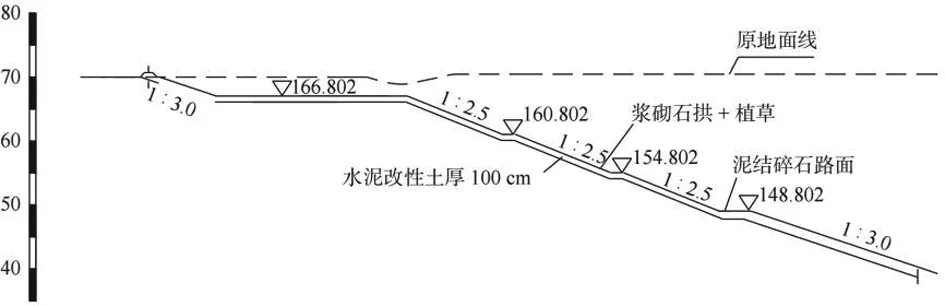
图1 构件横断面图

渠道段的所有马道都不存在大裂隙，也不存在裂隙密集带。因此在过水断面插入方桩，一级马道以上断面不设置其他抗滑桩。2016年5月，二级马道排水沟的内侧壁产生了倾斜位移；三级马道排水沟产生了断裂、沉降；三、四级马道的混凝土拱圈发生连续开裂，并且裂缝尺寸存在进一步变大的趋势，渠道出现浅层滑移现象。

勘察结果显示：Y+840的三级渠坡和Y+800的三级渠坡坡脚位置发生渗水现象，外部水分已渗入换填土层内部。在高程155m位置处，渠道边坡有一变形体，变形体深度约为2.5-7.8m。该位置发生变形的原因主要为：膨胀土未被换填层完全与外部水分隔绝，膨胀土因渗水产生裂缝并持续胀缩，渠道边坡发生蠕动变形。

为保证渠道运行期间的安全性，2016年11月，采取了一定的应急措施：安装安全监测仪器、锚杆加固、增设排水管。三级渠道边坡按3m纵向间距布置3排锚杆，锚杆呈矩形，设计锚固力为100kN，锁定锚固力>50kN。安全监测仪器主要有渗压计、测斜管等，测斜管的埋置深度范围为22-32m，图2给出了渗压计和测斜管的布置图。对于图中测点标号的含义，805-3测点定义为805桩断面上3级马道的。

2017年3月的现场监测数据表明，所采取的应急措施对渠道有一定的限制作用，但未能使渠道位移完全收敛。因此，在2016年5月，在三级渠道边坡增设伞形锚杆，共设6排锚杆，垂直方向上的锚杆间距为2.0m，顺水流方向上的锚杆间距为4.0m，设计锚固力为120kN，锁定锚固力>100kN。对新加固后的渠道边坡变形进行现场监测。

图2 给出了渗压计和测斜管的布置图

2 基于HCPC法渠道边坡分析

主成分分析和分层聚类分别简称PCA和HC，两者均为变量相似性度量工具，在主成分分析基础上开展分层聚类能更加的表述变量间关系，简称HCPC法。采用该法对渠道边坡变形进行分析。选取新加固后的渠道边坡变形数据进行分析(2017年6月—2020年5月)。图3给出了各测斜管表面测点位移过程线，图4给出了渠段环境量过程线。测斜管发生变形峰值约为0.5-2.0m的深度。按每月2次的频率观测地下水位和测斜管。图中降雨量表示每日降雨量，渠道水位表示每日平均水位。

图3 各测斜管表面测点位移过程线 图4 渠段环境量过程线

从图中可以看出，经过二次加固后的渠道边坡变形具有如下规律：向渠道内部位移渐渐变大，二级和四级马道同时产生变形，两者变形趋势基本一致，且有较好的同步响应性。不同位置的变形值均不同，呈现出显著的不均一性，二级和三级边坡在干湿循环作用下，两者的变形最为明显。渠道边坡变形首先增大随后趋于稳定，锚杆锚固力调整期间，渠道边坡变形呈飞速发展随后趋于稳定的趋势，在2017年10月后，锚杆的群锚效果逐渐发挥作用，变形发展逐渐稳定，但仍具有周期波动性。

对各测斜管位移峰值进行分析，得到变形测点分区平面映射，如图5所示。从图中可以看出，位移分布在空间上呈不均衡性，且较为明显。Y+805、Y+835位置处的渠道边坡变形为最值，独自形成一个分区。进一步结合现场查勘，Y+805位置渠道边坡在高程155m处存在滑动面，这是由膨胀土渠坡滑移导致的。

图5 变形测点分区平面映射

3 变形预测模型

3.1 指数平滑法

时间序列模型表示如下：

δ=Tt+St+Rt

(1)

式中：Tt为趋势项；St为波动项；Rt为随机项。

该方法以目前时间为起始点，通过分析历史状态预测未来状态，时间越近的数据影响越显著，同时可以避免随机干扰所带来的影响，进而开展时间序列分析。预测变形的精度受加权系数影响较为明显，提高加权系数会加快后序列额衰减，加权系数合理取值范围在0.1-0.3，当加权系数取0.2时，预测结果最精准。

该渠道所在区域浅部土层活动显著，以2016年6月—2018年11月期间观测点805-3-m位置处表明位移峰值为例，对该处位移进行预测分析。图6给出了指数平滑法分离得到的波动项和趋势项和实测值。如图所示，对渠道进行锚杆加固后，渠道边坡位移首先加速增大，随着锚杆锚固力的提升，渠道边坡位移增长逐渐趋于平缓。

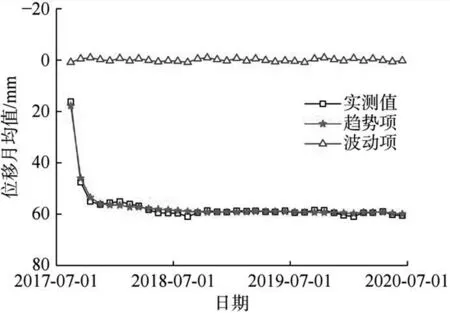
图6 指数平滑法分离得到的波动项和趋势项和实测值

3.2 自回归移动平均模型预测

自回归移动平均模型，同样是通过历史状态预测未来状态，AR和MA分别表示自回归和移动平均模型，该模型的表达式为：

(2)

式中：d为阶数(让序列平稳的差分次数)；d为>0的整数，通常情况<2；L表示滞后算子；εt为白噪声序列；φi为自回归系数，1≤i≤p，i为整数，p为自回归项；θi为移动系数，1≤i≤q，i为整数；q为移动平均项数；Xt为随机变量。

利用该模型进行变形预测时，时间序列必须得平稳，若时间序列不平稳，则需进行处理使其平稳。同样以2017年6月至2019年11月期间观测点805-3-m位置处表明位移峰值为例建立ARIMA模型，未验证模型的正确性，通过10阶交叉检验进行验证；确定所建立的模型的阶数d；建立ARIMA(1,2,2)模型，残差为白噪声，同样进行10阶交叉检验，从而对变形进行预测。其中，模型训练阶段的平均绝对误差值为0.195，模型预测阶段的平均绝对误差为0.462，模型训练阶段的平均绝对百分比误差值为0.262，模型预测阶段的平均绝对误差平均绝对百分比误差值为0.637。图7给出了实测值、模型预测值和拟合值。

图7 实测值、模型预测值和拟合值

3.3 多因素非线性回归模型

进一步建立观测点805-3-m在2017年6月至2019年11月期间的多元非线性回归模型。选取时效、地下水位、日均气温、有效降雨量、渠道水位等敏感因素，R2=0.908(模型复相关系数)，模型训练阶段的平均绝对误差值为0.923，模型预测阶段的平均绝对误差为2.830，模型训练阶段的平均绝对百分比误差值为1.022，模型预测阶段的平均绝对误差平均绝对百分比误差值为3.150。图8给出了不同影响因素对渠道边坡位移的影响程度。从图中可以看出，当采取锚杆加固后，时效为渠道边坡变形的主导因素，温度、降雨量和地下水位为渠道边坡变形次影响因素，渠道水位对渠道边坡变形影响最小。因此，在温度、降雨量和地下水位已知的基础上，构建渠道边坡变形的多因素非线性回归函数，可建立变形预测模型。

综上所示，指数平滑法适用于对加固处理后渠道变形初期的波动性和趋势性进行分析，而自回归移动平均模型和多因素非线性回归模型，可渠道变形进行预测，同时能获得不同影响因素的影响程度。

图8 不同影响因素对渠道边坡位移的影响程度

4 结 论

文章以渠道边坡为例，基于对采取锚杆加固后的渠道边坡变形监测结果，分析渠道边坡变形规律，结合预测模型，对渠道边坡变形进行预测。得到以下结论：

1)受气温、降雨等不同因素的影响，渠道边坡变形规律复杂，如不隔绝温度、降雨、地下水位等影响，运营期的渠道存在滑坡风险；

2)通过锚杆、排水孔对渠道进行加固后，渠道边坡变形前期变化显著，随后变形趋于稳定，可见所采取的加固措施效果显著；

3)指数平滑法适用于对加固处理后渠道变形初期的波动性和趋势性进行分析，而自回归移动平均模型和多因素非线性回归模型，可渠道变形进行预测，同时能获得不同影响因素的影响程度。