砂柱试验注水前初始有效应力场的生成方式研究

邢 勇

(淮滨县水利局，河南 淮滨 464400)

0 引 言

为了真实有效的实现对Liakopoulos砂柱试验模型的计算模拟，在采用FLAC3D软件进行准备时，每一步都应尽可能地与真实试验情况高度近似地对照起来。相关学者在应用该有限差分软件进行数值模拟时，也同样注重各个环节的细节处理[1-5]。蒋中明等采用FLAC3D对极端久雨条件下的软岩边坡的稳定性进行了分析研究，过程中采用Geo-studio(seep)软件的渗流计算结果导入FLAC3D软件，作者正是认识到了FLAC3D在模拟饱和-非饱和渗流场的不足，才采用另外一款在该方面有独特优势的软件的计算结果，作为初始孔压场导入FLAC3D软件中，再进行后续的模拟计算[6]。谢强等深刻理解FLAC3D软件在处理土中基质吸力问题的缺陷后，应用FISH程序进行编程，开发出了一种能够使用FLAC3D进行饱和-非饱和问题求解的方法，为FLAC3D有限差分软件的拓展使用开拓可一片新天地[7]。司宪志等D-PFC3D连续-非连续耦合的方法进行泥石流地质灾害的模拟[8]在明确了解了FLAC3D在处理颗粒类的非连续材料的局限性后，进而采用PFC软件与FLAC软件结合进行模拟计算，从而实现了颗粒材料的有效模拟[9]。陈闻潇等详细分析了FLAC3D软件进行计算时，不能模拟材料间发生分离破坏的情况，提出了一种FLAC3。冯文凯等专门针对FLAC3D不能生成饱和-非饱和渗流场的缺点，提出了一种用于在FLAC3D中生成饱和-非饱和渗流场的方法。文章作者在充分理解并熟练运用了FLAC3D中的三种生成初始有效应力场的方法后，针对在模拟Liakopoulos砂柱模型试验的试验准备阶段中砂柱中填满砂土后初始有效应力场的不同生成进行了详细分析比较，学者们可参考应用其中的方法进行初始有效应力场的生成。

1 FLAC3D计算准备

在准备进行Liakopoulos砂柱模型试验时，有一个将Del Monto砂土填筑到聚四氟乙烯圆柱桶中的过程，填筑完成后一般要静置24h以使砂土在自重作用下充分下沉固结，这一过程与采用FLAC3D对砂柱进行模拟时，在尚未设置孔隙水压力具体分布条件下，初始有效应力场的生成过程相似。与没有设置初始有效应力情况类似，在有设置了一定初始有效应力时，采用拉格朗日快速差分技术的FLAC3D软件同样提供了三种生成初始有效应力场的方法，这主要是：①在设置了一定的有效应力时，将砂柱中的砂土首先设置成弹性体，赋予其相应的弹性本构模型，再通过‘SOLVE’命令进行求解获得初始有效应力场；②在设置了一定的有效应力情况下，将砂柱中的砂土设置成真实的摩尔库伦弹塑性本构模型，但是分两步求解，第一步应用‘SOLVE’求解时，将模型材料参数中的关键参数设置成较大值，求解至平衡态，第二步应用‘SOLVE’求解时，使用与砂土材料相一致的真实的材料弹塑性参数，进行弹塑性条件下的求解，至平衡状态，获得初始有效应力场；③在设置了一定的有效应力情况下，将砂柱中的砂土设置成真实的摩尔库伦弹塑性本构模型，相应的材料参数也设置成真实的弹塑性材料参数，采用‘SOLVE ELASTIC’命令使FLAC3D软件自动进行先将材料关键弹塑性参数设置成较大值求解至平衡态，再采用真实的弹塑性材料参数求解至平衡态的过程。

2 模型构建

如图1所示的试验模型，实际试验中，聚四氟乙烯管内直径10cm，壁厚1cm，沿侧壁等间距布置测压计对试验过程中的孔隙水压力变化进行监测，而进行数值模拟试验时，主要是通过沿侧壁不同高程处设置监测点，通过获取监测点的孔隙水压力大小获得各处的基质吸力变化，聚四氟乙烯管内高102cm，砂柱填筑高度为100cm，高出的2cm主要是为了在通水后，使砂柱上方始终有2cm深的水，以使其尽快达到稳定渗流状态。试验准备时，管中主要填筑的是Del Monte砂土，每层填筑10cm，分层填筑，每层填筑控制压实度，填筑完成后，静置24h，使管中的砂土在自重作用下充分变形，以避免后续试验过程中，由于砂土自重对试验结果带来一定程度的影响。静置后，通过在管上方通稳定水流，而管上方与大气接触，但始终保持有水的状态(高出的2cm的作用)，直到水流在自重作用下沿砂柱稳定渗出形成稳定渗流后，不再对砂柱上方进行水源供应，使柱中水在自重作用下不断渗出，通过读取侧面不同高程处的孔压计获得各高程处的孔隙水压力值。

兼顾计算精度和计算时间，作者采用均值为0.1m边长的三角形网格对模型进行剖分。

图1 Liakopoulos砂柱试验设置

3 计算结果

以下分别分析比较在设置与不设置初始有效应力条件下，弹性模型、弹塑性模型变关键参数两种方式生成初始有效应力场结果。

3.1 弹性模型求解结果对比

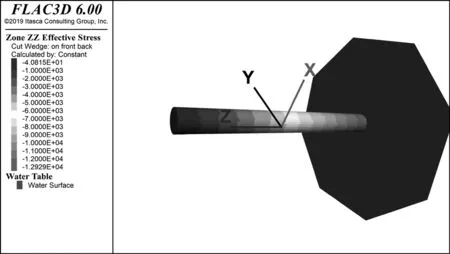
在不对有效应力给予初始值时，对材料赋予弹性模型生成的最终初始有效应力场如图2中(a)所示。由图可知，在不对有效应力给予初始值时，采用这种方法能够获得正确的初始有效应力场，计算共循环进行8195步。当对有效应力给予初始值时，对材料赋予弹性模型生成的最终初始有效应力场如图2中(b)所示。由图可知，在对有效应力给予初始值时，采用这种方法同样能够获得正确的初始有效应力场，计算共循环进行143步，几乎没有进行计算，模型就达到了平衡状态。可见，设置或不设置初始有效应力，采用弹性模型求解都能够得到正确的初始有效应力场，区别在于设置了初始有效应力，将有效缩减模型循环次数，缩短计算时间，提高初始平衡效率。

3.2 弹塑性模型变参数求解结果对比

在不对有效应力给予初始值时，对材料赋予弹塑性模型，第一步进行弹塑性求解时，将模型弹塑性关键参数设置成较大值，以近似弹性求解，第二步更改材料关键参数的值，进行弹塑性求解，生成的最终初始有效应力场如图3中(a)所示。由图可知，在不对有效应力给予初始值时，采用这种方法能够获得正确的初始有效应力场，计算共循环进行8198步。当对有效应力给予初始值时，对材料赋予弹塑性模型，第一步进行弹塑性求解时，将模型弹塑性关键参数设置成较大值，以近似弹性求解，第二步更改材料关键参数的值，进行弹塑性求解，生成的最终初始有效应力场如图3中(b)所示。由图可知，在对有效应力给予初始值时，采用这种方法同样能够获得正确的初始有效应力场，计算共循环进行144步，几乎没有进行计算，模型就达到了平衡状态。可见，设置或不设置初始有效应力，采用弹塑性模型变关键材料参数求解都能够得到正确的初始有效应力场，区别在于设置了初始有效应力，将有效缩减模型循环次数，缩短计算时间，提高初始平衡效率。

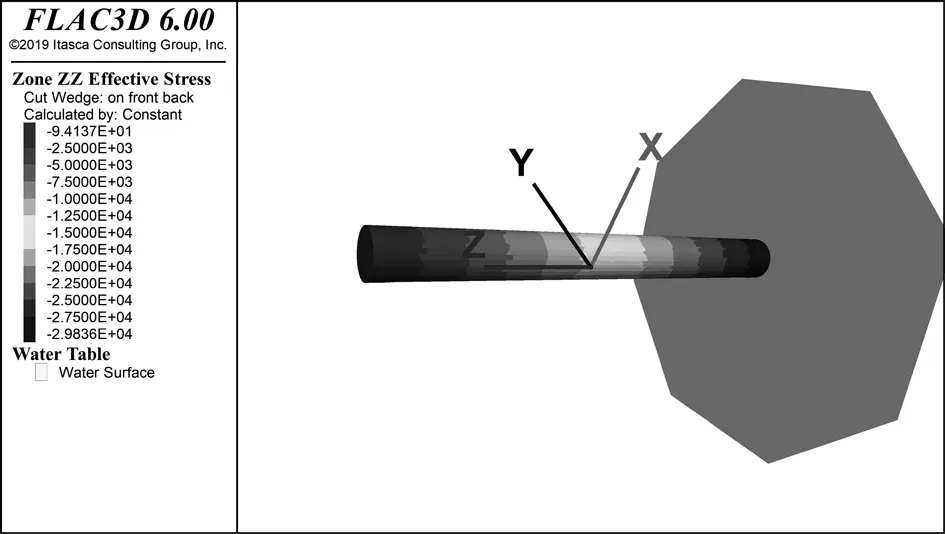
(a)不设置初始有效应力时求解结果 (b)设置初始有效应力时求解结果

(a)不设置初始有效应力时求解结果

(b)设置初始有效应力时求解结果

4 结 论

在设置和不设置初始有效应力时，通过对比两种生成初始有效应力场的方式，得出结论：

1)在设置和不设置初始有效应力时，弹性模型、弹塑性模型变关键参数两种方式均可以获得与真实情况相符的正确初始有效应力场。

2)相比不设置初始有效应力时，设置初始有效应力时的计算效率显著提高。

3)建议采用不设置初始有效应力、弹性或弹塑性变关键参数的方式生成初始有效应力场。