疏松砂岩储层油井污染规模定量评价方法设计

王晓超，郭小哲，刘全刚，王 壮，崔国亮，韩立杰，李含秀

(1. 中海油能源发展股份有限公司工程技术分公司，天津 300452；2. 中国石油大学(北京) 石油工程学院，北京 102249)

疏松砂岩储层一般表现为基质胶结疏松，泊松比较大(大于0.28)，弹性模量较小(小于1 GPa)，轴向抗压强度较小(小于5 MPa)，孔隙多为高孔高渗特征，储层中的原油黏度一般较大(大于50 mPa·s)，生产时多采用井底防砂并控制生产压差措施，以抑制出砂带来的停泵故障[1-3]。即便如此，由于修井、酸化、注水、注聚[4]等措施的应用，许多井不同程度地受到了污染，产液量大幅下降，给生产带来了不利影响[5-6]。

疏松砂岩储层伤害[7-8]既有来自于通过井筒的钻完井、酸化、大修、防砂等作业型外向污染，也有来自于注入流体的水敏、速敏、油水乳化、黏土或胶团[9-11]等驱动型的内向污染。外向污染一般深入地层区域较小(约1～2 m)，可以通过小型酸化进行改善[12]；内向污染由于受到注入流体的长期作用，往往影响区域较大，规模小的井下措施难以取得很好效果，有的需要大型压裂措施才能使井的产能得以恢复[13]。

压裂是通过人工造缝的方式，穿过污染区使井筒和储层高效连通，降低渗流阻力，使原油能够顺畅地流入井中。压裂的裂缝长度和导流能力则需要油井附近储层的污染规模来确定。

常用的储层污染的判别方法是试井[14-15]，它能够通过测试油井开井或关井的井底压力随着时间的变化规律得到污染区的半径和渗透率，进而可以评价污染程度。但试井往往需要向井内下入专用的设备，而且对井筒的工况有一定要求，若进行关井测试还需要停产。因此，油田上许多井(除去最初的试油试采之外)并没有相关的试井资料，也就没有第一手的资料用于评价污染规模。

在储层污染评价方面，李柏鹏等[16]提出通过不试井近似地得到储层污染程度的方法，采用堵塞比和表皮附加压降表征了储层近井地带的污染程度；徐天燕等[17]通过对声波测井曲线分析评价了砂岩段受污染是引起试井结果不理想的原因；庄登登等[18]根据煤层气压裂曲线中油压曲线到达破裂压力后下降行迹特征计算出储层渗透率损害比；范俊强等[19]建立了以污染区储层渗透率呈指数变化的数学模型，绘制出双孔裂缝性砂岩污染储层井底压力响应特征曲线；路士华等[20]建立了多孔介质内微粒启动、运移、堵塞的数学模型，预测了由于油层出砂造成的油层伤害过程及伤害程度。

前述研究中，多采用了专业的测试(如试井、测井、压裂)才能得到污染评价，成本高而且工期长，影响正常生产；另一些需要建立复杂的数学模型，求解和计算难度相对较大，对参数的需求多而且要求精度高；此外，疏松砂岩的污染规模定量评价研究较少。基于以上分析，该研究根据高孔高渗的疏松砂岩油井的产量降低幅度，应用裘比公式及表皮系数计算公式，辅助油藏数值模拟，设计一套用于计算储层污染程度和污染半径的简便快捷的污染规模评价方法，为后续压裂或者其他增产措施的分析提供依据。

1 地层模型

疏松砂岩储层胶结差，孔隙中流体流动速度快，长期注水会引起近井区域的砂堵，特别是聚合物驱后砂粒、高黏弹性的高分子化合物以及原油胶质和沥青质的共同作用常会形成的胶团，在油井附近区域聚集和沉积而形成堵塞，由此导致油井产量大幅下降而影响生产。因此，设计油井污染后的理想模型如图1所示，实际油井按井网方式可近似等效为圆形供给边界中心一口生产井，污染区域把储层分为内区和外区2个渗流区域，外区是原状地层，内区则是受污染地层，用于评价内区的2个主要参数是染污半径rs和染污程度Ds(渗透率损失程度，实质上是内区渗透率的变化)，假设储层内是单相液体稳定渗流。已知原状地层的属性及产液量的变化，需要确定的是污染半径和污染程度。

图1 复合油藏物理模型示意图Fig.1 Schematic diagram of composite reservoir physical model

由于通过井筒作业产生的外向污染半径一般较小，污染程度较大，容易识别，也容易处理。但由于储层内部的流体流动带来的内向污染过程缓慢，机理复杂，污染半径一般较大，污染程度不易确定，对油井的影响很大，污染规模的评价是改造措施的重要参考依据。因此，该文重点研究疏松砂岩的内向污染。

2 拟合油藏参数

疏松砂岩油层厚度大，生产小层多，纵向上的非均质严重，主力油层的渗透率可高达6 000 mD，非主力油层的渗透率有的仅有几百，而油井的产量变化是多个油层综合的结果，因此，为了使计算的参数能够真实地反映储层的特征，在计算前需要进行油藏参数拟合，其中渗透率是关键参数。由于油井射开的产层一般包括多个小层，平均渗透率采用有效厚度加权方法初步确定。

(1)

式中：k为平均渗透率，mD；ki为第i小层的渗透率，mD；hi为第i小层的有效厚度，m；n为油井射开的小层数。

假设储层单相液体流动，则圆形供给边界油藏中心一口井的产量可以由裘比公式[21]得出：

(2)

式中：Q为油井污染前产量，m3/d；μ为地下液体黏度，(mPa·s)；h为油层总有效厚度，m；pe为原始地层压力，MPa；pw为井底流压，MPa。re为供给半径，m；rw为井底半径，m。

应用已知的油藏参数及所求得的平均渗透率计算污染前的理论产量，当所得结果与实际油井产量不一致时，可根据储层及油井的属性再次确认黏度、生产压差、供给半径和井底半径等参数的正确与否，然后调节平均渗透率，实现油藏参数的拟合。

3 污染程度的确定

疏松砂岩储层中的许多产量大幅下降的油井即使经过井底冲砂或者小型酸化等措施，仍然不能较大程度改善，说明引起产量下降的主要原因是内向污染，其污染半径一般较大(20 m以上)，污染程度相对较低(80%以下)。基于此，当油井受到污染时，可以假想为近井一定区域内的渗流阻力增加，引入表皮系数(也称为附加阻力)，污染后油井产量的裘比公式为：

(3)

式中：Q′为油井污染后的产量，m3/d；S为油井的表皮系数，无量纲。

油井污染后的产量是已知的，假设生产压差不变，由式(3)可以求表皮系数S，即：

(4)

如果把污染后的储层简化为复合油藏模型，即储层分为没有受污染的外区和受到污染的内区两部分，此时，表皮系数S可以表示为[22]：

(5)

式中：ks为内区的平均渗透率，mD；rs为内区半径，m。

由平面径向渗流理论可知，压力沿径向r的分布呈现漏斗形状，即近井压降幅度要明显大于远井，能量主要消耗在近井区域。有压力分布公式：

(6)

式中：p(r)为距离井底r处的地层压力，MPa；r为距井底距离，m。

应用式(6)计算不同半径r内的压降比例表明，不超过20 m，压降损失可达70%以上，由此，通过式(5)计算污染参照半径rsc=20 m时的污染区渗透率ks，定义污染程度Ds为：

(7)

式中：Ds为污染程度，无量纲。

4 污染半径的确定

结合压降损失的特征，疏松砂岩的内向污染在20 m的假想内区半径范围里所形成的污染具有代表性，但不同的渗透率、不同的污染程度、不同的产量降低幅度下，实际污染半径是有差异的，因此，实际的污染半径需要在假想内区半径20 m的基础上进行修正。

根据疏松砂岩储层的特征建立油藏数值模拟模型，渗透率选取2 000 mD，1 000 mD和500 mD，污染半径20 m，油水井间距350 m，生产压差3 MPa(疏松砂岩油井生产压差一般低于5 MPa)，模拟得到的不同污染程度引起的产量降低幅度见表1。

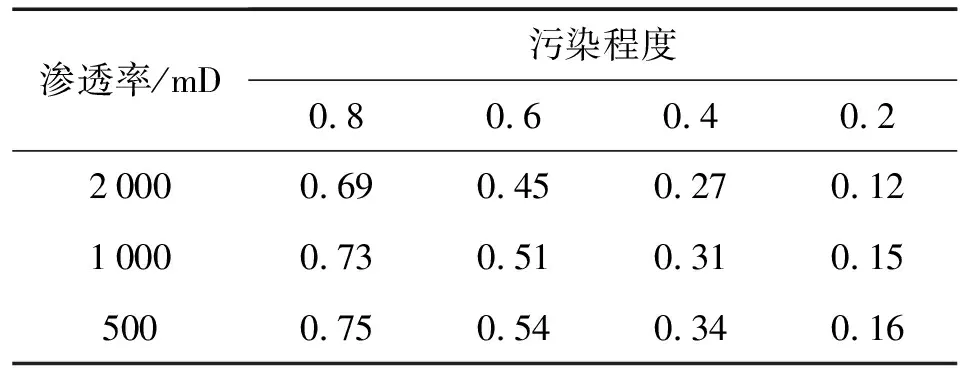
表1 不同污染程度产生的产量降低幅度Table 1 Decrease of output caused by different pollution levels

表中，产量降低幅度计算公式为：

(8)

式中：RQ为产量降低幅度，无量纲；Qs为污染后产量，m3/d；Qi为污染前产量，m3/d。

由表1可知，储层渗透率越低，近井污染对油井产量的影响越大，相同渗透率时污染程度越大带来的产量降低幅度也越大，而且是近似直线变化。以数值模拟的结果为依据进行实际井的污染半径的修正。

首先，根据之前拟合得到的渗透率应用插值方法求得不同污染程度时的产量降低幅度，公式为：

(9)

式中：RQ k为目标储层原渗透率对应的不同污染程度的产量降低幅度，无量纲；RQ n e为插值时后一个产量降低幅度，无量纲；RQ p r为插值时前一个产量降低幅度，无量纲；kn e为插值时后一个渗透率，mD；kp r为插值时前一个渗透率，mD。

然后根据已求得的污染程度Ds再次应用插值方法求得对应的理论产量降低幅度RQ r，公式为：

(10)

式中：RQ r为油井污染后理论产量降低幅度，无量纲；RQ k n e为插值时后一个产量降低幅度，无量纲；RQ k p r为插值时前一个产量降低幅度，无量纲；Dn e为插值时后一个污染程度，无量纲；Dp r为插值时前一个污染程度，无量纲。

油井实际产量降低幅度RQ a为：

(11)

式中：RQ a为油井污染后实际产量降低幅度，无量纲。

径向渗流时，产量Q与自然对数呈线性关系，定义污染区自然对数与产量降低幅度存在如下关系：

(12)

式中：rs c为参照污染半径，其值为20 m；

得到油井修正后的污染半径为：

(13)

5 效果分析

某海上油井的目标储层是典型的疏松砂岩储层，顶深1 329 m，油层厚度为58.9 m，地下原油黏度为90 mPa·s，供给边界半径350 m(约为井距)，注水保持地层压力为14.2 MPa，生产压差为2.2 MPa(低于地饱压差2.28 MPa)，井底半径0.1 m。该井采出方式为ESP生产，由于泵故障及出砂，产量大幅下降，进行大修及近井解堵后，产量恢复效果不明显，认为该井属于内向型污染。污染前产液量平均为283 m3/d，压裂前平均为110 m3/d，油井实际产量下降幅度61.13%。为了能给后续压裂改造规模设计提供依据，需要对污染程度和污染半径进行定量分析。该井生产层段共有11个小层，细分小层后的有效厚度和渗透率见表2。

表2 该井生产层段的渗透率分布

按有效厚度加权计算平均渗透率为2 965 mD，拟合污染前的产量，得到拟合渗透率为2 958 mD。

由拟合渗透率计算污染后的产量，得到表皮系数为12.85，进而可求得污染半径为20 m时的污染区渗透率为863.72 mD，由此计算得到污染程度为0.708。

由拟合渗透率进行插值，得到污染程度对应的产量降低幅度，再根据已经确定的污染程度进行插值得到理论产量降低幅度为53.59%，进而求得污染半径为42.17 m。

由以上计算，该井的污染规模定量评价结论是：污染程度0.708,污染半径42.17 m，产量下降幅度61.13%。对该模型进行数值模拟验证，其产量下降幅度为60.21%，误差0.83%，说明该结果是可信的，该方法是可行的。

现场实际压裂分了两段，裂缝半长分别是46.1 m和37.6 m，平均裂缝导流能力都在150 D·cm以上，压后的产液量可达240 m3/d，几乎恢复到污染前的产量，实践结果进一步验证了该文方法的可靠性。由该方法求取的污染半径可以作为确定最小压裂裂缝半长的依据，污染程度可以作为确定导流能力的参考。

6 结论

1)疏松砂岩储层油井易受到堵塞而被污染，引起产油量大幅降低，污染规模的定量评价是压裂解堵的重要参考依据，简单便捷的计算方法提供了低成本、高效率、易操作的分析手段；

2)疏松砂岩储层渗透率较低时，储层污染对产量的影响相对较大，相反，渗透率越高时带来的产量降低幅度较小，但渗透率低时的产液量低，渗透率高时的产液量高，因此，从对产油量的影响上看，虽然渗透率高的产液量降低幅度较小，但其初始的产液量是较高的，也就形成对产油量的影响可能更大，反映到选井上时更应该重视高渗储层污染的压裂改造；

3)污染程度的确定是设置了参照污染半径20 m，选取该参照的理由是20 m内的压降占到总压降的70%以上，也就是20 m以内的压降基本反映了油井的污染程度；

4)污染程度和污染半径的求取结果得到了数值模拟的验证，现场实际井的压裂论证了方法的可靠性。