欧标铁路货车制动转换装置设计方法
张建峰,王小飞,李响响,李 政,桑兴华
(中车山东机车车辆有限公司,山东 济南 250022)
0 引言
欧标铁路货车制动系统中,通常安装有各种转换装置,例如G-P转换装置和ON-OFF转换装置。这类转换装置通常在车体两侧都安装有操作手柄,两侧手柄通过转轴连接,并在转轴和相对应的阀上都安装有转换拨叉。当操作手柄切换至一个工作位置时,与其相连的阀也切换至相应的工作位置。
在设计转换装置时,需要对转轴和阀之间的连杆进行设计。在对连杆进行设计时,以前往往采用试凑法或三维软件求解方法。试凑法就是通过不断改变连杆的长度,试凑出合适的连杆,存在设计周期长、设计不够精确的问题。而使用三维软件求解,存在对软件依赖性强、漏解的问题。
本文针对以往设计制动转换装置时存在周期长、精确度差、漏解等问题,提出使用几何求解和数值求解两种系统、精确并且操作简单的设计方法,完善了欧标铁路货车制动转换装置的设计方法,方便了设计人员对转换装置的设计工作,减少了设计成本和周期。
1 几何求解法
图1为欧标铁路货车制动系统中常见的G-P转换装置和ON-OFF转换装置。对该转换装置进行设计时,首先应确定阀和转换装置的位置,然后对连杆进行设计。其基本的设计原则是在切换至不同功能位置时连杆的长度相等。

图1 转换装置
ON-OFF转换装置示意图如图2所示,转动手柄将转换装置切换至ON位和OFF位时连杆的长度是相等的。该装置本质是四杆机构,两处拨叉即为四杆机构的连架杆,连杆即为四杆机构的中间连杆。在转换装置中,阀上拨叉的初始角度和转动角度以及转换装置上拨叉的转动角度都为已知量,即在此四杆机构中,只有中间连杆长度及主动杆的初始角度为未知量,其余都为已知量。
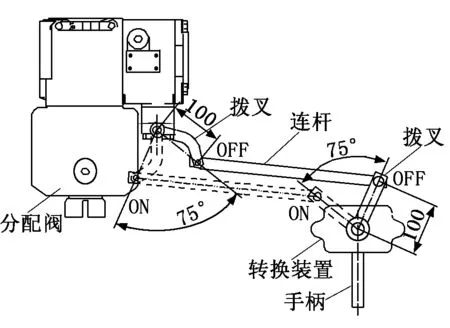
图2 ON-OFF转换装置示意图
在一般的转换装置中,两个拨叉的长度是相等的,并且在功能转换的过程中两个拨叉的转动角度相同。例如图2所示的转换装置中,阀上拨叉长100 mm,转动角度为75 °,转换装置上拨叉的长度也为100 mm,转动角度也是75 °,即在此四杆机构中两个连架杆长度和转动角度都相同。
四杆机构中的平行四边形机构或逆平行四边形机构由于正好满足两个连架杆长度相同并且角速度相同的要求,因此利用平行四边形机构的特性,使用几何法对转换装置中的连杆进行简单的设计。
当两个连架杆的转动方向相同时,即同为顺时针或是同为逆时针转动时,转换装置可简化为如图3所示的四杆机构。阀上拨叉简化为连架杆AB是从动杆,转换装置上拨叉简化为连架杆DC是主动杆,此时可将转换装置设计成平行四边形机构。首先确定固定点A、D的位置,然后确定从动杆的两个工作位置,即B点和B′点,然后以A点为基点,分别将AB的AB′平移至D点形成线段DC和DC′,分别连接BC和BC′就得到该四杆机构的两个工作状态,根据平行四边形机构的特性,机架的长度LAD即为中间连杆LBC的长度。
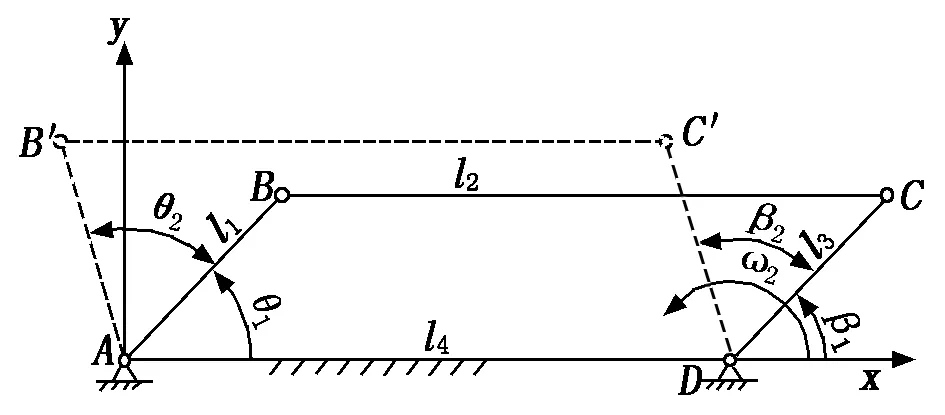
图3 平行四边形机构示意图
当两个连架杆的转动方向相反时,转换装置可简化为如图4所示的四杆机构。AB为从动杆,DC′为主动杆,此时可将其设计成逆平行四边形机构。确定A、D及B点和B′点位置后,分别以B点和B′点为基点,将AB和AB′平移至D点形成线段DC′和DC,分别连接BC′和B′C就得到该四杆机构的两个工作状态。图4中AB//DC,AB′//DC′,此时BC′的长度就是中间连杆的长度。
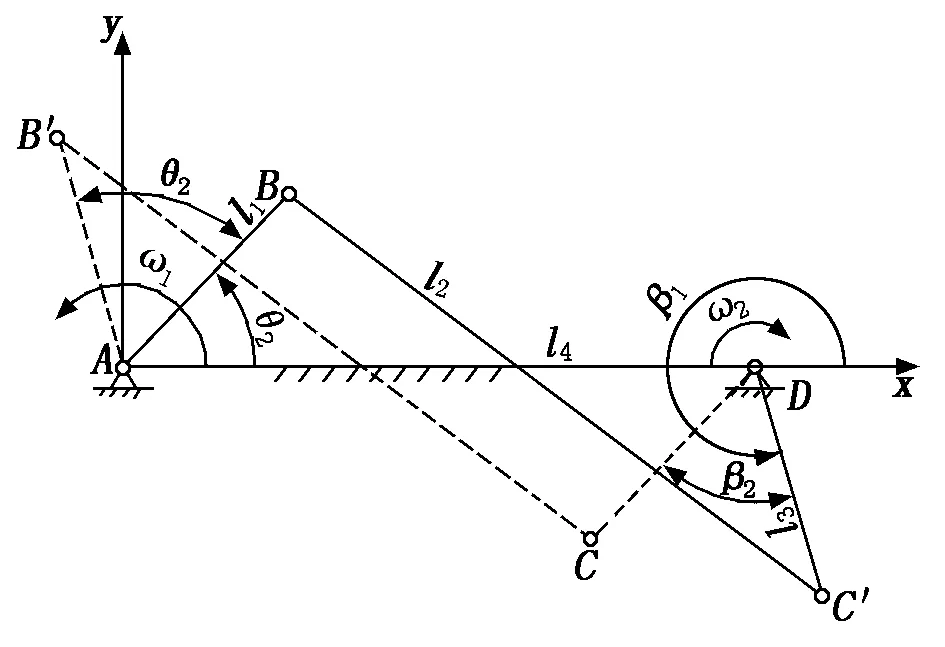
图4 逆平行四边形机构示意图
利用几何法对转换装置进行求解,方法简单明了,虽然摆脱了对软件的依赖,但同样存在漏解的问题,解出的连杆有时也存在干涉、传动角过小等问题,并且当两个连架杆长度或是转动角度不同时,该方法并不适用,这就需要用更精确的数值计算的方法对该机构进行系统设计选型。
2 数值计算求解法
图5为出口欧洲某铁路货车中的制动开关转换装置示意图,阀上拨叉长88 mm,两个工作位置间夹角为90 °,而转化装置上拨叉长100 mm,转化装置处转角为75 °,此时几何求解法就不适用于该机构,应采用数值计算的方法对其进行求解。

图5 制动开关转换装置示意图
两个连架杆转动方向相同时可简化为图6所示的机构,AB和AB′为阀上拨叉的极限位置,CD和C′D为转换装置上拨叉的极限位置。根据实际条件可知l1、l3、l4、θ1、θ2、β2已知,主动杆的初始角度β1、连杆长度l2以及α1、α2为未知量。
2.1 闭环矢量方程求解
根据已知条件,可以得出闭环矢量方程式如下:
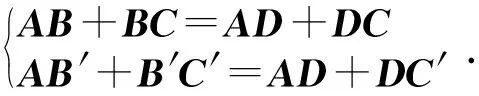
(1)
将闭环矢量方程在x轴和y轴方向上分解可以得到:
(2)
式(2)为四元一次方程组,通过对其求解,就可以得到主动杆初始角度β1和连杆长l2。

图6 两连架杆转动方向相同时机构示意图
2.2 杆长不变原则求解法
式(2)中变量较多且有较多的三角函数,求解过程较复杂,根据连杆长度不变的原则,可对该机构建立简单的求解方程。在如图6所示的平面坐标系中,可以得到各点的坐标:
(3)
中间连杆长度保持不变,即:
LBC=LB′C′.
(4)
将相关坐标代入式(4)可以得到式(5):
[l4+l3cosβ1-l1cosθ1]2+[l3sinβ1-l1sinθ1]2=
[l4+l3cos(β1+β2)-l1cos(θ1+θ2)]2+
[l3sin(β1+β2)-l1sin(θ1+θ2)]2.
(5)
式(5)为一元一次方程,求解较简单,求得主动杆的初始角度β1后代入式(6)中,可求得连杆l2的长度:
l2=(l4+l3cosβ1-l1cosθ1)2+(l3sinβ1-l1sinθ1)2.
(6)
利用式(5)对如图5所示的转换装置进行求解,对其建立如图7所示的坐标系,得到l1=88 mm,l3=100 mm,l4=234.17 mm,θ1=16.21°,θ2=90°,β2=75°。
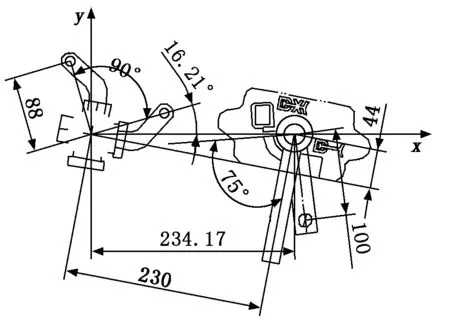
图7 转换装置坐标系示意图
将已知数据代入式(5)中,求得β1=25.8°或β1=86.99°,将β1计算结果代入公式(6)中可求得l2=240.5 mm或l2=172.3 mm。通过绘图验证结果,如图8所示,得出此计算方法是准确可靠的。然后可以根据实际的要求选取合适的结果对机构进行设计。
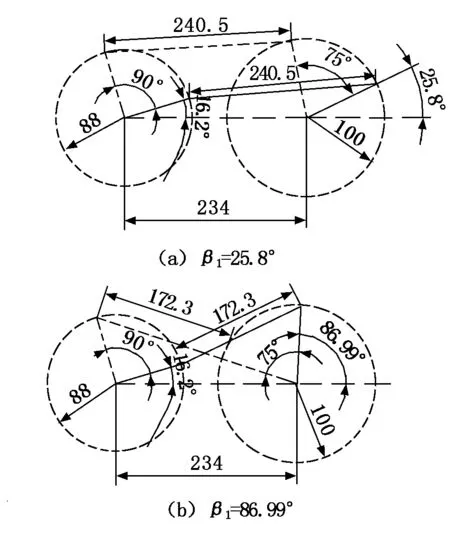
图8 结果验证示意图
当两处连架杆转动方向相反时的机构简图如图9所示。
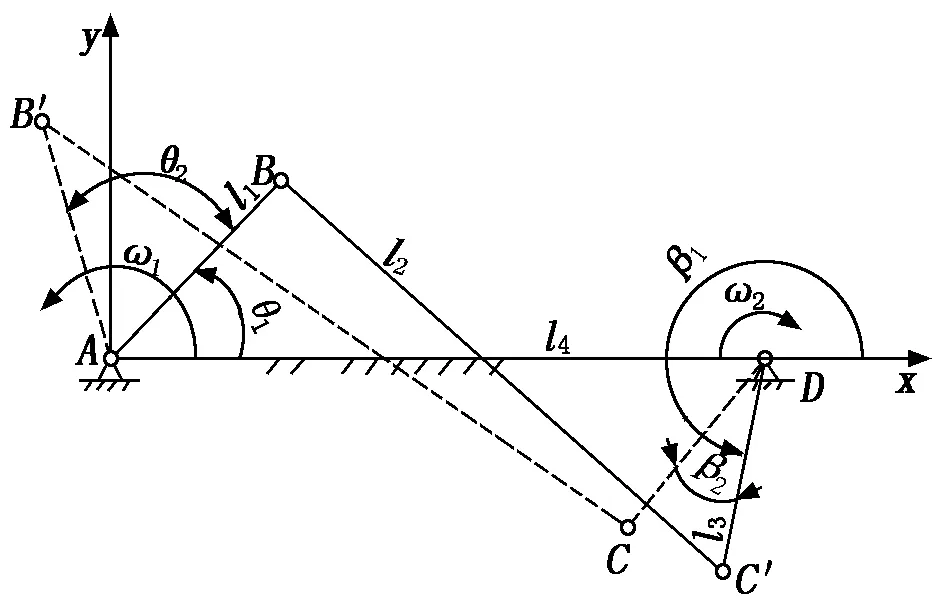
图9 两处连架杆转动方向相反时的机构简图
此时式(5)根据几何关系更改为式(7),即可求解β1和l2。
[l4+l3cosβ1-l1cosθ1]2+[l3sinβ1-l1sinθ1]2=
[l4+l3cos(β1-β2)-l1cos(θ1+θ2)]2+
[l3sin(β1-β2)-l1sin(θ1+θ2)]2.
(7)
需要注意的是,当使用数值计算法进行求解时,若存在求解不出实数解或是得到的结果不能满足使用要求的情况,此时就需要对l4的尺寸进行优化。
使用数值计算法对转换装置进行求解,可以得到满足要求的全部解,并且适用于特殊尺寸转换装置的求解,相较于几何法,该方法更系统科学和准确。
3 结论
本文针对欧标铁路货车制动系统中转换装置连杆设计困难的问题,提出几何和数值计算求解两种简单、系统和精确设计方法,克服了以往设计方法周期长、精确度低等问题,完善了转换装置的设计方法,方便设计人员以后对制动转换装置进行设计,大大减少了设计成本缩短了产品开发周期。

