城市公共交通出行方式选择博弈模型

李陈洋，雷爱国，吴啸宇，洪 泰

(南京理工大学 自动化学院，南京 210094)

轨道交通和常规公交是城市客运交通的基础，其中轨道交通相比常规公交具有运行速度快、荷载能力强等特点，构成了许多城市公共交通线网的“骨架”，但在一些工作地点相对集中地区轨道交通可达性明显低于常规公交。因此，合理分配公共交通资源、优化公共交通出行结构、提高公交服务水平会对社会建设和发展产生深远影响。目前，博弈演化理论、不确定性模型以及约束规划等先进的数学思想被广泛应用于公共交通的出行选择问题中[1-2]。

1973年，Maynard等[3]和Smith等[4]将博弈论的基本理论与生物进化现象相结合，提出了演化博弈理论中具有里程碑意义的均衡概念：进化稳定策略(ESS)，该理论也成为演化博弈理论的基石。国外学者研究大都集中在交通出行行为选择问题上：Golob[5]考虑了人口密度对出行方式选择的影响，研究表明人口密度对出行方式的划分密切相关；Bento等[6]分析了城市空间结构对出行需求的影响，解决了城市形态、道路密度对通勤方式选择的影响；Koryagin等[7]基于logit模型研究了乘客出行方式，证明了乘客与交通管理者之间存在纳什均衡；Syahlendra[8]以三种交通出行方式为背景，基于离散选择模型对调查结果进行回归分析，得到不同交通方式的划分主体；Yin等[9]从出行行为角度分析公共交通出行时空特征，研究了公共交通出行行为的影响因素。国内学者在博弈论应用出行方式选择的问题上研究较多：蔡鉴明等[10]建立考虑出行者异质特性和城市交通运行状态的演化博弈模型,使用多智能体仿真方法研究引入共享交通后的城市居民中长距离出行方式演化过程；周雨阳等[11]对地铁公交线路合作博弈进行研究，表明合作收益分配模型可以公平合理地分配合作收益；王桂鹏[12]基于前景理论对城市交通出行方式选择的演化博弈进行分析；武晓晖等[13]把交通方式的选择和是否接收低碳理念作为策略的两个维度,建立了居民低碳出行多维博弈模型；刘晧等[14]考虑政府介入因素,分析出租车出行方式选择的演化博弈。在道路阻抗函数理论研究方面，我国学者基于经典的BPR(美国联邦公路局函数)，提出了符合我国国情的回归道路阻抗函数模型[15]。

总的来看，现有研究成果在考虑出行者公共交通方式选择时，一方面，单一考虑出行成本对交通方式选择的影响；另一方面，仅用少量参数定义出行收益作为博弈矩阵的收益，没有用符合具体情况的参数来量化出行成本涉及到的影响因素。为进一步完善博弈理论在公共交通方式选择上的研究，应将出行收益与出行成本结合，更加综合全面地看待问题。因此，文中首先依据出行影响因素构建出行成本函数；其次，对两类出行者不同出行方式的出行收益进行量化，在计算道路交通出行时间时，引入BPR路阻函数计算通行时间建立道路出行者出行时间与交通流量之间的关系；最后，创造性的将两者结合，既考虑了出行收益也考虑了出行过程中出行影响因素对出行的影响，结合仿真分析证明所建模型的合理性。

1 演化博弈模型构建

演化博弈论是将经典博弈论与演化理论有机结合而产生的一种理论[16]，主要包括群体和在每一个群体中对应的各自行动集合；收益函数(pay off function)是群体采取某一种策略时获得的收益；复制动态则反映群体参与者的学习、模仿过程；均衡(equilibrium)反映演化的收敛演化动态，包括静态的ESS(演化稳定策略)、动态的EE等概念。

1.1 出行成本函数建立

出行者的出行成本主要包含时间、货币两个因素。随着生活水平的提高，现代居民也同时更加注重出行质量，为使模型更符合实际情况这里再引入舒适度这一指标，为使三个不同变量单位统一，对舒适度、出行费用做归一化处理，具体成本函数为[17]

θi=Ti+αiCi+βiEi

(1)

式中：θi为出行者选择第i种交通方式时的出行成本，元；Ti为出行者选用第i种交通方式时的乘车时间，min，乘车时间计算分为两种情况，选择常规公交方式的应根据分担的交通流量由道路阻抗函数求出行驶时间，选择轨道交通方式的出行时间一般为定值，则由调查轨道交通运行不同时段表所得；Ci为出行者选择第i种出行方式的舒适度；Ei为出行者选择第i种交通方式时的出行费用，元；αi，βi分别为出行费用、出行舒适度在第i种交通方式的时间价值系数(反映交通方式的时间效用)。

查阅相关文献资料[17]，交通方式的舒适程度取决于所乘交通工具的拥挤程度，以每位乘客平均所占的有效面积表示拥挤程度，在文中所选的模型中分别采用出行费用的10%和20%作为舒适度成本，主要分为3个等级，其评判标准如表1所示。

表1 拥挤度评价标准

1.2 道路阻抗函数

1966年美国联邦公路局对大量路段进行交通调查，从而根据收集到的交通数据回归分析出道路行程时间与流量的关系式，后来应用广泛且被称为BPR路阻函数模型(见图1)。其对道路阻抗的实质把握非常准确，且具有良好的数学性质，数学表达式为[15]

(2)

式中：t为车辆在道路中行驶时间；t0为路段的自由流行程时间；Q为路段的车流量；C为路段的实际通行能力；α，β为模型待定参数，文献建议取α=0.15,β=4.0。

图1 BPR函数

以上是与美国道路相适应的道路阻抗函数，可以看出它只考虑了机动车流量对道路产生的影响。但我国交通状况复杂，呈机非混行的交通特点，针对这些情况，国内学者提出了适应我国国情的道路阻抗函数模型为[15]

(3)

式中：V1，V2为机动车、非机动车路段交通量，辆·h-1；C1，C2为机动车、非机动车路段实际通行能力，辆·h-1；k1，k2为回归参数，均大于0。

1.3 博弈模型构建

在博弈模型的构建中最主要的元素有：收益矩阵，其用来描述两个或多个参与对象的策略和支付矩阵；复制动态方程，用于描述某一特定策略在一个种群中被采用的频数或频度的动态微分方程；演化稳定策略，用于分析动态复制方程随参数变化的收敛。在构建一个完整的博弈模型前，为了对处于不完全信息中的演化稳定性进行分析，首先结合要分析的对象做出以下六点假设：

假设一：在博弈模型中，分别将时间敏感度的强、弱看作一个整体，两者在博弈中被视为独立个体，各自追求利益最大化。

假设二：假定出行者从出发到目的地仅有常规公交和城市轨道交通两种交通方式选择。

假设三：在选择公共交通出行方式时，时间敏感度不同的双方可以根据自己的情况，合理选择自身的行为，即博弈模型的策略集有{常规公交，常规公交}、{常规公交，轨道交通}、{轨道交通，常规公交}、{轨道交通，轨道交通}。

假设四：设定时间敏感度强出行者选择常规公交的比例为x，选择轨道交通的比例为1-x；而时间敏感度弱出行者选择常规公交的比例为y，选择轨道交通的比例为1-y。

假设五：当两种出行者选择的交通方式相同时，时间敏感度强的出行者基本收益将损失a，时间敏感度弱的出行者基本收益损失b，但当两类出行者选择不同交通方式博弈时不会造成任一方损失，且a>b。

假设六：假设时间敏感度强出行者选择常规公交出行获得的收益为A1(例如车费收益及满足出行需求目的所获得收益)，选择轨道交通出行获得的收益为A2(例如时间效益及满足出行者舒适度需求所获得收益)；同理，时间敏感度弱出行者分别选择两类出行方式所得出行收益为Bi(i=1,2)，意义同上。

基于以上假设，便可以得到在考虑出行成本情况下对时间敏感度不同的两类出行者的出行收益演化博弈模型矩阵，如表2所示。

表2 两类出行者出行收益演化博弈矩阵

2 博弈均衡分析

由于时间敏感度弱的出行者选择常规公交的概率为y，则选择轨道交通的概率为1-y；时间敏感度强的出行者选择常规公交的概率为x，则选择轨道交通的概率为1-x。假设时间敏感度强出行者选择常规公交的期望收益为f1，选择轨道交通的期望收益为f2，平均收益为f12[18]。

f1=y(A1-T1-α1C1-β1E1-a)+

(1-y)(A1-T1-α1C1-β1E1)

(4)

f2=y(A2-T2-α2C2-β2E2)+

(1-y)(A2-T2-α2C2-a)

(5)

f12=xf1+(1-x)f2

(6)

同理，时间敏感度弱的出行者选择常规公交的期望收益为f3，选择轨道交通的期望收益为f4，平均收益为f34。

f3=x(B1-T1-α1C1-β1E1-b)+

(1-x)(B1-T1-α1C1-β1E1)

(7)

f4=x(B2-T2-α2C2-β2E2)+

(1-x)(B2-T2-α2C2-β2E2-b)

(8)

f34=yf3+(1-y)f4

(9)

由上述式(6)、式(9)可得时间敏感度强、弱的复制动态方程分别为F1(x,y)和F2(x,y)。

F1(x,y)=x(1-x)(-2ay+A1-T1-α1C1-

β1E1-A2+T2+β2E2+α2C2+a)

F2(x,y)=y(1-y)(-2bx+B1-T1-α1C1-

β1E1-B2+T2+β2E2+α2C2+b)

(10)

利用雅可比矩阵的局部稳定分析法进行分析，该系统的雅可比矩阵[19]为

(11)

矩阵J的行列式为

det|J|=(1-2x)(-2ay+A1-T1-α1C1-

β1E1-A2+T2+β2E2+α2C2+a)·

(1-2y)(-2bx+B1-T1-α1C1-β1E1-

B2+T2+α2C2+β2E2+b)-

y(1-y)2b·x(1-x)2a

(12)

矩阵J的轨迹为

tr(J)=(1-2x)(-2ay+A1-T1-α1C1-

β1E1-A2+T2+β2E2+α2C2+

a)+(1-2y)(-2bx+B1-T1-α1C1-

β1E1-B2+T2+α2C2+β2E2+b)

(13)

在系统复制动态方程(10)中，令F1(x,y)=0,F2(x,y)=0，可以得到局部均衡点O(0,0)，A(1,0)，B(0,1)，C(1,1)，D(x*,y*)，其中博弈双方的鞍点值为

令λ1=A1-T1-α1C1-β1E1-A2+T2+β2E2+α2C2+a，表示时间敏感度弱的出行者选择轨道交通出行时，时间敏感度强的出行者选择常规公交、轨道交通的收益差值。

令λ2=B1-T1-α1C1-β1E1-B2+T2+β2E2+α2C2+b，表示时间敏感度强的出行者选择轨道交通出行时，时间敏感度弱的出行者选择常规公交、轨道交通的收益差值。

令λ3=B1-T1-α1C1-β1E1-B2+T2+β2E2+α2C2-b，表示为时间敏感度强出行者选择常规公交出行时，时间敏感度弱的出行者选择常规公交与轨道交通的收益差值。

令λ4=A1-T1-α1C1-β1E1-A2+T2+β2E2+α2C2-a，表示为时间敏感度弱出行者选择常规公交出行时，时间敏感度强的出行者选择常规公交与轨道交通的收益差值。

根据博弈演化理论，满足det|J|>0,tr(J)<0的均衡点为系统演化稳定点(ESS),针对不同情形下的参数对博弈演化策略进行讨论，上面共有4个参数，每个参数都存在正负的可能，这样共有16种情形，每种情形都要根据λ的值判断该情形下演化是否稳定。仔细分析参数后发现λ1-λ4=2a，λ2-λ3=3b，即λ1>λ4，λ2>λ3，这样便能剔除掉λ1<0,λ4>0 或λ2<0,λ3>0情形下的7种组合，分别为

1)λ1<0,λ2<0,λ3<0,λ4<0;

2)λ1<0,λ2<0,λ3>0,λ4<0;

3)λ1<0,λ2<0,λ3>0,λ4>0;

4)λ1<0,λ2>0,λ3<0,λ4>0;

5)λ1<0,λ2>0,λ3>0,λ4>0;

6)λ1>0,λ2<0,λ3>0,λ4<0;

7)λ1>0,λ2<0,λ3>0,λ4>0。

下面讨论另外9种符合意义的参数条件下5个均衡点的演化博弈情形。用含参表达式来代表各个均衡点的行列式，结果如表3所示。

表3 均衡点数值带入结果

下面根据表3结果由λi的正、负情形分别讨论以下9种情形的分析结果。

情形1：λ1>0,λ2>0,λ3>0,λ4>0。此时易得仅在均衡点C(1,1)处，有det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{常规公交，常规公交}，即时间敏感度强出行者选择常规公交出行，时间敏感度弱出行者选择常规公交出行。

情形2：λ1<0,λ2>0,λ3<0,λ4<0。此时易得仅在均衡点B(0,1)处，有det|J|>0,tr(J)<0，即该点为ESS,对应的演化稳定策略为{轨道交通，常规公交}，即时间敏感度强出行者选择轨道交通出行，时间敏感度弱出行者选择常规公交出行。

情形3：λ1<0,λ2>0,λ3>0,λ4<0。此时易得仅在均衡点B(0,1)处，有det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{轨道交通，常规公交}，即时间敏感度强出行者选择轨道交通出行，时间敏感度弱出行者选择常规公交出行。

情形4：λ1>0,λ2<0,λ3<0,λ4<0。此时易得仅在均衡点A(1,0)处，有det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{常规公交，轨道交通}，即时间敏感度强出行者选择常规公交出行，时间敏感度弱出行者选择轨道交通出行。

情形5：λ1>0,λ2<0,λ3<0,λ4>0。此时易得仅在均衡点A(1,0)处，有det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{常规公交，轨道交通}，即时间敏感度强出行者选择常规公交出行，时间敏感度弱出行者选择轨道交通出行。

情形6：λ1>0,λ2>0,λ3<0,λ4<0。此时易得在A(1,0)、B(0,1)两点处有det|J|>0,tr(J)<0，则这两点均为ESS，对应的演化稳定策略为{常规公交，轨道交通}和{轨道交通，常规公交}。其演化如图2所示，可知此时当初始状态为O(0,0)时，即时间敏感度强、弱双方都选择常规公交时，双方的出行收益最小，此时双方会有改变策略的强烈动机，尤其是时间敏感度强的一方，最终会演化博弈至A(1,0)、B(0,1)，进一步解释为当时间敏感度强出行者选择常规公交时，时间敏感度弱出行者会选择轨道交通，即演化为A(1,0)，反之演化为B(0,1)。当初始状态为C(1,1)时，即两类出行者都选择轨道交通出行时，会因为交通状况以及因两者选择同一种交通方式造成的损失等因素而改变演化策略，同样会演化稳定至A(1,0)、B(0,1)。

图2 情形6动态演化相位

情形7：λ1>0,λ2>0,λ3<0,λ4>0。此时易得仅在均衡点A(1,0)处，有det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{常规公交，轨道交通}，即时间敏感度强出行者选择常规公交出行，时间敏感度弱出行者选择轨道交通出行。

情形8：λ1>0,λ2>0,λ3>0,λ4<0。此时易得仅在均衡点B(0,1)处，有det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{轨道交通，常规公交}，即时间敏感度强出行者选择轨道交通出行，时间敏感度弱出行者选择常规公交出行。

情形9：λ1<0,λ2<0,λ3<0,λ4<0。此时易得仅在O(0,0)处，det|J|>0,tr(J)<0，即该点为ESS，对应的演化稳定策略为{轨道交通，轨道交通}，即时间敏感度强、弱出行者都选择轨道交通出行。

以上9种演化情形的均衡点稳定性分析如表4所示。

表4 均衡点稳定性分析

3 参数讨论

在上述构建的博弈模型中，从λi的表达式来看，有11个参数的变动会引起λi的正负变化，这会造成不同策略的转变，考虑到αi、βi(时间价值系数)和Ci(舒适度系数)当模型构建完成后为定值，故以下仅考虑其他6种参数的变化所带来的影响。

由表5可看出A1的增大会引起λ1、λ4的增大，A2增大会引起λ1、λ4的减小，又因为λ1>λ4，若最初情形为1，故适当增加A2的值会引起情形1向情形8的转移；B1的增大会引起λ2、λ3的增大，B2的增大会引起λ2、λ3的减小，同理λ2>λ3，适当增大B2会引起情形1向情形7的转移；a增加会引起λ1增大、λ4的减小，若最初情形为9，增加a的值会引起情形9向情形7的转移，b的增大则会引起λ2的增加、λ4的减小，故增大b的值会引起情形9向情形2的转移；而E1和T1的增大则会同时引起λi的减小，E2和T2的增大则会同时引起λi的增大，同样增大或减小其值也会引起不同情形下的转移。

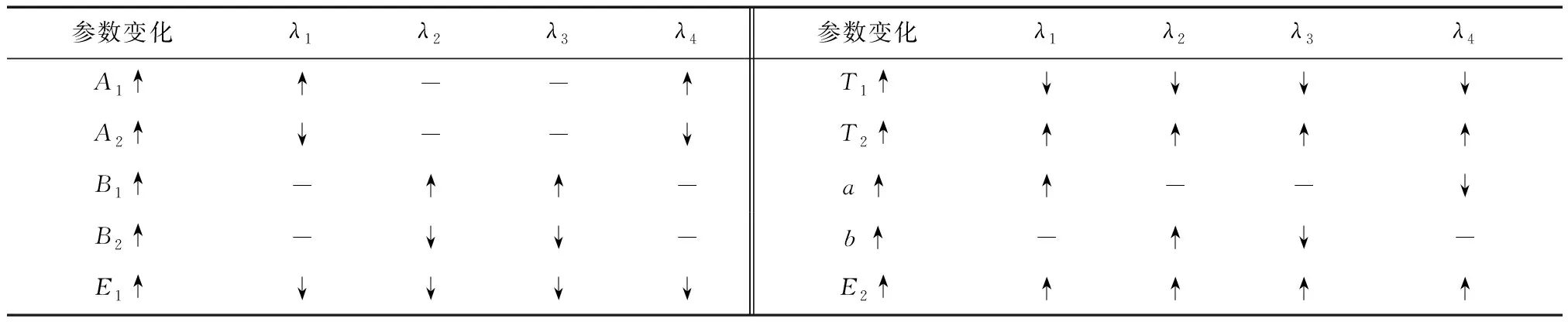
表5 参数变化对λi的影响

4 数值仿真分析

某市区公共交通主要分地铁和公交两大类，居民出行时主要选择地铁X和公交Y线路。简化路线拓扑如图3所示。通过对该地区进行实地调研，并通过问卷形式对居民的出行选择进行调查，选定第一组数据整理计算后得到的相关模型参数如表6所示(表中数据单位已标准化)。

图3 某市路线拓扑

表6 参数值

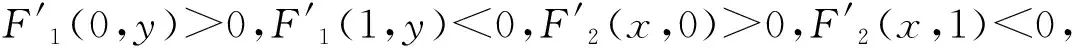
图4 不同时间敏感度出行者动态演化数值变化

图5 双方策略选择概率演化曲线

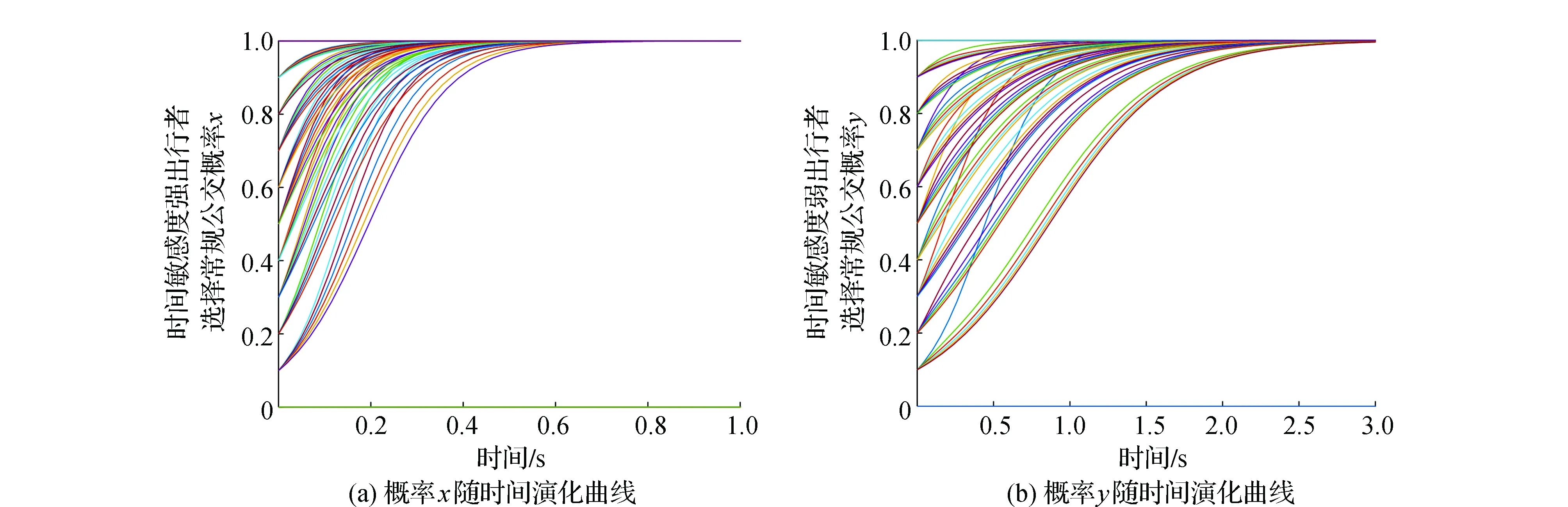
图6 概率x、y动态演化

下面探究在其他条件不变的情况下a值的不同对演化的影响。由λi的表达式可看出a值仅影响λ1,λ4的正负，当a值不断增大，即不同时间敏感度出行者选择常规公交出行方式时给时间敏感度强出行者造成损失增大时，会使λ1值增大，λ4值减小，当λ1>0,λ4<0时，情形1会向情形8演化，即最终演化结果会趋向于B(0,1)，策略集为{轨道交通,常规公交}，故在满足情形1的情况下a的大小仅仅影响x的走向，对y无影响，其中x随a的变化如图7所示。由图7可看出，当a较小时，x演化总趋向于1，当a增大到一定程度时，x会逐渐趋向于0。反映到实际情况时，常规公交、轨道交通都是城市公共交通的重要组成部分，两者在承担城市居民出行时，扮演着相互协作的作用。当两类出行者选择常规公交的比例较大时，会给时间敏感度强出行者造成较大损失，蒙受损失较大一方便会寻求轨道交通作为出行方式，故图7的演化结果与实际情况相符，这也很好印证了轨道交通在城市公共交通中扮演的作用。随着地面交通压力的不断增大，交通延误不断增加，而轨道交通则起到了缓解这一交通问题的作用。

选定第二组测试数据A1=120,A2=105，B1=100,B2=83，a=8,b=5，其他参数同上。此情形下计算出的λ1>0,λ2>0,λ3<0,λ4<0，对应情形6。

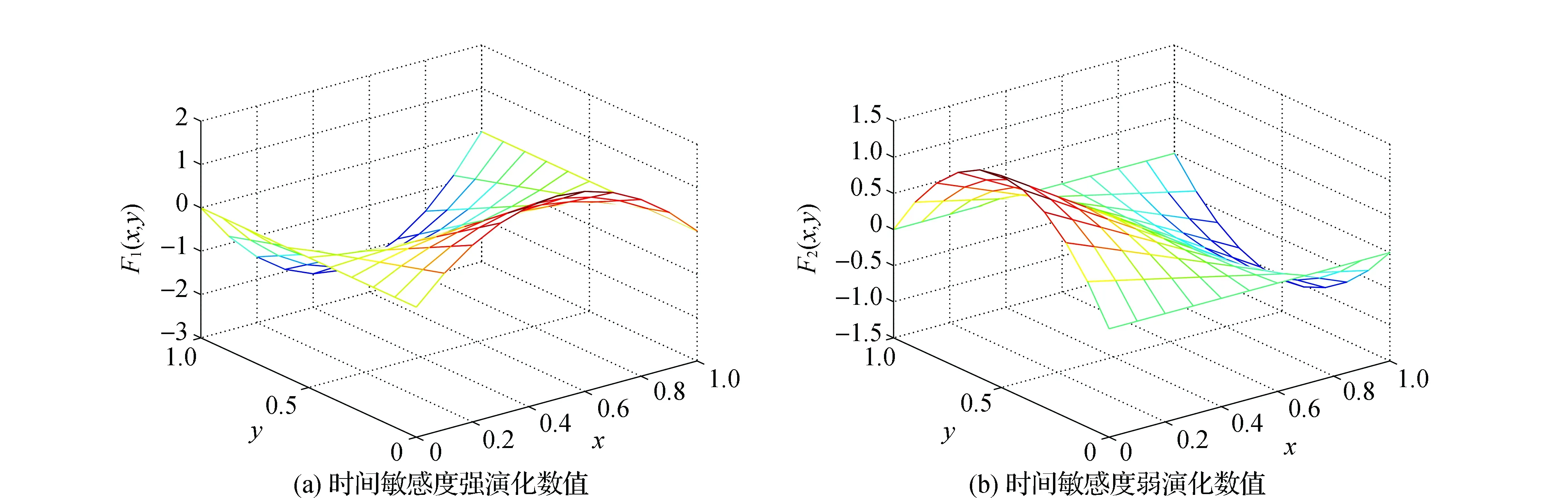
图8 不同时间敏感度出行者动态演化数值变化

图9 双方策略选择概率演化

5 结论与启示

根据出行者对出行时间敏感度的不同建立了演化博弈模型，以出行者出行收益为基础结合出行成本建立了博弈收益函数，同时考虑了在计算道路交通的通行时间时，引入了BPR道路阻抗函数，更加合理地计算了通行时间，重点研究了对时间敏感强、弱双方的策略选择问题。

1)演化博弈的过程根据参数的正负可以划分为9种不同情形，其中有4种情形的演化策略为{常规公交，轨道交通}，有4种情形的演化策略为{轨道交通，常规公交}，有1种情形的演化策略为{常规公交，常规公交}，有1种情形的演化策略为{轨道交通，轨道交通}。

2)在该博弈模型中共涉及到10个参数，除去时间敏感度系数、舒适度系数，其它参数的增大或减小会引起不同情形间的转移，即会引起博弈双方向不同策略转化。在数值分析部分模拟了随着时间敏感度强的收益损失a的增大，其演化方向会随之向另一方转化，即由策略{常规公交，常规公交}向{轨道交通，常规公交}的策略转化。

3)常规公交、轨道交通作为城市公共交通的重要组成部分，相关部门在规划设计时更要合理分配资源。交通规划部门通过适当疏通地面交通减小延误、提高行车准点率、合理规划常规交通和轨道交通的线路走向等措施便能最大限度地使交通资源得到充分利用。同时，由上述模型也能看出，当两种公共交通方式出行收益一定时，车票的变化也会对演化博弈走向产生影响。相关部门在进行交通运输规划与管理时，要综合、全面考虑影响出行的各因素，做好调研，合理做出预判，且要根据实际交通状况做出调整，以保证交通顺畅运行。