基于Savitzky-Golay算法的某深基坑监测数据降噪处理

黄明辉，李梦云，代 煜

（1.周口职业技术学院建筑工程学院，河南 周口 466000；2.江西省机场集团有限公司，江西 南昌 330114；3.河南科技职业大学建筑工程学院，河南 周口 466000）

在基坑工程监测过程中，影响工程监测数据的外部因素较多[1]，导致工程监测数据易受外界因素及监测设备自身误差而表现出明显离散特性，引起监测时程曲线呈现一定的随机波动特点[2-3]，短时间段内影响工程人员对基坑支护稳定性的准确判断.

为提高工程监测精度与监测结果的准确性，近年来已有较多理论方法，例如RS-MIV-ELM模型[4]、神经网络法[5]、灰色理论法[6]等被运用到基坑工程的监测数据处理中，且都获得了较为理想的分析效果.然而此类分析方法多集中于对监测数据的预测，未能对初始的监测时程曲线进行修正和降噪处理.为提高工程数据的可视化程度，并短期内预估基坑支护结构与岩土体变形发展趋势，本文运用Savitzky-Golay算法对基坑实时监测数据进行平滑降噪处理，可为提高工程监测数据的可视化程度及基坑变形走势观察提供参考.

1 工程概况

本项目为南昌地区某地铁车站基坑工程，基坑设计深度约16.6～18.3 m，工程整体采用地下连续墙联合三道内支撑体系的支护形式.为实时掌控基坑开挖支护的稳定性，监测项目紧紧围绕支挡结构、基坑临近岩土体与周边环境安全几个方面展开，并针对性的对地下连续墙顶部侧移、连续墙身变形、内支撑轴力增长及基坑外部地下水位变化等几个项目展开长时间监测.本项目基坑工程支护设计平面与测点分布如图1所示.

图1 基坑监测点平面布置

2 最小二乘法滤波应用

2.1 监测数据预处理

在基坑工程建设施工过程中，根据围护结构的实时动态可直接反馈得到工程项目的稳定性与否.为探析基坑稳定性随时间的变化趋势，选取图2所示地下连续墙顶部某处测点的采集数据展开分析.根据此测点处连续墙顶部侧向变形的折线走势来看，基坑支护结构变形虽随着时间推移大体呈现先增长后稳定的趋势，但短时间内测点所反映的墙顶变形幅度跳动过大，尤其在基坑施工前期测点数据出现明显的震荡往复轨迹，难以准确判断出短时间内基坑支护的稳定性趋势，需要对监测曲线进行合理处理以得到有效的监测结果.

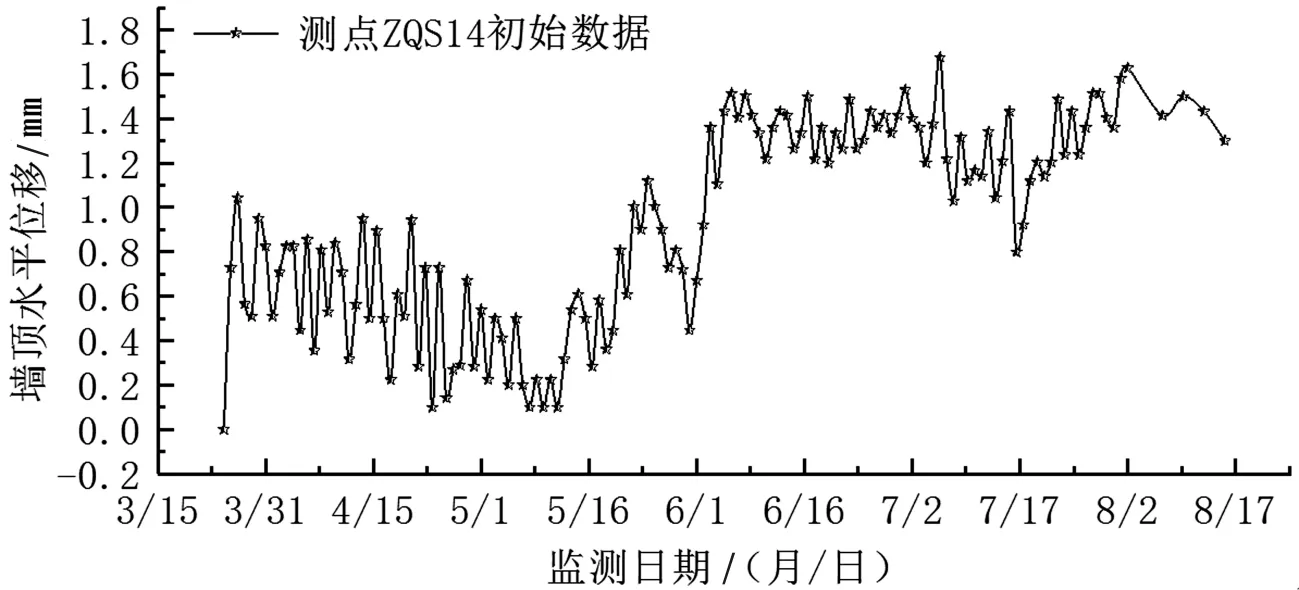
图2 连续墙顶部ZQS14测点处水平位移

受基坑监测技术及外部因素影响，基坑工程监测结果中难以避免地会出现一些误差信息[7]，为消除监测数据中的误差信息，许多学者进行过相关研究并得到有效方法以解决实测数据的降噪需求，例如最小二乘多项式法、小波去噪法、回归分析法等[8-10].因最小二乘多项式法对实测数据的降噪处理准确有效并可以较大程度上保留数据的原始特征，故借助于数据分析软件origin并运用最小二乘多项式法中经典的Savitzky-Golay滤波算法对比LOWESS法、FFT法[11-13]对本项目基坑实时监测数据进行降噪处理，针对不同方法下的降噪处理结果展开进一步分析.在三种不同滤波算法下，连续墙顶部侧向变形的时程变化趋势如图3所示.

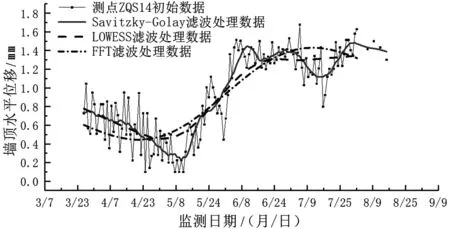
图3 连续墙顶部ZQS14测点处水平位移降噪数据

由图3中初始数据及3种不同滤波算法下的监测曲线趋势可知，经过监测数据的平滑降噪处理，基坑支护结构监测时程曲线的可观性呈现明显提升.根据平滑处理后的数据曲线，可清晰地判断出地下连续墙顶部随时间变化的侧向位移走势.3种滤波算法均在很大程度上筛除了原始数据中的误差信息与数据奇异点，且处理后的曲线走势与初始数据大体无误，尤其Savitzky-Golay平滑滤波算法有效地保留了监测数据中的有效信息，其校正曲线与原数据基本吻合.而LOWESS、FFT滤波算法在本项目基坑数据的降噪处理中却存在一定程度误差，其校正效果明显弱于Savitzky-Golay平滑滤波算法.文献[14]指明，Savitzky-Golay算法优势在于可以较大程度地消除数据噪声，且保证信号形状、宽度不变.该滤波算法在本项目基坑监测中符合数据处理要求，具有较好的实用性，故选用此种数据平滑降噪算法对本工程其他监测项目数据进行预处理分析.

2.2 校正数据相关性分析

虽然经过平滑降噪后的监测数据可视化效果明显提高，并有助于判断现阶段基坑稳定性状态、有助于预估未来短时间内基坑发展趋势，但校正数据的可靠性却是工程数据优化分析的前提和保障.由于校正后的数据与初始数据的相关性可能存在一定程度的误差，若校正数据与原始数据相关性较差，则不能表明此方法在监测数据预处理中的优越性.在处理基坑监测数据的过程中，应合理预判基坑支护结构及邻近岩土体的变形趋势，剔除因各类技术和自然误差而产生的奇异样本，并及时调整滤波的多项式阶次与平滑窗口宽度，以使得校正后的数据适配于初始数据样本，达到对工程监测数据优化处理的目的.

为验明Savitzky-Golay滤波算法在监测数据处理中的有效性与失真程度，将校正前后的各时间点监测数据进行表1所示对比分析，并对校正前后的监测数据进行图4所示线性拟合，分析监测数据在降噪前后的实际相关性.

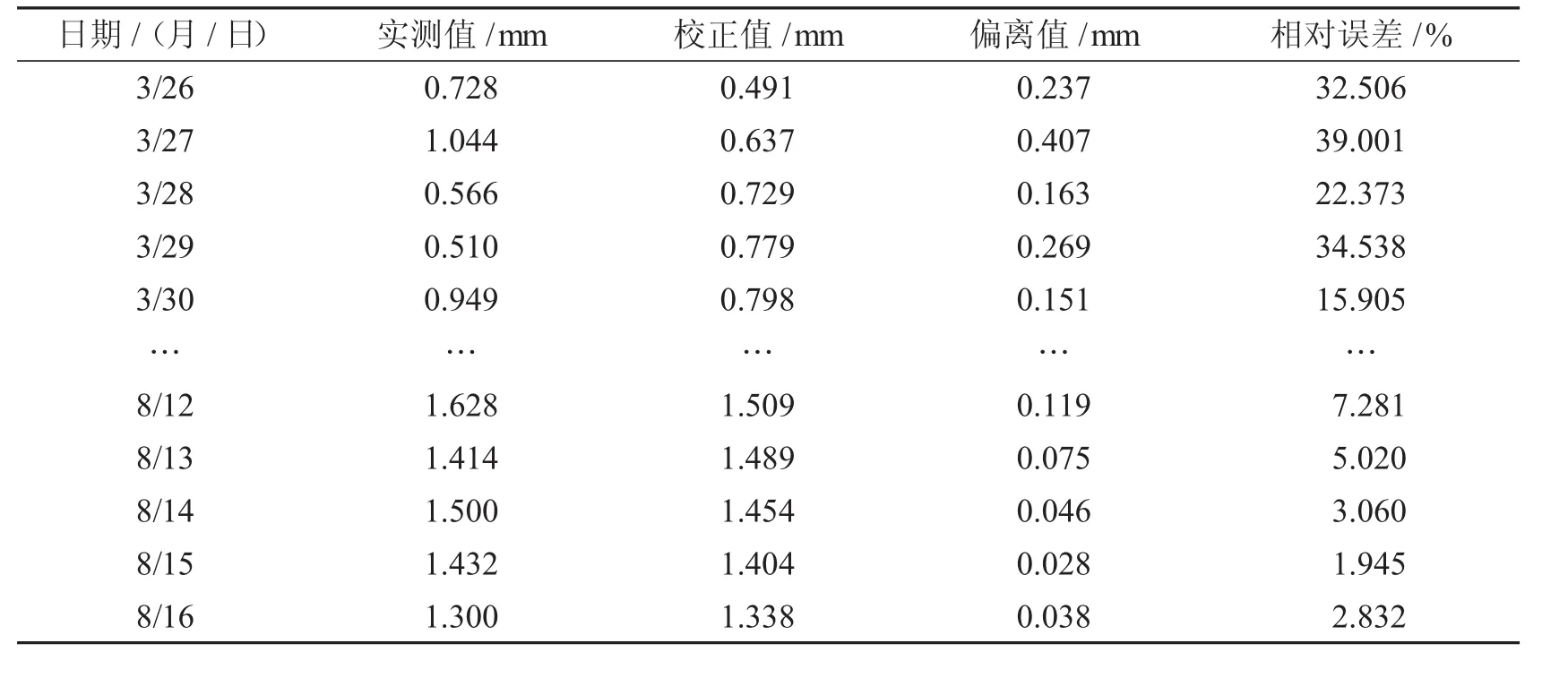
表1 监测数据降噪处理前后对比

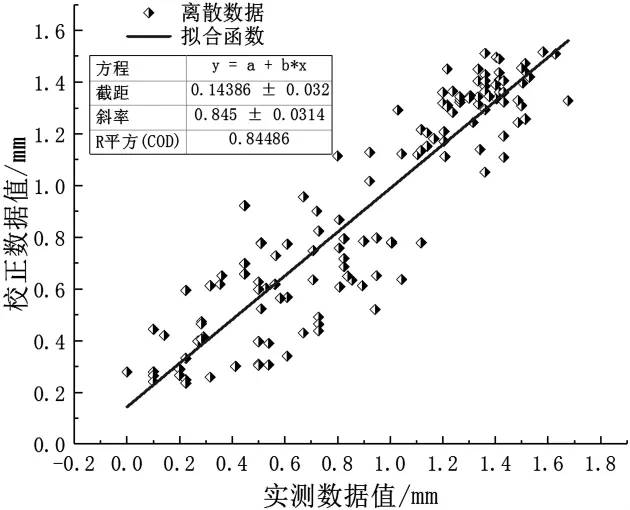
图4 实测数据与降噪数据拟合精度示意

由校正前后的监测数据对比情况判断，因基坑工程在施工初期监测初始数据出现明显震荡、往复情况，导致降噪后的数据在工程初期与初始样本存在一定程度的偏差，图中用来表示相关程度的监测数据点在拟合函数线附近分散排布，并且文献[15]研究结果表明，在数据校正的开始阶段，供滤波算法分析的初始数据样本数量较少，导致计算系统难以精准捕捉工程监测数据的变化规律，但校正值与实测值在初期的相对误差可经过人工赋值等方法来解决，对实际应用并无影响.直至工程监测后期，随着供滤波算法分析的初始数据样本数量不断增加，基坑监测的校正数据和初始数据样本的相关性不断提升，基坑平滑降噪的精度持续增长，后期工程监测数据在降噪前后误差范围已降低至3%范围内.

为量化校正前后工程数据的相关性，采用线性回归的相关指数R2（R-squared）[16]展开分析.设定基坑工程中监测数值的初始值为yi；基坑监测数据的平均值为，即为拟合函数的预测值.则可得公式1所示关系式：

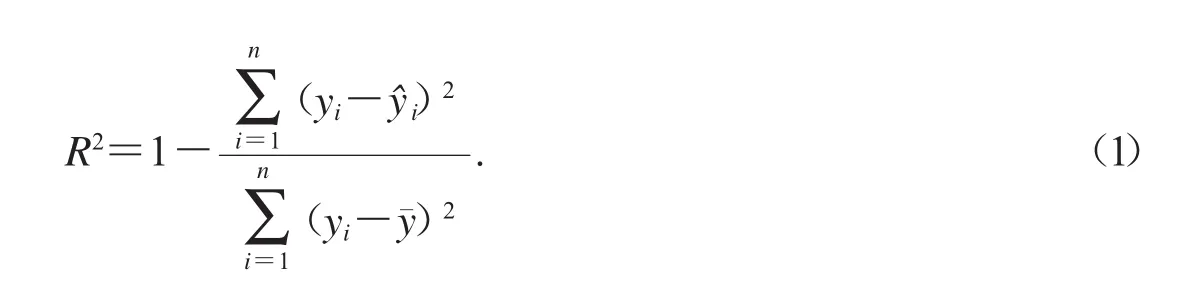
因R2值位于[0，1]的区间范围内，其数值越接近于1，则表明回归效果越好，校正数据的关联性越强.当相关指数R2达到0.800时，研究对象的数学模型即拥有理想的拟合优度.而本工程监测数据经平滑降噪后，线性回归指数R2已达到0.845.由此可判断采用Savitzky-Golay滤波算法剔除了监测数据误差信息的同时，很大程度的保留了数据的有效内容，其校正结果可为基坑安全状态把握提供较好的辅助和预测作用.

3 基于Savitzky-Golay算法的监测数据分析

3.1 墙顶水平位移分析

连续墙顶部水平位移是轨道交通工程监测中一项关键的项目指标，其数值大小与变化的趋势可直接表征支护结构上部空间与地面周围岩土体支护的稳定性.为验证Savitzky-Golay滤波算法在工程监测项目中的适用性，在图5所示基坑支护标准段与端头井段内各提取一个测点，针对该部位监测数据展开优化处理与工程稳定分析.

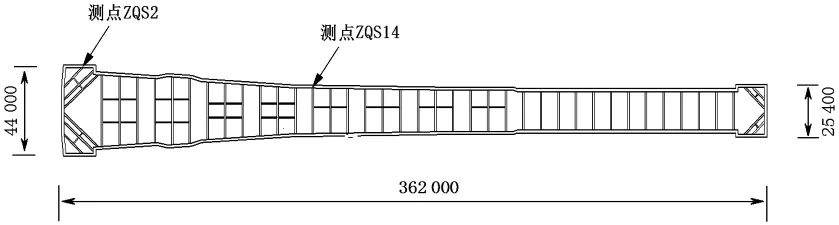
图5 连续墙顶部水平位移监测点平面布置示意

经基坑工程监测数据的降噪处理后，可得两处测点的时程曲线如图6所示.根据校正后的监测曲线走势可知，随着工程场地内土方持续开挖，基坑水平方向土体应力不断释放，改变了地下连续墙初始的平衡状态，其顶部朝向基坑内侧不断产生侧向变形.尽管施工过程中按规范要求及时搭建了水平内支撑，但因土方卸荷产生的土压力差值较大，而内支撑在水平向约束能力有限，导致连续墙顶部侧向位移在施工前中期持续产生较大程度增长，随着基坑开挖至设计深度并浇筑建筑底板，连续墙顶部侧移情况方逐渐趋于稳定.

图6 墙连续墙顶部水平位移时程变化曲线

对比所选取的两个典型位置处的墙顶侧移情况分析可知，端头井ZQS2测点位置处的连续墙变形受相邻短边一侧墙体变形控制程度较大，表现出明显的坑角效应[17]，而标准段ZQS14测点位于长边连续墙跨中位置，短边墙体对该测点位置处墙体影响程度较弱，导致两典型位置处连续墙顶部侧移呈现差异性的增长.

3.2 墙身水平位移分析

工程施工状态下，基坑内部土体不断被卸载移除，连续墙墙身受不断增大的水土压力差作用而逐渐产生不均匀变形.作为评价基坑支护稳定的典型指标之一，连续墙墙身的变形程度可直接代表基坑工程在动态施工下的支护效果.为评估基坑稳定性状态，选取图7所示两典型位置处的监测数据展开优化分析.

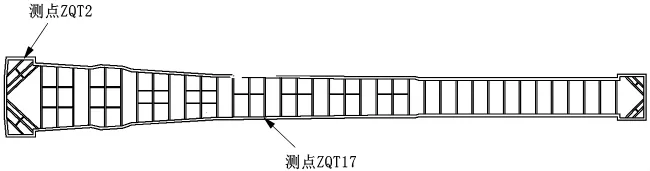
图7 连续墙墙身水平位移监测点平面布置示意

针对工程数据离散性的特点，运用Savitzky-Golay滤波算法对初始数据样本进行校正分析，可得图8所示地下连续墙侧移随深度变化的时程曲线图.由图中数据可知，随着工程进度增加，连续墙最大变形区域逐渐往下转移，在土方开挖中后期，连续墙中下部的变形程度远大于上下两端，呈现出明显的“弓形”分布.由于本项目场地基岩埋深较浅，连续墙端部嵌入到高强度的风化岩内，风化岩为连续墙底端提供了较好的约束作用，使得墙端变形程度远小于其他各处.在本项目监测的各时间段内，两测点所采集的墙身最大侧移值均不足18 mm，满足地下连续墙变形在轨道交通工程建设中±30 mm的变形允许值要求.

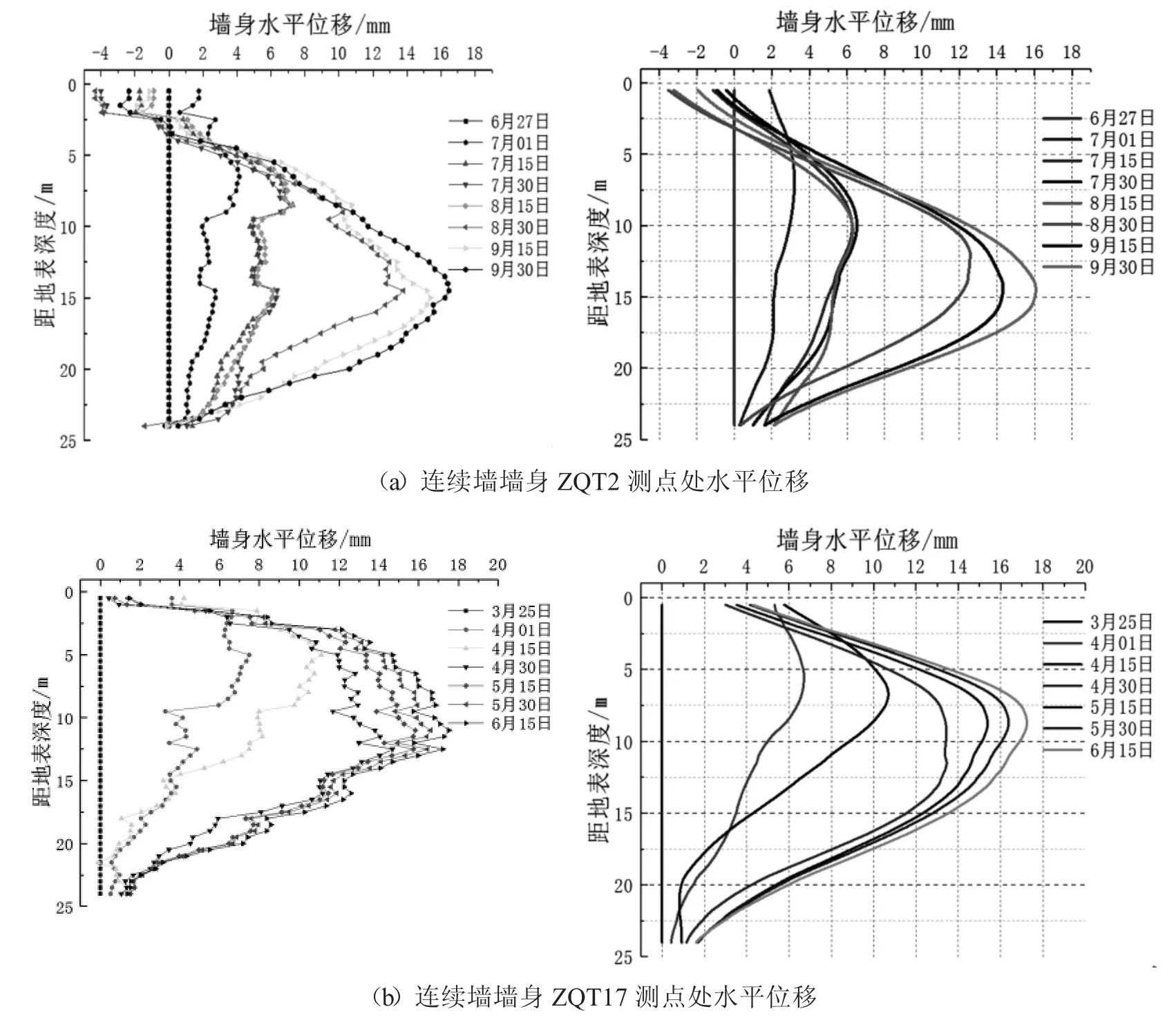
图8 连续墙墙身水平位移时程变化曲线

3.3 内支撑轴力变化分析

在基坑工程中，沿地下连续墙纵深不同位置处搭建水平内支撑有助于抵抗墙身传递而来的侧向水土压力，限制连续墙体产生过大侧向变形，进而保护基坑支护的稳定性，内支撑对控制基坑变形起到重要作用.在本项目基坑工程中，为提升基坑支护性能，沿图9平面所示不同深度处分别布置三道内支撑.

图9 内支撑轴力监测点平面布置示意

随着坑内土方开挖深度增加，连续墙两侧土压力差值不断变化，墙体变形逐渐往中下部转移，导致浅层岩土体与连续墙接触面上土压力减弱[18].若首层内支撑采用钢支撑形式，在连续墙受力位置转移的情况下，可能导致钢支撑产生脱空现象.因此本项目基坑工程中沿首层设置为混凝土支撑，通过将混凝土支撑与连续墙现浇成整体，以增加支护结构整体刚度，并在其下分别灵活布置两道钢支撑，以保证基坑支护的稳定性.

根据图10所示优化后的工程监测时程曲线可知，随着工程进度不断推进，连续墙变形程度增大，由墙体侧移所引起的应力传递给水平内支撑体系，使得内支撑受压而轴力增长.代表三道水平内支撑受压程度的轴力数据均由支撑体系搭建开始逐渐增大而后趋于稳定.在基坑开挖、支护、支撑拆除期间，内支撑轴力始终处于安全预警值范围内，代表本项目内支撑体系在长时间的动态监测下，一直未产生较大变形和内力变化.

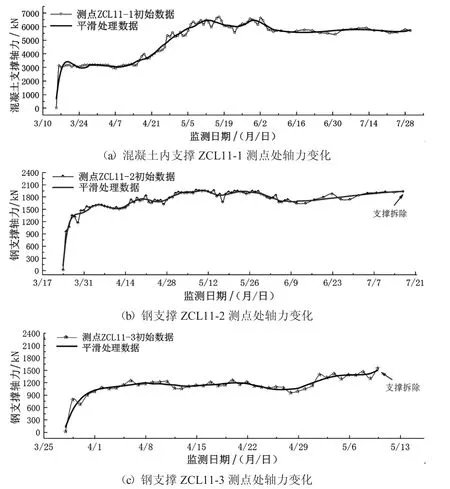
图10 内支撑轴力观测时程变化曲线

3.4 坑外地下水位变化分析

本项目建设场地位于城区范围，地铁车站临近市政道路与建筑物，工程施工对基坑周边地表土体沉降控制要求较高，因此不可进行坑外降水而需要采取坑内降水的形式，降水前将连续墙端部嵌入风化岩内以切断基坑内外侧水力联系，由此减弱降水施工对地表的沉降影响.由基坑工程设计要求，应对坑外周边地下水位进行实时监测，避免工程开挖和降水对地层产生过量的沉降影响.为研究Savitzky-Golay滤波算法在地下水位监测项目中的应用效果，选取图11所示两处测点展开分析.

图11 基坑外部地下水位监测点平面布置示意

由图12所示Savitzky-Golay滤波算法优化后的地下水位走势可知，受气候性降水与工程施工影响，基坑外侧地下水水位在施工期间持续波动，地下水位整体呈现先升高后震荡下行的趋势，在工程施工后期，地下水位较为平稳.由优化数据的时程曲线可判断，若无降雨入渗影响，未来短时间段内基坑外侧地下水位下降深度将持续保持稳定且降深不足0.5 m.在整个基坑工程的建设期间，基坑外部的地下水涨落一直处于正负1 m的警戒区间内，始终保持着正常的水平状态.

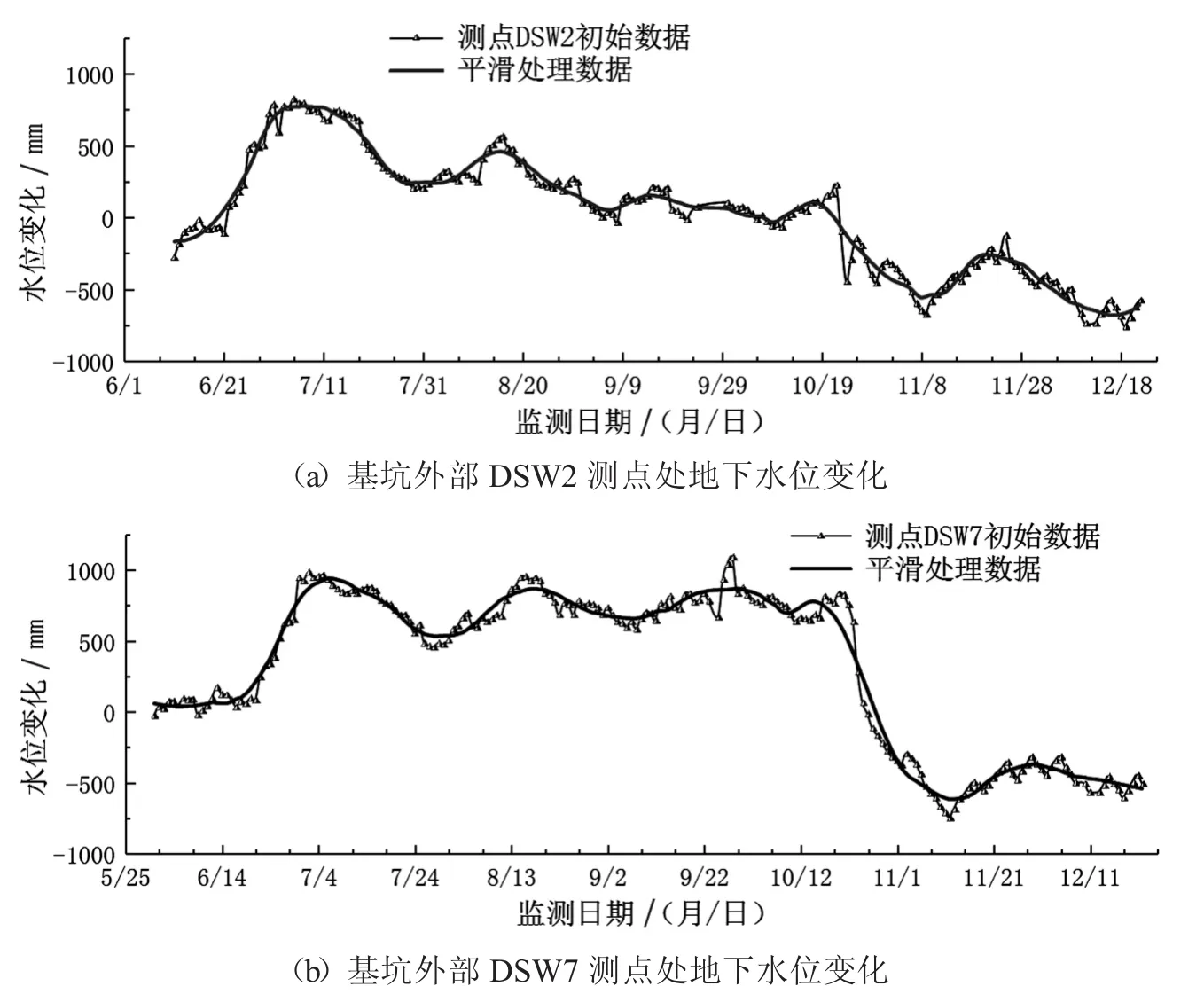
图12 基坑外部地下水位时程变化曲线

4 结语

在本研究范围内可得出以下结论：

1.相比LOWESS和FFT滤波算法，Savitzky-Golay滤波算法能更有效地保留监测数据中的有效信息，其校正曲线与原数据吻合更好.

2.在基坑监测数据的实测值与校正值的拟合函数中，函数线性回归的相关指数R2达0.845，可认为本项目基坑监测数据的降噪平滑曲线与初始数据相关性较强，可为初始数据提供较好的辅助校正作用.