一个基于低通图滤波器的推荐模型

彭裕培，陈 力

（汕头大学工学院电子信息工程系，广东 汕头 515063）

0 引言

推荐系统在现实生活中无处不在，比如淘宝的商品推荐系统、美团的美食推荐系统等，如图1所示.正是由于推荐系统能够创造极大的经济价值，无论是在学术界还是在工业界，相关的研究都层出不穷.总的来说，推荐系统的发展经历了三代技术的改进.第一代推荐系统是基于协同过滤[1]的方法，将与用户明确偏好的商品推荐给用户，在传统推荐系统中使用最广泛，但其未能解决数据稀疏和冷启动问题.第二代推荐系统是基于深度学习模型[2]，通过深度学习技术完成推荐任务，虽然解决了数据稀疏问题，却仍未解决冷启动问题.为了解决冷启动问题，经过不断探索，图结构模型在推荐领域中受到越来越多的青睐.第三代推荐系统是基于图神经网络（GNN）的方法[3]，学习节点、边和子图更深层的特征，预测未观察到的数据从而预测用户未来的行为.

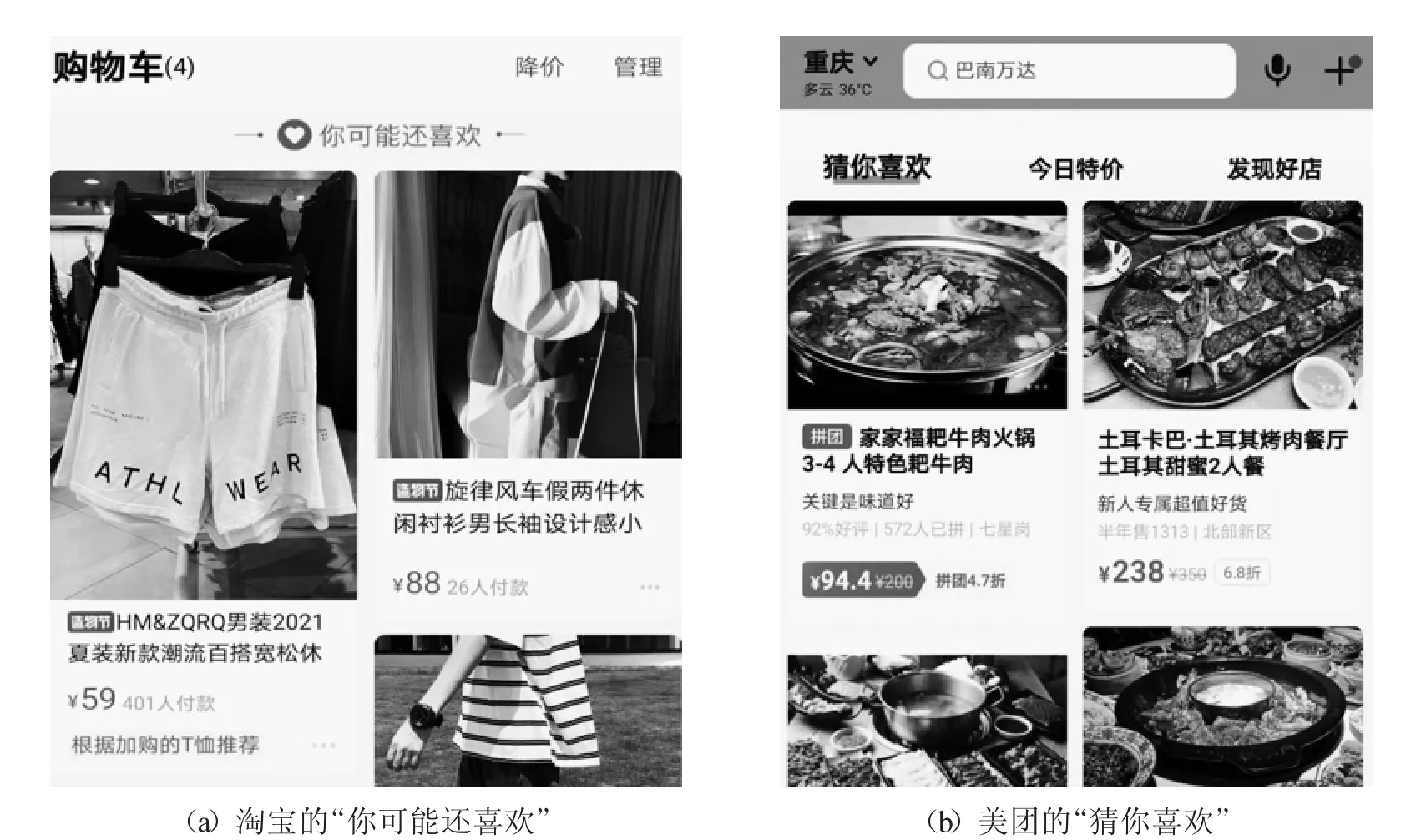
图1 推荐系统实例

近年来，基于图网络的个性化推荐算法越来越流行.起初，Zhou等人对其进行了一系列的研究，并提出基于用户-商品的二分图推荐算法[4].Liu等人通过不对称查询的二分图资源网络的建模，提出了更高精度和覆盖率的二分图推荐模型[5].王国霞等人提出了基于二部图影射的推荐模型[6]，利用随机游走得到图上每个节点的稳定概率，进而衡量用户的兴趣偏好.杨晗等人研究了网络表示学习在推荐系统中的应用[7].Luo等人提出了一个基于NMF的协同过滤模型[8]，对每个特征的非负更新过程进行了一系列研究和讨论，利用基于非负单元素的更新规则，对Tikhonov正则化项进行了集成操作.Rianne van等人提出GCMC算法[9]，通过采用GCN编码器生成用户-商品的表示，其只考虑了最邻近的一阶邻居，因此只有一个图卷积层.Xiang Wang等人提出NGCF算法[10]，将用户-商品的交互信息集成嵌入到二部图结构中，形成了用户-商品图中的高通连接性表达，从而使得协作信号有效地以显示方式编码到嵌入过程中.

然而目前的推荐系统的基本假设是用户对于商品的交互行为是稳定且可信的.事实上，在真实推荐系统中，用户所点击的商品并不一定能够反映其真实偏好，例如某些标题党的诱导点击或者是误点击行为.这种记录下来的反馈数据会极大的影响推荐系统对于用户偏好的学习和估计.在错误样本的情况下，模型的推荐效果会出现大幅度的下降.解决上述问题实际上是非常困难的.要解决上述问题，最简单的方法就是对数据进行预处理如噪音的过滤和特征的抽取，但是这些并非是端到端的方法，无法针对最后的推荐任务进行端到端的优化；另一方面基于学习的方法如引入注意力机制[11]，传统方法如引入注意力机制的邻居，学习过程可以一定程度的缓解噪音连接，但是其需要引入大量的计算复杂度.

综合考虑上述分析，为了实现噪音交互的过滤并实现一个高效推荐系统，需要解决如下的三个挑战：（1）如何设计实现对高频噪音连接的有效过滤.二部图上的交互信号实际上包含稳定的低频信号和波动较大的高频信号，那么如何对这些高频信号和低频信号进行有效过滤是一个迫切需要解决的问题.（2）如何对高阶交互中所蕴含的不同层次的噪音连接进行过滤.通常来说推荐系统为了解决稀疏和冷启动的问题，会考虑用户商品交互中的高阶连接.但是，这也给噪音连接过滤问题带来了进一步的挑战.在高阶连接中如何对不同阶邻居的信息进行过滤和筛选是一个开放式的问题.（3）在过滤噪声之后，如何学习稳定的用户和商品表示并实现推荐.高效准确的估计用户的复杂偏好是推荐系统的基本需求.一个好的偏好学习模型可以极大的提升后续推荐任务的效果.

图信号处理[12-13]技术为人们处理不规则域的高维数据提供了一个新型有效的工具.2013年Shuman等[12]将图的节点上的特征定义为图信号，从传统信号处理角度在图论基础上提出了“图信号处理”的概念，并定义了图傅里叶变换、图滤波、图卷积等概念.图上不同频率的信号均可以通过图信号处理技术进行分析和处理.当节点与其邻居的特征较为接近时，即通过边所连接的节点变化幅度较小时，这反映为一种变化幅度较低的低频信号.反之，如果变化幅度较大，则反映为一种高频信号.具体的，用户-商品交互图中，如果用户总是点击其喜好的商品，交互行为反映为变化较小的低频信号.如果用户误点击一些其不喜欢的商品，那么就反映为图上的高频信号.例如图2中三个用户均喜欢电子产品，偏好相似，为低频信号.但是，其中一个用户误点击了一双鞋子，该噪音连接会引入高频信号.可以看出，低频交互信号更好的反映用户偏好，而高频交互信号的作用较小.

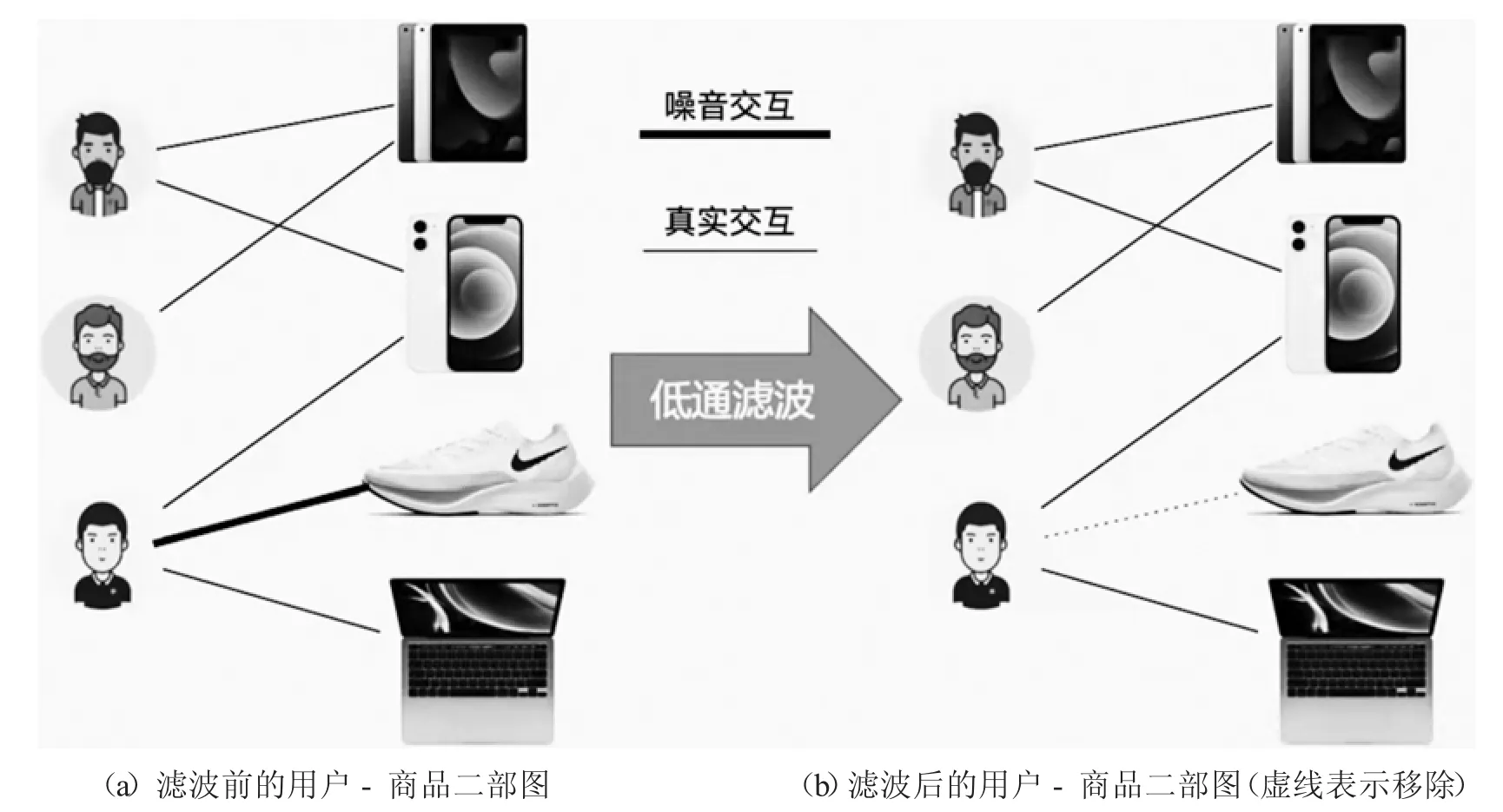
图2 低通滤波前后的用户-商品二部图

本文研究了用户-商品二部交互图上的噪音连接问题，并设计了一种低通图滤波器，来对用户-商品交互进行过滤和降噪，并学习鲁棒的用户表示进而提升后续所推荐任务的效果.具体来说，我们从图信号处理中的谱图理论出发，将用户和商品定义为顶点，其特征定义为图信号，用户和商品的交互关系定义为边，分析了图滤波器对于交互信号的过滤作用.然后，设计了一种低通图滤波器，其可以有效抑制图上的高频信号，并筛选出稳定的低频信号.进一步的，我们将其扩展为K阶图低通滤波器，来过滤K阶邻居中的噪音连接.通过上述图滤波器所学习的用户偏好和表示，我们设计了LGFRec模型，其可以有效地为用户推荐其感兴趣的商品.在两个公开数据集上的大量实验验证了我们所设计的模型的有效性.

本文的组织如下：第一部分为理论模型，说明了图信号处理相关理论和本文模型的建立；第二部分通过实验对本文方法进行评估；第三部分为本文做出总结.

1 理论模型

通常来说，用户的偏好或者商品的特性都是相对稳定的.例如，一个电子产品爱好者所点击的商品大部分为电子产品，这种交互可以精准的反映用户的偏好.但是，偶尔由于用户误触的点击行为或者是“标题党”等现象，会造成一些噪音链接，即推荐系统所记录和观测到的用户-商品交互是有噪音的[14].为了精准预测用户-商品的点击行为，我们希望去除高频信号的噪音，保留低频且稳定的信号来学习用户和商品表示并进行推荐.为了实现上述目标，本文从设计的一个二部图上的低通滤波器来保留用户稳定的偏好，即低频信号，获得一个基于低通图滤波器的推荐模型（Recommendation with Low-pass Graph Filters，LGFRec）.接下来，将会首先介绍用户-商品二部图的构建过程，低通图滤波器的设计，以及如何进行推荐结果的预测.

1.1 数据构建

本小节首先介绍数据集的构建部分，即：如何将用户-商品交互建模为图，方便进一步从图信号处理的角度来实现推荐.具体来说，二部图＝（v，ε，x）建模了用户与商品的历史交互过程.这里为了方便，将用户和商品节点进行统一处理.节点集合v＝{v1，v2，…，vn}表示用户与商品的节点集合，共计n个.x＝[x1，x2，…，xn]T∈Rn×d，表示节点的特征，xn∈Rd代表节点的vn初始特征，边集合ε表示用户与商品的历史交互信息，如图3（n＝7）所示.

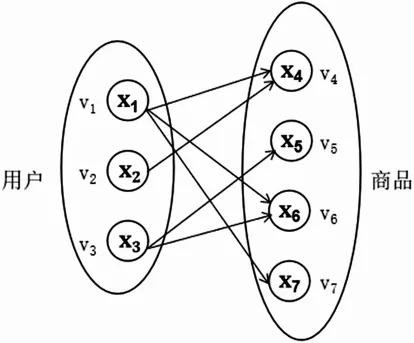
图3 用户-商品交互的二部图（n＝7）

用户与商品的历史交互，可以进一步转为如下交互图邻接矩阵A∈Rn×n：

基于用户和商品是否产生历史交互，我们可以学习和抽取用户对于商品的偏好.若用户vi点击过商品vj（Aij＝1），那么这代表用户vi比较喜欢商品vj.如图3所示的交互图中，用户数为3，商品数为4，其邻接矩阵为

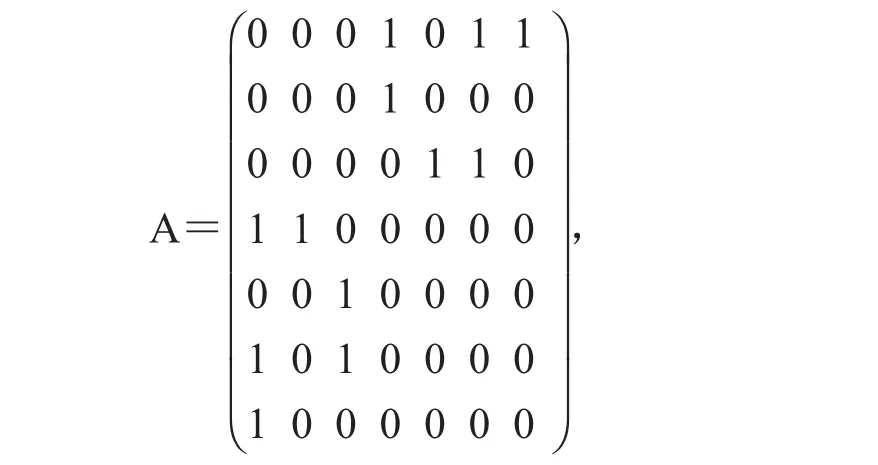
A35＝1，说明用户v3点击过商品v5.

需要注意的是，A中所记录的历史交互是有噪音的.例如，当用户vi误点击或者偶发点击商品vj时，当次点击行为并不真实反映用户的偏好情况.

1.2 图信号及其分解

图信号f是对图上节点的特征的定义，如式（2）所示：

f（v1）表示节点v1上的信号值.

在滤波之前，首先将图信号f分解为一组基的组合[15]，这与经典的傅里叶变化类似.不同节点vi对应不同的频率的信号，这表明每个节点均会对应与其某个特征向量相关的值.同时，图信号f可以分解为特征向量的线性组合：

其中z表示特征向量U的系数，系数zi表示基信号ui的强度.

1.3 图滤波器

为了对历史交互A进行降噪和过滤，过滤高频噪音并保留低频交互信号，本文设计了一个低通图滤波器，其从图信号处理的角度来对用户-商品交互进行降噪和信息筛选.在介绍图上的低通滤波器之前，这里首先引入邻接矩阵、拉普拉斯矩阵、度矩阵、图卷积的概念[11-12].

1.4 低通图滤波器

为了滤除高频噪音并抽取用户稳定的偏好，p（·）需要能够抑制高频信号，保留低频信号.因此，本文将其设计为一个递减的非负线性函数，进而使得G成为一个低通图滤波器.具体来说，低通图滤波器的频响函数如式（10）所示：

1.5 K阶低通图滤波器

进一步地，我们设计了K阶的低通图滤波器，其能够对用户-商品交互图中的K阶交互进行降噪和过滤，即：希望每层图卷积中均可过滤高频噪音，保留低频信号.进一步地，为了增强模型的融合，我们在每一层均加入一个可学习的特征变换矩阵W，如式（13）所示：

其中，Wk代表了第k阶低通图滤波器的权重.通过在推荐系统上应用K阶的低通图滤波器，可以使行为相似的用户具有相似的表示，即所呈现的图信号是平滑的.基于行为相似的用户会选择相似的商品的假设，使用低通图滤波器进行图卷积可以使下游的推荐任务更容易.

1.6 预测模块

基于上述K阶低通滤波器，模型可以在过滤K阶噪音交互的同时来学习用户和商品的表示，其每一行代表一个用户（或者商品）的向量表示并可以准确反映用户（或者商品）的偏好，进而服务于后续的推荐任务.例如，用户vi与商品vj的偏好分别通过向量与来表示，其蕴含了两者图滤波降噪后的特征表示及偏好.

同时考虑用户和商品的特征表示，模型可以预测用户点击商品的概率.具体地，基于用户vi与商品vj向量表示的相似度r^ij，可以预测用户对商品的点击可能性[10、17]，如式（14）所示：

相似的用户或者商品在向量空间的位置会比较接近，这可以通过向量相似度来反映.当用户向量与商品向量乘积越高时（即值越高），表示二者偏好的相似度越高，用户vi越有可能点击商品vj.否则，值偏低.

1.7 损失函数

推荐模型旨在尽可能推荐用户感兴趣的商品，因此，其需要能够判断用户感兴趣的商品与不感兴趣的商品之间差异，如距离的远近.设商品vj'为用户vi不感兴趣商品，相应的点击概率为以贝叶斯个性化排序（Bayesian Personalized Ranking，BPR）损失函数[18]作为优化目标能够满足上述需求：

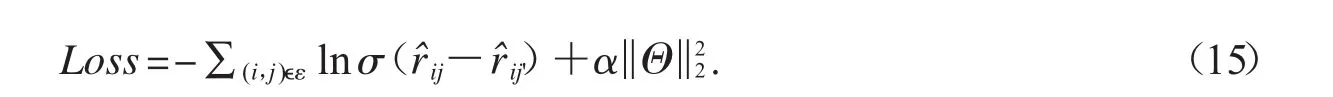
BPR损失函数对数据集中所有样本进行计算，其中（i，j'）可以通过随机负采样得到.为正则项，其约束了LGFRec中可学习参数Θ的大小，防止过拟合.正则项的约束程度与系数α相关.

2 实验

2.1 数据集

为了验证所提出的LGFRec模型的有效性，本文使用了两个公开数据集MovieLens 100k与MovieLens 1M[19]来对其进行实验和评估.数据集具体信息如表1所示.

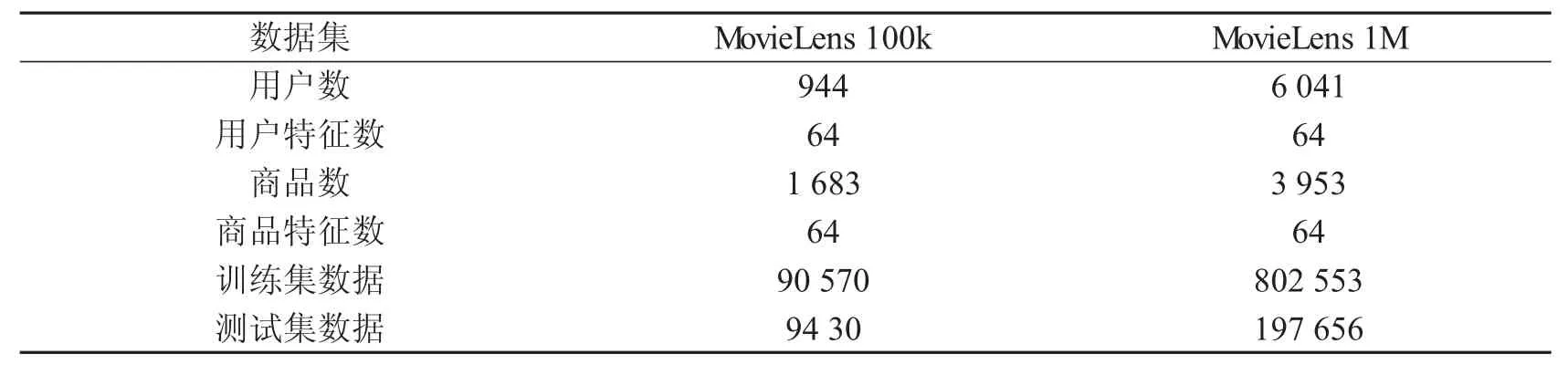
表1 数据集统计信息

对于MovieLens 100k数据集，采用其官方数据划分来进行实验.对于MovieLens 1M数据集，这里对每个用户随机采样20%历史交互商品作为测试数据，其余为训练数据.用户与商品的特征数为64，采用向量嵌入的方式，随着模型进行训练.

2.2 评测指标

对于测试集中的每个用户，本文将用户没有产生历史交互的所有商品均看作负样本.为了验证模型对排序商品的敏感，采用了Top-K的推荐评估方式，利用精准率，召回率，命中率与NDCG这4个指标进行评估，分别写作Precision@K，Recall@K，Hits@K，NDCG@K.

2.3 基准模型

为了证明本文所提出的LGFRec模型的优势，这里将其与几种较新的推荐方法进行了比较：

（1）NMF[18]：这是一种通过BPR损失优化的矩阵分解方法，该方法可以有效学习商品和用户的表示，并基于两者表示的相似度进行推荐.

（2）GCN[20]：这是一种基本的图卷积网络，其通过聚合历史交互信息来编码和学习用户与商品表示，该方法也通过BPR损失优化来进行优化.

（3）GCMC[9]：该模型基于GCN，使用一阶邻域作为特征并且使用多层感知机构建编码用户与商品的关系，进而实现高效的商品推荐.

（4）NGCF[10]：这里是一种基于图神经网络的高阶交互建模推荐模型，其通过编码用户与商品的高阶协同信号来描述用户与商品的表示，从而构建推荐系统模型.

2.4 参数设置

本文采用谷歌开源的深度学习框架Tensorflow来实现模型.在相同数据集中，所有模型均使用相同参数，这样可以确保公平.在搜索最优超参数时，我们尝试了{0.05，0.01，0.005}的学习率，{0，0.1，0.2}的 Dropout，与{10-4，10-5，10-6}的 L2正则化系数.具体参数如表2所示.

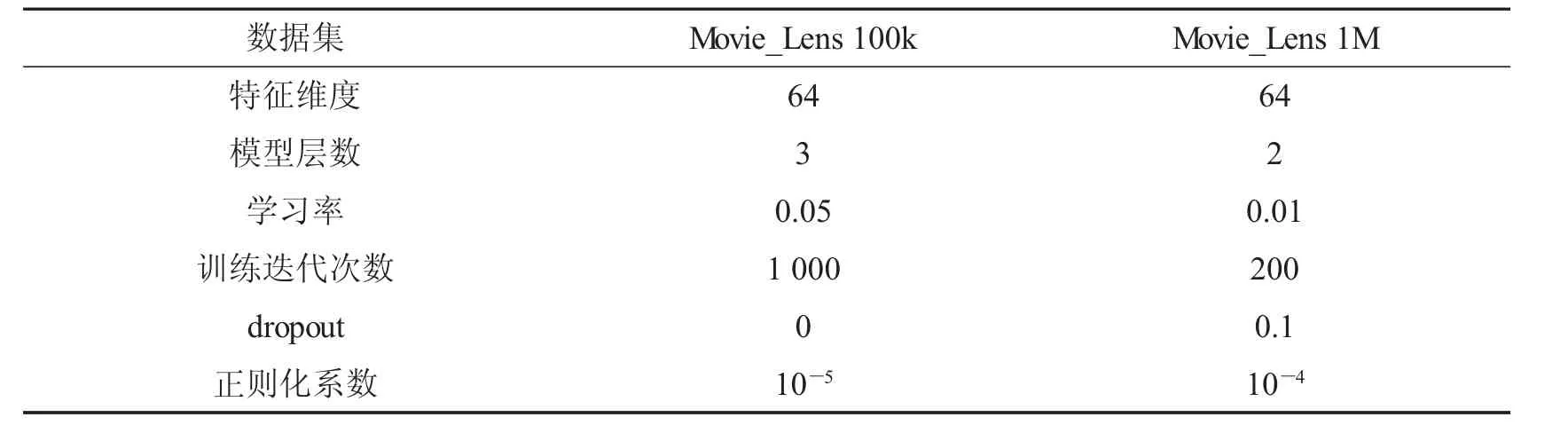
表2 参数设置

2.5 有效性实验

表3展示了不同方法在推荐上的有效性.这里以K＝20为例，来验证我们的LGFRec模型的有效性.

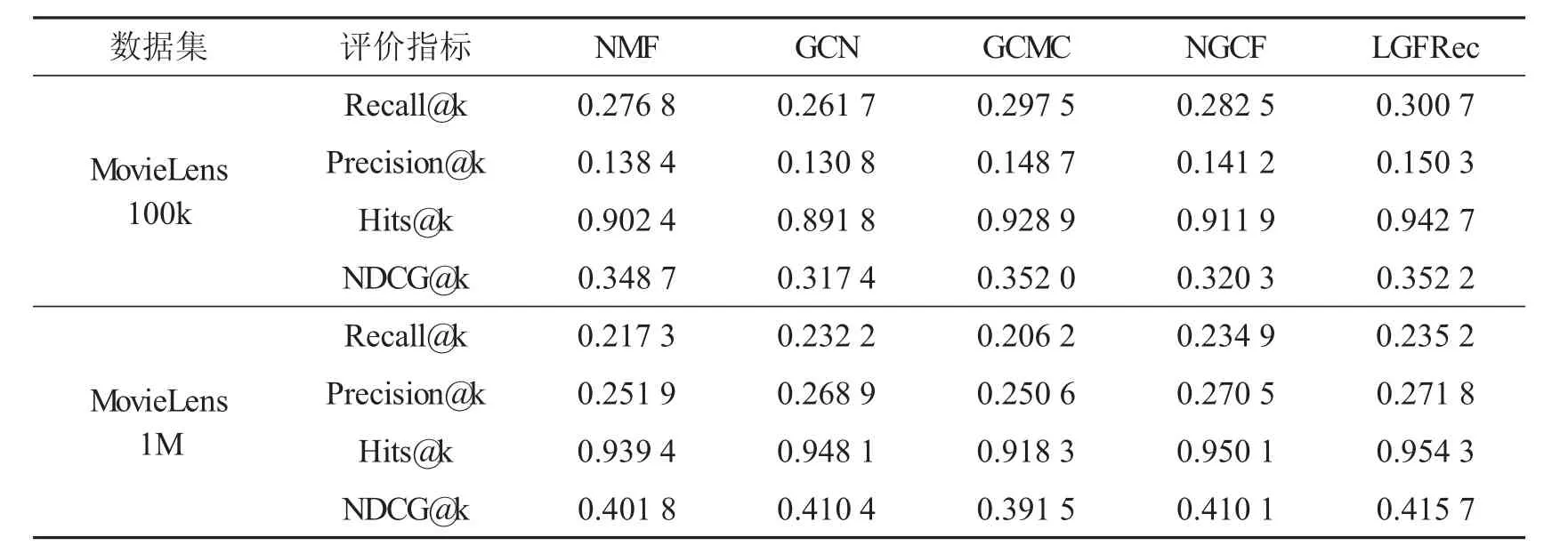
表3 有效性实验

基于表3的实验结果，我们有如下的实验分析和结论：

（1）图神经网络推荐模型如GCMC和NGCF通常优于传统的NMF，这是由于GNN能够更好的处理用户-商品交互图上的高阶偏好，进而取得一定的提升.

（2）为了进一步验证LGFRec模型对高频噪音的过滤，即低通图滤波器的有效性，我们移除了LGFRec模型中的低通图滤波器，此时模型退化为GCN模型.可以看出，在2个数据集上LGFRec模型可以显著GCN模型，这是因为GCN模型无法有效过滤和处理噪音信息，这会导致用户-商品表示及下游推荐任务的次优表现.

（3）本文所设计的LGFRec模型在MovieLens 100k的数据集上的4个指标均显著超过了其他4种模型.这有力证明了LGFRec能够有效过滤高频噪音并学习更加准确的用户-商品表示，进而提升了后续推荐任务的效果.

2.6 推荐列表长度

此外，取不同的推荐列表长度，即不同的K值，评估分数也会不同.对于本文的LGFRec模型，这里我们采集了当K从20变化至100时模型在MovieLens 100k与MovieLens 1M上各项指标的变化情况.

由图4和图5的实验结果来看，我们可以发现：当列表长度增加时精准度会下降，而其他指标均会上升.这说明当列表长度增加时虽然能尽可能预测所有用户感兴趣的商品，但更多地会增加用户不感兴趣的商品.这表示LGFRec模型有一定稳定性，在有噪音情况下仍然尽可能优先满足用户感兴趣的商品.

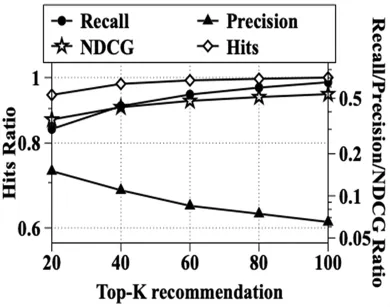
图4 MovieLen 100k上不同推荐列表长度的变化

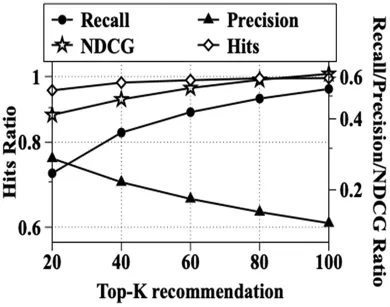
图5 MovieLen 1M上不同推荐列表长度的变化

2.7 稀疏度变化

同时，我们研究了我们的模型在不同用户-商品关系稀疏度下的变化.我们限制了MovieLens 100k训练集中用户-商品的交互数目，分别计算每个用户最多30，60，90和全部交互的情况下的表现，相应的稀疏度分别为0.021 98，0.031 92，0.041 92，0.062 9.

此时，在不同稀疏度下模型指标的变化如图6所示.从图中可以发现各项指标会随着数据量增加而升高，在稀疏度为0.031 92的情况下4个指标均大幅提高，之后分数趋于稳定.说明LGFRec模型能够利用较少数据达到较高预测精度，有较强的泛化能力，当用户不活跃时，模型仍旧能进行较精准的推荐.

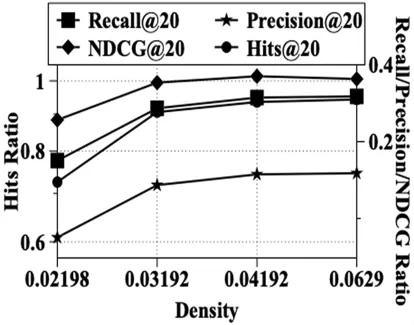
图6 MovieLens 100k上不同稀疏度的推荐效果

2.8 参数敏感程度实验

进一步地，我们进行了参数实验来研究LGFRec模型对于不同参数的敏感程度.

2.8.1 Dropout

为了探究对于交互信息的直接减少（message dropout）与节点信息的减少（node dropout）的区别，我们实验了在不同dropout下不同指标的性能变化，当测定其中一个dropout的影响时，另一种dropout值保持0.

从图7中可以发现以下3点：

（1）节点信息的减少对不同指标的影响是不同的.如当节点信息减少时，命中率先增大，再减小，而其他3种指标均为先增大，再减小，最后还会有所提高.这说节点信息减少时，模型更依靠交互信息对用户-商品交互的关系进行预测，直接导致部分商品未被列入推荐列表，命中率减少.

（2）交互信息的减少对模型影响总体而言是先增大后减小.同时观测到在交互信息dropout为0.2至0.4之间时四种指标都变化较少.说明数据交互信息本身存在一定噪音，LGFRec模型能将这些信息滤除，因此在这个区间内变化较少.

（3）两种dropout变化趋势完全不同，说明交互信息与节点信息为两种可以在不同层面影响模型预测效率的参数，因此在参数设置时需要分开考虑.

2.8.2 节点特征维度

为了发掘特征维度对模型的影响，我们设置了3种特征维度并观测其对于模型效果的影响，如图8所示.

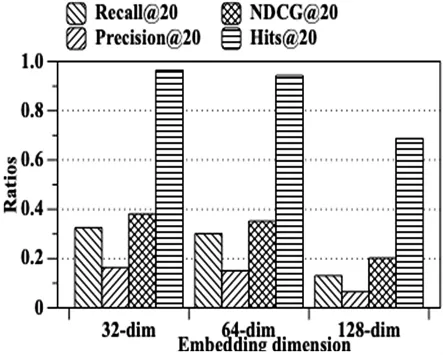
图8 LGFRec对于节点表示维度的敏感程度

基于图8的实验结果，我们发现：模型在特征维度为32和64时相差不大，但在128时会显著下降.这表明模型需要一定容量来保证效果，如选用32或64的维度.如果容量过大，维度大于64，会使得模型过拟合，造成准确率下降.

2.8.3 正则化系数

为了探究正则化参数对模型性能的影响，我们设置了{10－4，10－5，10－6}三组正则化参数并测试在该参数下LGFRec模型的效果，如图9所示.

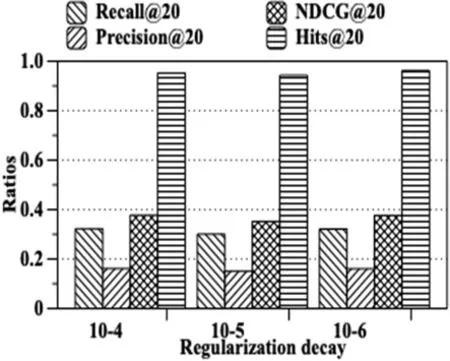
图9 LGFRec对于正则化系数的敏感程度

实验发现3种参数无明显区别，表明我们LGFRec模型已经有较强鲁棒性，对正则化参数不敏感，能够去除噪音，从而防止过拟合的情况发生.

2.8.4 滤波器层数

为了探究我们的LGFRec模型能否从多层低通图滤波中获益，这里改变了模型滤波的阶数K，并在图10中展示了滤波阶数为{1，2，3}时LGFRec模型的效果.

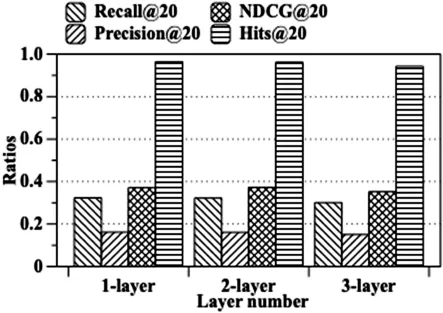
图10 LGFRec对于层数K的敏感程度

实验发现当层数增加时模型表现情况会逐渐降低，说明在MovieLens的推荐中用户和商品的信号逐渐复杂时，使用过深的体系结构可能会带来额外的噪声，使得模型过拟合.因此，用户-商品的协同信号仅需要考虑邻近的用户与商品即可.

3 结论

在推荐系统中，用户与商品的交互往往包含一些噪音连接（如误点击），进而降低了用户偏好建模的准确度.本文将用户和商品的交互建模为二部图，并从图信号处理的角度对其进行了降噪处理，进而有效提升商品推荐的准确度.具体地，本文设计了一种基于低通图滤波器的推荐模型LGFRec，其能够有效滤除高频的噪音交互，并有效保留用户的真实偏好交互.通过在两个数据集上与当前算法进行比较，本文在大量的实验结果上验证了所设计算法的有效性.