两类图的邻点可区别全染色

曹 蓉，林育青，童细心

（1.广东汕头幼儿师范高等教育专科学校，广东 汕头 515041；2.汕头职业技术学院自然科学系，广东 汕头 515041）

0 引言及概念

图的染色问题作为图论的一个重要内容，由于它重要的理论意义和实际意义，一直是人们研究的热点.2004年，Zhang等[1]首先提出了邻点可区别全染色的定义，并确定了圈、完全图、扇、轮、完全二部图、路、树的邻点可区别全色数.从此邻点可区别全染色得到了很多人的重视，但由于缺乏一个系统而有效的研究方法，至今大部分的成果都是针对一些特殊图去探索其邻点可区别全染色，也取得了一些研究成果[1-21].本文主要研究了轮环图kCn和图k×Cn的邻点可区别全染色，得到了它们的邻点可区别全色数.

定义1：[1]设图G是阶至少为2的连通图，k是正整数，f是 V（G）∪E（G）到{1，2，3，…，k}的映射，对任意v∈V（G），记.如果：

（ⅰ）对任意uv，vw∈E（G），u≠w，有f（uv）≠f（vw）；

（ⅱ）对任意uv∈E（G），有f（u）≠f（v），f（u）≠f（uv），f（v）≠f（uv），则f称为G的k－正常全染色.进一步，如果f还满足：

（ⅲ）对任意 uv∈E（G），有 C（u）≠C（v），

则f称为G的k－邻点可区别全染色（简记为k－AVDTC）.称

为G的邻点可区别全色数，记作χat（G）.

定义 2：[15]设 k1，k2，…，kn是非负整数，Cn＝v1v2…vnv1是有 n（n≥3，下同）个顶点 n 条边的圈，则称图 Cn＋{v1v11，v1v12，…，v1v1k1，v2v21，…，v2v2k2，…，vnvn1，…，vnvnkn}为（k1，k2，…，kn）轮环图，简记为 C(k1，k2，…，kn).ki均为零时，该图为圈 Cn；若 ki＝1，i＝1，2，…，n 时，该图为太阳图[16]，记为1Cn；当k1＝k2＝…＝kn＝k时，记为kCn（见图1）.

图1 轮环图kCn

本文所讨论的图都是阶不小于 2的无向简单连通图，V（G），E（G），Δ（G）和 d（v）分别表示图G的点集合、边集合、最大度和点v的度数，其它未加说明的定义和符号均来自文献[22].

1 结果及证明

综上可知，χat（kCn）＝k＋4，定理2得证.

推论1在图kCn中，把圈Cn上每个顶点的每一条悬挂延长为长度不小于2的路Pi，j所得到的图G，其邻点可区别全色数仍为χat（G）＝k＋4.

证明：结合引理2和定理2，结论显然成立.

推论2 在轮环图C(k1，k1，…，kn)中，若圈Cn上存在相邻的两个顶点有相等且最大数量的悬挂，即存在k＝kj＝kj＋1＝max{k1，k2，…，kn}，则其邻点可区别全色数仍为χat（C(k1，k1，…，kn)）＝k＋4.

证明：结合引理1和定理2，结论显然成立.

定理3柱图2×Cn的邻点可区别全色数χat（2×Cn）＝5.

图2 柱图k×Cn

综合情况1至情况5，当k≥3时，χat（k×Cn）＝6，从而定理4得证.

2 图例

根据定理1给出太阳图1C9和1C8的5－AVDTC如图3、图4.根据定理2，给出轮环图3C9和4C8的（k＋4）－AVDTC如图5、图6.根据定理3，给出柱图2×Cn的5－AVDTC如图7、图8.根据定理4，给出柱图k×Cn的6－AVDTC如图9、图10、图11、图12和图13.

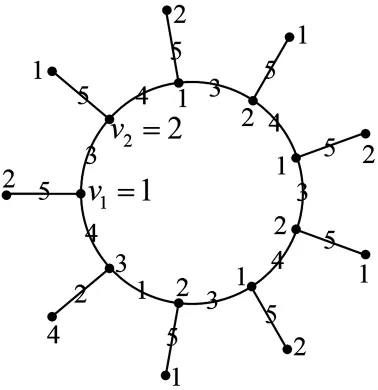
图3 C9的 5－AVDTC

图4 1C8的 5－AVDTC

图5 3C9的7－AVDTC

图6 4C8的 8－AVDTC

图7 2×C9的 5－AVDTC

图8 2×C8的 5－AVDTC

图9 5×C9的 6－AVDTC

图10 4×C9的 6－AVDTC

图11 5×C8的 6－AVDTC

图12 4×C8的6－AVDTC

图13 7×C3的6－AVDTC