基于偏好型支持向量机的遥感图像云检测技术
杜家昊,周 晴,赵文杰
(1.中国科学院国家空间科学中心 复杂航天系统电子信息技术重点实验室,北京 101499; 2.中国科学院大学,北京 101408)
0 引 言
根据国际卫星云气候计划观测数据,全球67%以上区域时常被云层覆盖[1]。云的覆盖会导致遥感图像信息缺失,甚至无法使用,浪费了卫星宝贵的存储空间[2]。因此高效、准确的云检测算法对遥感卫星在轨应用具有重要意义。
目前的云检测方法,大致可分为3类:基于阈值的方法、基于传统机器学习的方法和基于深度学习的方法。基于阈值的方法是利用云和其它地物在不同光谱范围内的反射率差,人工设置阈值和特征提取规则来识别云和下垫面[3]。此外,许多算法结合了多时间信息[4]、空间信息[5]和动态阈值[6]。随着机器学习技术的兴起,传统的机器学习算法如人工神经网络[7]、支持向量机[8]和随机森林[9]已经被用于云分类问题。与基于阈值的方法相比,它们消除了阈值设置的问题,并且特征选择更加灵活[10]。最近,基于深度学习的云检测方法诸如卷积神经网络[11]、SegNet网络[12]、注意力机制[13]等,在遥感应用领域取得了显著突破。基于深度学习的方法可以自动提取重要特征[14],在训练样本充足的情况下,该方法往往具有较高的精度和较强的泛化能力,但实现复杂。
然而,目前的大多数云检测方法对于与云特征相似的下垫面如雪地、沙漠、冰原等高亮地物往往无能为力[15]。为此,本文提出了一种基于PSVM的遥感图像云检测技术,既能准确区分云和一般地貌,同时对于许多难以区分的特殊下垫面也能准确识别。
1 图像纹理特征提取
在遥感图像云检测中,图像的灰度分布是影响图像特征的重要因素[16],而纹理特征是当图像灰度按照一定规律变化时,整体会呈现出的一种周期性的视觉现象。本文提取图像的纹理特征主要分为3个步骤,即图像灰度共生矩阵的提取、灰度共生矩阵的归一化处理和图像纹理特征值的计算。
灰度共生矩阵通过图像的空间相关性来描述图像的纹理特征。在提取灰度共生矩阵前,首先要将图像转化为灰度图,之后使用式(1)对图像进行压缩,以提高算法的运算速度。其中图像压缩后的灰度等级为k,通过实验,本文选取k=16
Ave=INT[Ave/(256/k)]
(1)
我们将压缩好的图像分成N×N的子块,假设图像子块中任意一点 (x,y) 处的灰度值为g1,它附近的另一点 (x+i,y+j) 处的灰度值为g2,这两点的灰度值构成一个灰度点对 (g1,g2)。 构建一个k×k的方阵,将每个灰度点对的所有出现次数写入灰度点对对应的行和列,即可得到灰度共生矩阵,如图1所示。其中i和j的大小决定了提取的是粗纹理还是细纹理,i和j的正负反映了图像所提取的纹理方向θ,有0°、45°、90°和135°这4种情况,一般选取θ=0°。
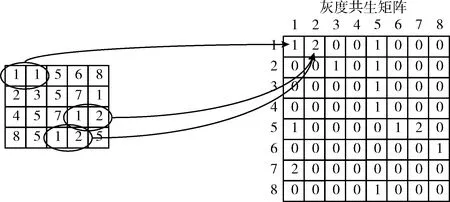
图1 灰度共生矩阵的计算方法
在得到图像的灰度共生矩阵后,可以发现,不同尺寸的图像所包含的像素点个数是不相同的,图像越大,其灰度共生矩阵中元素的取值也就越大,因此需要对灰度共生矩阵进行归一化,使其适应不同大小的图像。假设图像的大小为N×N,灰度共生矩阵应按照式(2)进行归一化,归一化后的灰度共生矩阵也被称为联合概率矩阵
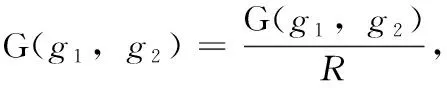
(2)
根据联合概率矩阵,分别计算出图像的能量、对比度、逆差矩、熵、自相关性等图像的纹理特征指标
(3)
式(3)为图像能量的计算公式,其中k为图像的灰度级数,它是将联合概率矩阵中的所有元素取平方之后相加得到。如果图像的纹理均匀、单一,则能量会有较大值,它反映了图像纹理的粗细度和分布的均匀程度
(4)
式(4)为图像对比度的计算公式,如果联合概率矩阵中偏离对角线的元素有较大的值,则对比度较大。因为偏离对角线的元素是图像中灰度值跳变较大的点对,所以对比度反映了整个图像像素值的亮度变化快慢情况
(5)
式(5)为图像逆差矩的计算公式,即如果联合概率矩阵对角线元素有较大的值,则逆差矩值较大,它反映了图像局部纹理的同质性,图像内部纹理越均匀,逆差矩越大
(6)
式(6)为图像熵的计算公式,当联合概率矩阵值分布不集中时,熵具有较大的值,反之,熵具有较小的值。熵是对图片随机性和信息量的度量,当图片中的噪声很大或者图片纹理特征随机性较强时,熵具有较大的值,反之,熵具有较小的值
(7)
(8)
式(7)和式(8)为图像的自相关性计算公式。当图像的联合概率矩阵中各元素值均匀且相等时,即图像的纹理较为均匀时,图像的自相关性较大,反之,自相关性较小。自相关性总体来说反映了图像在某个方向上的纹理一致性。
2 基于PSVM的遥感图像云检测技术
2.1 数据预处理
作为最成功的地球观测计划之一,Landsat计划为卫星遥感的科学和应用做出了巨大贡献,其开放和免费的数据政策使得全球受益。本文所用到的遥感图像数据均来自地理空间数据云网站(http://www.gscloud.cn/)的Landsat系列卫星。本文首先选取了多个具有典型特征的云和下垫面图片600张,将其中的500张图片作为训练集,50张作为验证集,余下的50张图片作为测试集。
对选取的600张图片的云区和下垫面区域进行人工标识,之后程序自动对图片进行分块处理,子块大小为N×N。算法自动统计每一个子块中的云量,将云量超过60%的子块自动分类为云子块,将云量低于20%的子块分类为下垫面子块,其余子块自动剔除。
使用式(1)至式(8),提取所有云和下垫面子块的能量、对比度、熵、逆差矩、自相关性和平均灰度值6个特征,以N=60为例,提取到的特征值见表1。由于不同的特征值取值范围不同,因此需要对特征值进行归一化处理,将所有特征值映射到区间[0,1]。
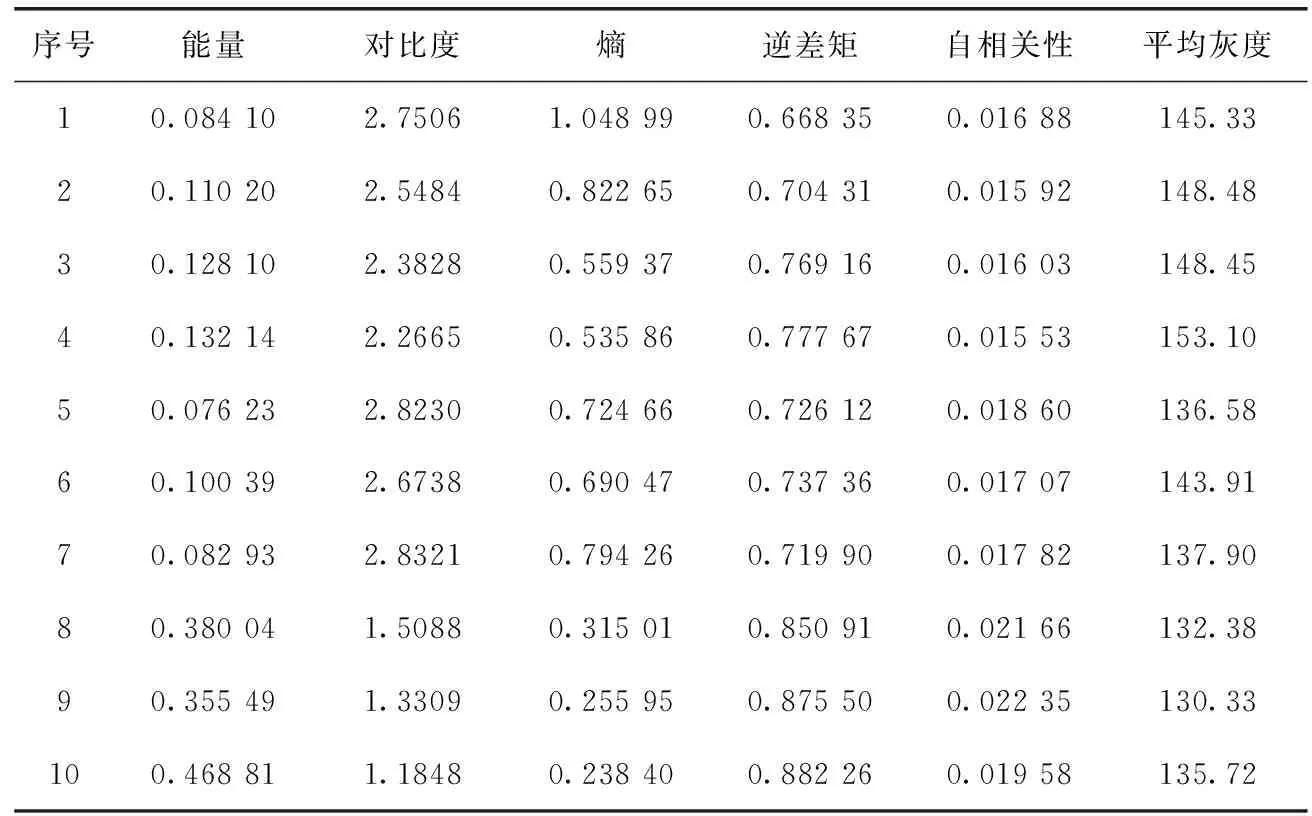
表1 图像特征值(节选)
2.2 遥感图像云检测方案设计
SVM是一种针对分类和回归问题的统计学习理论[17]。如图2所示,SVM的主要目的是寻找一个最优的二分类超平面使两类样本间的分类间隔最大[18]。其中ω和b分别为超平面的法向量和截距,Margin为样本间的分类间隔。
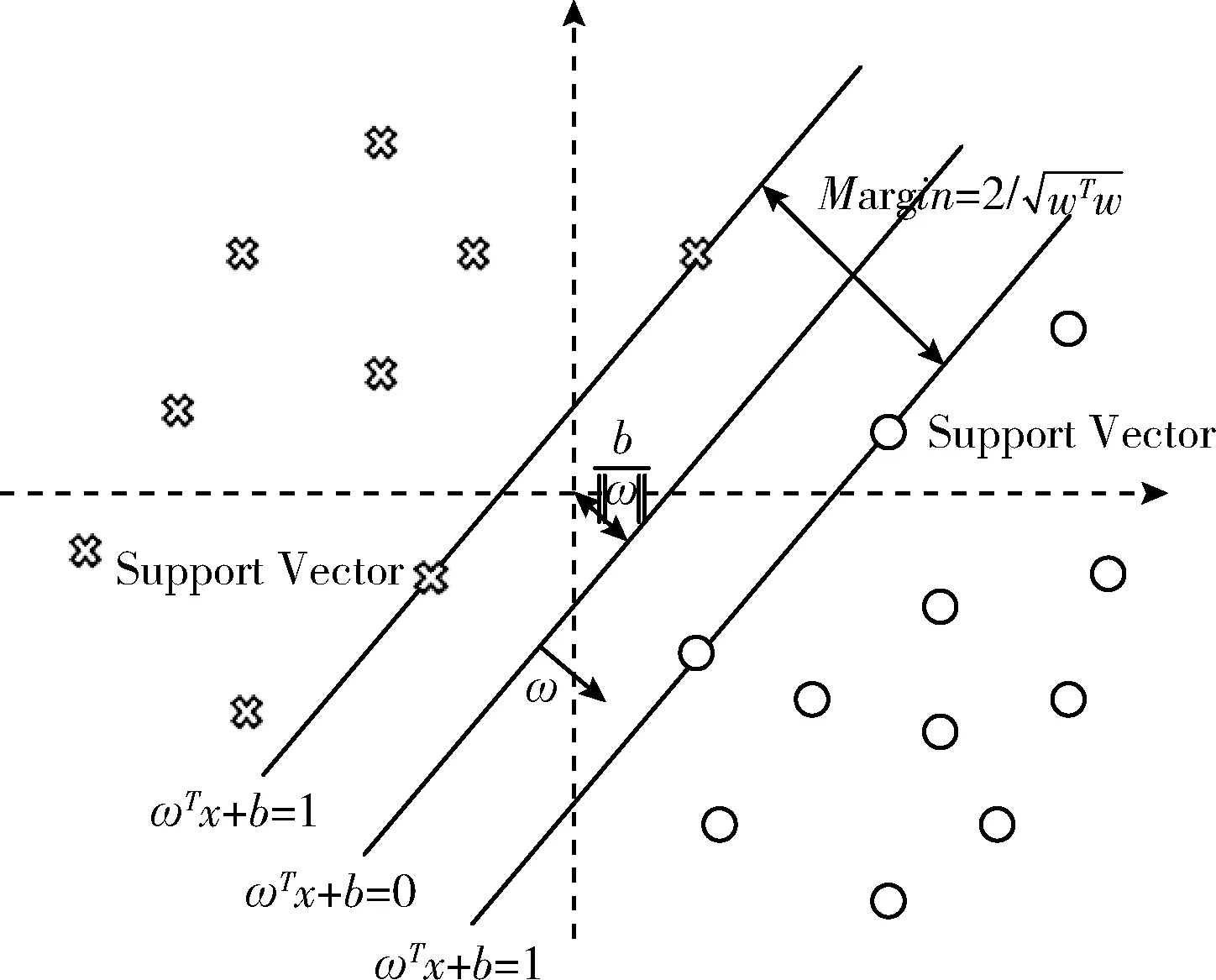
图2 SVM分类原理
根据2.1节得到的训练样本数据,建立SVM分类器,利用训练样本 (xi,yi) 求解如下的二次优化问题
(9)
(10)
式中:αi和αj为拉格朗日乘子,C为惩罚因子, K(x,xi) 为核函数。核函数将高维特征空间的非线性运算转换为原输入空间的核函数计算[19],避免了“维数灾难”。目前常用的核函数有4种,分别是线性核(LINEAR)、多项式核(POLY)、径向核(RBF)和Sigmoid核
K(x,xi)=exp(-γ|x-xi|2)γ>0
(11)
本文选取径向核函数,它可以将样本映射到无限维的空间中,是应用最广的核函数。同时核函数中只有一个参数,计算量少,便于调参[20]。式(11)为径向核的计算公式,γ为核函数的一个待调整参数。选取合适的C和γ值,使用OpenCv库提供的SVM分类器,输入训练样本,开始训练。之后读取验证集中的样本和标签,使用训练产生的svm.xml模型文件对这些数据进行验证,以检验训练模型的准确度,若模型在验证集中准确率较低,则调整参数C和γ,重复上述训练和验证过程,直至得到满意的结果。本文最终选取C=10,γ=0.01。使用训练产生的svm.xml文件对测试集图像子块数据进行测试,将测试得到的结果和测试集标签进行比对,以测试训练得到的模型的准确度。
在对遥感图像进行云检测时,先将待检测图像划分成若干个子块,再使用分类器逐一进行判断,将云子块涂成白色,将下垫面子块涂成黑色,得到的新图像即为云检测结果。遥感图像云检测流程如图3所示。
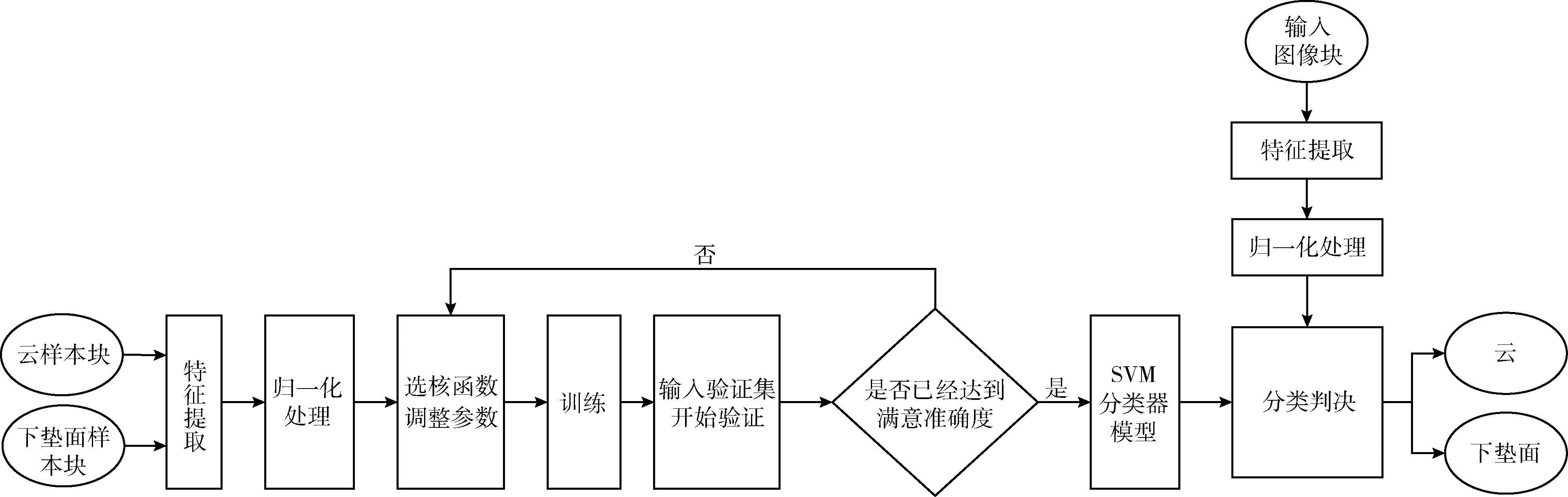
图3 云检测算法方案设计流程
2.3 基于PSVM的改进方案设计
尽管使用2.2节的方案进行Landsat卫星图像云检测已经达到了一个不错的效果,例如,当N=60时,分类器对于绝大多数的云和下垫面分类准确率为97.46%,第3章中将给出更为详细的数据。但是,针对某些特殊的下垫面,例如雪地、高亮的山脉或地表等和云相似的地物时,分类器常常把它们错分类成云。
在实验初期,我们尝试将雪地等特殊下垫面加入到下垫面子块的训练集中,尽管这样做保证了训练集的完整性,但是分类器常常表现出糟糕的判别结果,不但不能准确地识别特殊下垫面,甚至对于许多云和一般下垫面也常常分类错误,分类准确率大大降低。为了让分类器能够准确地区分绝大多数的云和下垫面,我们先将包含特殊下垫面的卫星遥感图像从训练集中剔除,再进行训练。
虽然雪地等特殊下垫面与云的灰度值及纹理特征较为接近,但是分类器真的就无法将二者区分吗?通过将云、特殊下垫面和一般下垫面的能量、对比度、逆差矩、熵、自相关性进行分析比较,我们发现,相比于一般的下垫面,云和特殊下垫面的特征值较为接近。但是单独对比云和特殊下垫面的特征值,它们之间依然有一定的差别,只是这一差别相比于云和一般下垫面表现得微乎其微,因此分类器难以将云和所有类型的下垫面准确区分,但是却可以准确地将云和特殊下垫面区分开。
针对这一发现,本文提出了一种PSVM算法,将下垫面样本块中的所有非特殊下垫面去除,仅保留特殊下垫面和云作为训练集,进行训练,得到一个SVM模型,记作SVM_S。由于训练集包含了完备的云样本集和不完备的下垫面样本集,因此训练得到的SVM模型对云样本有较高的判别准确度,且能较好地区分云样本和特殊下垫面样本,但容易将其它下垫面样本误判为云。为此,我们再将下垫面样本中所有特殊下垫面去除,只保留一般下垫面和云作为训练集,进行训练,得到另一个SVM模型,记作SVM_G,与上一步得到的模型共同实现云判别。
在对遥感图像进行云检测时,本文同样采用分块判断的方式实现。为了减小云检测过程中算法的误判对整体效果的影响,本文对分块过程进行了改进,采用重叠分块的方法,以提高检测效果。步长为S,分块大小为N,从左至右,从上至下,逐块对图片进行云检测。改进的图片检索流程如图4所示。

图4 改进的图片检索流程
对于任意一个测试样本图片,首先将图片重叠划分成N×N的子块,步长选取12。之后采用SVM_S对各个子块进行判别,若判别为云,则采用SVM_G对该子块进行二次判断,并取SVM_G的判别结果为最终结果,若判别为下垫面,则直接将SVM_S的判别结果作为最终结果。算法流程如图5所示。
3 实验结果
本文首先验证了不同N值对识别效果的影响,不同实验分组所选取的训练集样本和测试集样本均是由前文所述的600张Landsat卫星遥感图像采用相同的步长使用重叠切片的算法划分得到,数量基本相同。不同N值对算法识别效果的影响见表2,在这里训练集和测试集中不包含特殊下垫面样本。其中,SVM_GU表示SVM_G对一般下垫面的识别准确率,SVM_GC表示SVM_G对云的识别准确率,SVM_GA表示SVM_G的平均识别准确率。
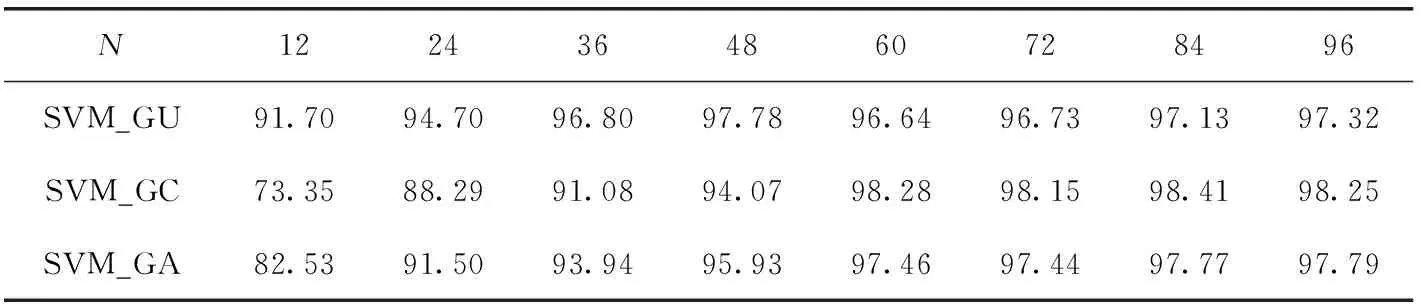
表2 传统SVM不同切片大小识别准确率对比/%
接下来,本文对提出的PSVM方法的识别准确率进行了测试,见表3。其中,SVM_PU表示本文提出的方法对一般下垫面的识别准确率,SVM_PC表示本文方法对云的识别准确率,SVM_PA表示本文方法对云和一般下垫面的平均识别准确率,SVM_PS表示本文方法对特殊下垫面的识别准确率。
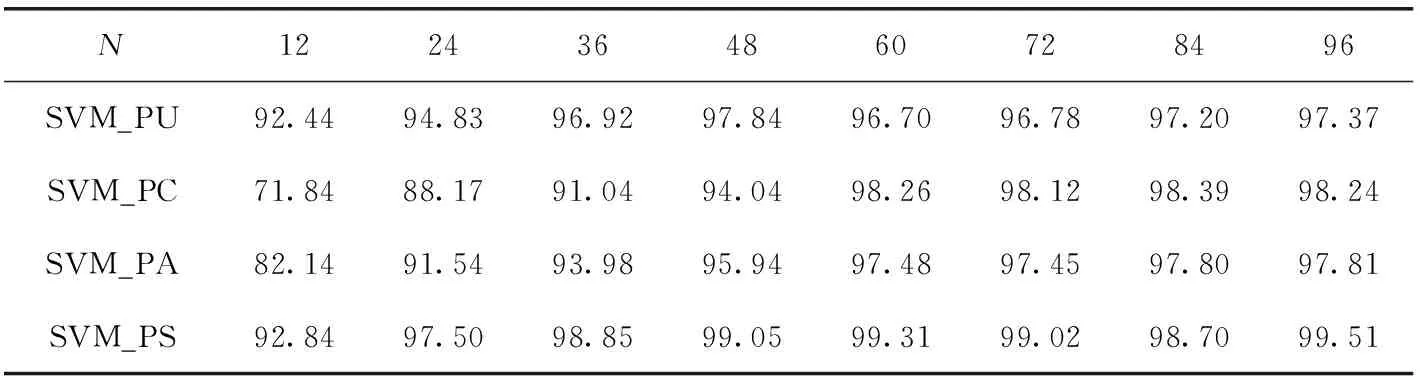
表3 PSVM方法不同切片大小识别准确率对比/%
最后,本文使用包含特殊下垫面在内的完备训练集进行训练,得到的训练模型记作SVM_G2,再在各个测试集上测试,见表4。其中,SVM_G2U表示SVM_G2对一般下垫面的识别准确率,SVM_G2C表示SVM_G2对云的识别准确率,SVM_G2A表示SVM_G2对云和一般下垫面的平均识别准确率,SVM_G2S表示SVM_G2对特殊下垫面的识别准确率。
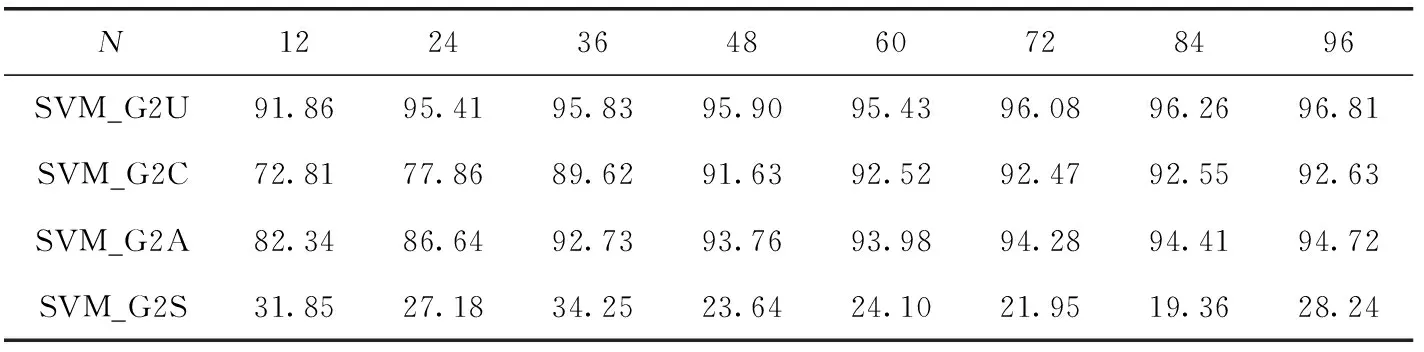
表4 加入特殊下垫面对SVM识别准确率的影响/%
接下来,本文对比了传统支持向量机(SVM_G)、加入特殊下垫面训练的传统支持向量机(SVM_G2)与本文提出方法(SVM_P)的平均识别准确率,如图6所示。实验结果表明随着N值的增加,算法识别准确率逐渐增加。当切片大小增加到60时,识别准确率已经达到一个较高的值,尽管继续增大切片大小识别准确率依然呈上升趋势,但增加有限,同时较大的切片大小不利于对图像云区域的精确识别,因此本文选取切片大小为60。之后,对比SVM_G2A与SVM_GA可以看出,将特殊下垫面加入到训练集中不但不能帮助我们准确区分云和特殊下垫面,还会降低训练模型识别一般下垫面和云的准确率。以N=60为例,与SVM_G中的数据相比,SVM_G2下垫面样本的识别准确率降低了1.21%,云样本的识别准确率降低了5.76%,综合识别准确率降低了3.48%。最后,综合对比3个方法的识别准确率,可以得出,当N大于等于24时,本文提出的算法对云和一般下垫面的识别准确率最高。以N=60为例,本文算法综合识别准确率为97.48%。与传统的支持向量机97.46%的准确率相比,提高了0.02%。这是由于在一般下垫面的遥感图像中,时常也会存在少量与云特征相似的特殊下垫面,而本文的算法能够将这些下垫面较为准确地识别出来,尽管对于云的识别准确率略有降低,但综合准确率有所提高。
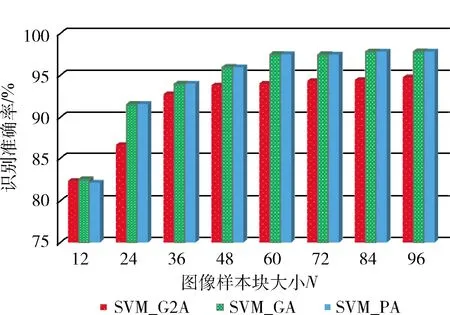
图6 平均识别准确率对比
本文还对比了加入特殊下垫面训练的支持向量机(SVM_G2)和本文提出的方法(SVM_P)对特殊下垫面的识别准确率,如图7所示。可以看出,本文提出算法对特殊下垫面的识别准确率远高于传统的支持向量机算法,以N=60为例,本文提出的算法对特殊下垫面的识别准确率为99.31%,而传统的支持向量机算法识别准确率仅为24.1%,准确率提升了75.21%。
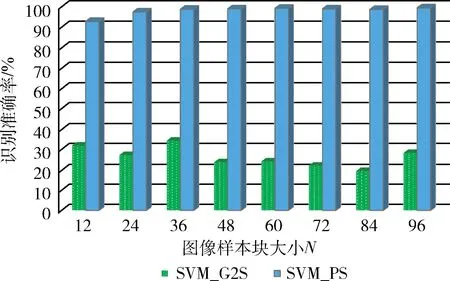
图7 特殊下垫面识别准确率对比
使用PSVM算法选取N=60对包含特殊下垫面在内的完整测试集进行测试,得出本文算法的综合识别准确率为97.66%。本文算法对遥感图像的识别效果如图8所示。

图8 本文算法识别效果
从图8中可以看出,算法对于绝大多数的下垫面都能准确识别。上述图片使用传统的支持向量机也能够准确识别,然而,对于雪地等特殊的下垫面,一般方法往往会出现大量的误判,而本文提出的PSVM算法在兼顾一般遥感图像识别效果的同时,对于包含特殊下垫面的图像也有不错的识别效果。传统的支持向量机与本文算法对特殊下垫面的识别结果对比如图9和图10所示。

图9 传统支持向量机对特殊下垫面识别效果

图10 本文算法对特殊下垫面识别效果
4 结束语
本文提出了一种基于PSVM的遥感图像云检测算法,通过使用提取到的云和下垫面的纹理特征,训练产生支持向量机模型,对Landsat系列卫星遥感图像进行云检测。针对雪地等特殊下垫面难以区分的问题,本文将云和特殊下垫面的纹理特征单独提取出来,进行偏好训练,产生只对特殊下垫面敏感的SVM模型,并与前面训练所得到的模型进行联合判断。通过这种方式,分类器能够准确区分云和各类下垫面,极大地提高了分类广度和识别准确率,为后续遥感图像云检测提供了又一个创造性思路。
实验结果表明,与传统的SVM算法相比,本文算法对云和一般下垫面识别准确率提高了0.02%,对特殊下垫面识别准确率提高了75.21%,性能提升显著。后续我们将收集更多卫星的遥感图像进行训练并优化算法,以提高模型的泛化能力和算法的运算速度。

