设计任务型预学作业提高学生数学学习效能

2022-05-21 06:01顾利国严育洪

辽宁教育 2022年7期

顾利国，严育洪

（江苏省无锡市后宅中心小学，江苏省无锡市锡山区教师发展中心）

在《辞海》中，“作业”解释为“为完成学习方面的既定任务而进行的活动”，而“既定任务”很多时候可以定在学习之前，此时的作业就不再单纯是课后巩固性作业，也可以是课前准备性作业。这样，作业的功能可以得到极大的扩展。这种“为完成学习之前的既定任务而进行的活动”的准备性作业，让我们对由此设计的预学活动有了新的理解，它不应该只是“知识的预习活动”，还应该是“学习的预热活动”。

美国学者安德生在《提高教师教学效能》一书中对“作业”的描述为：“学习任务大部分是由教师分配的，所以每项任务通常被称为‘作业’（assignment）。我们更喜欢‘任务’（task）这个术语，因为任务的概念赋予了指定活动的目的。”把传统作业设计成“赋予了指定活动的目的”任务型预学作业，并用至课前预学环节，替代预习提纲这样的传统预习形式，可提高预学活动的效能，使作业不再独立于学习之外，而成为学习的一部分贯穿始终。任务型预学作业既是学习成效的检测工具，也是学习行为的启动“钥匙”。

传统的预习提纲，很多时候都是设计成一些问答题的形式，学生题目做多了，做久了，会觉得枯燥乏味。而任务型预学作业指的是一种表现性活动，契合学生喜欢表现的年龄特点。同时，任务型预学作业因为具有综合性特点，所以常常具有挑战性，也激发了学生的好胜之心。用任务型预学作业替代传统预习提纲，能够使学生产生更强的学习动力。经实践研究我们发现，任务型预学作业有以下五种提高学习效能的驱动类型。

一、尝试性任务预学作业

在教学与计算相关内容时的练习阶段，传统的预习方式经常采用让学生“看题（例题）、答题（问题）”的单一形式，过细的问答使预学缺乏挑战，学生缺乏学习的热情。设计尝试性任务预学作业，就是变“看题”的预习提纲为“做题”的预学作业，可以在后设的“固学”环节中选择一道与例题同质异形的计算题（往往是教材中的巩固习题），前置设计成尝试性任务让学生解答（如图1）。学生如果不会，就会主动去预学例题中的算法与算理；学生如果会，也会主动去预学例题以检查自己的解答是否正确。课上，教师可以组织预学的展示活动，让做错的学生说做法，做对的学生做“小老师”进行讲解，教师只需在问题或知识的关键处进行点拨引导即可。

图1 尝试性任务预学作业流程

除了把“看题”的简单问答变成“做题”的努力尝试之外，教师还可以设计“编题”的预学作业，设计让学生根据例题自行编题的表现性任务。学生在编题时需要主动去看例题，除了研究例题的算法与算理，还需要研究例题的类型与特征，这样的“研学”过程，也就达到了“预学”的目的。由此可见，与“做题”任务相比，这样的“编题”任务更加高效，学生的热情更高，学生编的题目还可以让同学去做，这样可以做“小老师”，充分表现出自己的智慧。

预学教材时，我们让学生养成有困难可以寻求“外援”的习惯。学生可以先向教师申请预习提纲，根据提示和帮助来自学教材。与传统做法不同的是，对学生的“预学”，我们强调“独学”，鼓励学生自学，在学生遇到困难时再借助预习提纲帮助自学。因为学生需要，所以此时预习提纲就能起到“雪中送炭”的作用，受到学生欢迎；如果学生的自学还是有困难，那么除了借助“物（预习提纲）”，还可以借助“人”的力量，先向所在小组同学请教，进入“组学”环节；如果学生还是有困难，就可以进入全体学生甚至教师参与的“共学”环节。

二、操作性任务预学作业

与“写”作业相比，学生更喜欢“做”作业，这也是传统预习提纲难以被学生喜欢的一个原因。我们可以把一些能动手操作特别能制作作品（产品）的作业设计成“做”的任务，不管学生会不会做，他们都会主动预学“做”作业所需的知识技能，并用这些知识技能指导或检查自己做得是否正确。

例如，教学“认识线段”之前，我们让学生完成“画一条线段”的操作任务。有些学生具备相关的生活经验，会画线段，但要确认画得是否准确，也需主动开展自学教材或与同学交流等预学活动；有些学生没有相关生活经验，不会画线段，更需主动进行预学活动。课上，我们使用学生的作品作为教学素材，在学生的评说中适时评讲。“共学”之后，可让学生画完原来没画完的作品或画好原来没画好的作品，也可重新再画一条线段（“固学”）。

如果任务改成“画一条6 厘米长的线段”，学生必须弄明白两个新概念“线段”和“厘米”，这样能达成“延学”（如图2），连续帮助学生预学“认识线段”和“认识厘米”两课内容。由此可见，与“画一条线段”相比，“画一条6 厘米长的线段”的任务关联范围更大，对学生的挑战也更大。

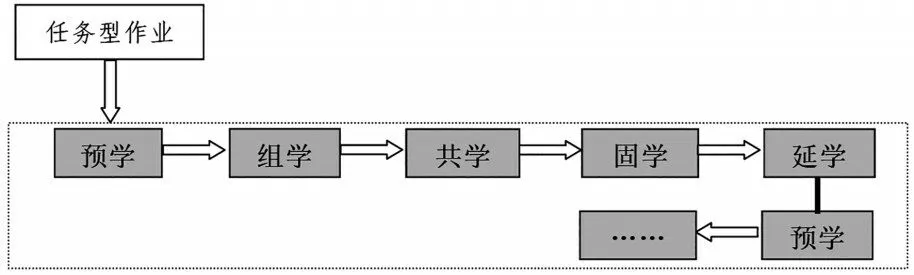
图2 操作性任务预学作业流程

若学生制作的作品不仅看得见、摸得着，还能用得上，这样的任务就能激发学生“做”的兴趣。在教学“年月日”之前，我们让学生完成“做一张新年年历”的制作任务，学生预学时先要清楚“画几大格”，也就是“一年中有几个月”，然后要清楚“每大格画多少小格”，也就是“每个月有多少天”。这样制作完成的作品学生不仅可以自己用，还可以送给同学、朋友、父母、亲人或教师，这时作品就变成了礼物。我们还布置了“用硬纸板做一只圆柱形笔筒送给同学”的制作任务，学生主动预学“圆柱的认识”等知识。因为要送给同学，很多学生还会进行美化，画上一幅画，抄上一首诗，写上一句话。

若学生制作的作品不仅看得见、摸得着，还能吃得好，这样的任务学生就更有“做”的渴望。在学习“比和比例”单元之前，我们就布置了“跟我学做奶茶”“跟我学做酸梅汤”等制作任务，很好地调动起了学生的预学兴趣。

三、思辨性任务预学作业

在数学教学中，重难点知识大都需要学生去探究和思考。我们设计思辨任务，通过核心问题，引导学生开展预学活动。对重点知识的掌握、对难点问题的突破需要伸展到“共学”环节，设计思辨性任务预学作业，可把传统教学中学生在“共学”环节才产生的疑惑前置（如图3）。

图3 思辨性任务预学作业流程

其一，从一些知识的名称上，我们就可以找到让学生思辨的问题，如“小数是‘小’数吗”，为了弄清楚这样定义是否正确，学生就会主动预学“小数的认识”，之后经过“组学”“共学”最终形成共识：小数可以表示比1 小的数，但不一定是比1 小的数。再如，“倒数是怎样的‘倒’数”，这样的名称会驱动学生预学“倒数的认识”。课上，我们用此问题作为议题，组织学生展开讨论，检测预学成效，交流预学成果。学生对“1 的倒数是1”有争议，有的学生认为它没有“倒过来”，有的学生认为它是特殊情形，还有的学生认为“倒过来”只是倒数的形式，本质是“乘积是1 的两个数”。讨论到最后，有的学生质疑：“学了倒数有什么用？只是玩玩数字游戏么？”教师顺势就可让学生带着疑惑预学“分数除法”内容。

有一些数学知识的名称还会引起歧义，教师同样可以借题发挥，设计议题让学生思辨，开展预学活动。如“三角形的稳定性”，很多学生会把“稳定”理解成“稳固”，教师可以布置思辨任务，让学生展开预学。课上，学生各抒己见，教师指导学生明白知识的本质——“三角形的稳定性”其实说的是“三角形的确定性”。

其二，从一些知识的关系上，我们也可以找到让学生思辨的问题，如“百分数是分数吗”的思辨任务，就能帮助学生预学“百分数的认识”。在“组学”环节，有的学生认为“百分数是分母100 的分数”，对此有学生提出异议，认为“百分数是分母100 的分率”，还有的学生产生疑惑：“有了分数，为什么还要学习百分数？”这一思辩问题在学生的同感中又成了思辨任务，将课堂教学引入“共学”环节，引发全班大讨论。再如，我们提出的“‘平行’的反义词是‘垂直’吗？”的思辨任务，驱动学生预学“平行与垂直”这一单元。经过思辨，学生认识到“平行”的反义词是“相交”，“垂直”是“相交”的特殊情况，“平行”与“垂直”不是并列关系。此时，有学生认为课题“平行与垂直”中用“与”不太合适，容易让人误以为“平行”与“垂直”是并列关系。

其三，供学生思辨的问题需要在后续教学中才会显现，如教学“面积”知识时，可以与学过的“周长”知识进行思辨，从概念意义的比较到计算方法的比较，让学生在比较中学习，可以有效防止知识的混淆。

四、阅读性任务预学作业

我们认为，数学阅读不仅是对数学知识的阅读，也包括利用数学知识阅读。“用数学知识阅读”也可以成为学生预学的驱动力。它不仅需要学生的数学阅读能力，更需要学生具有数学解读能力，要用数学解读材料，先要学好数学。

在教学中，“用数学知识阅读”更多是对数学知识的运用或对数学知识的拓展，往往放在“延学”环节。对此，我们同样可以采用“以终为始”的策略将之前置，为“预学”服务（如图4）。

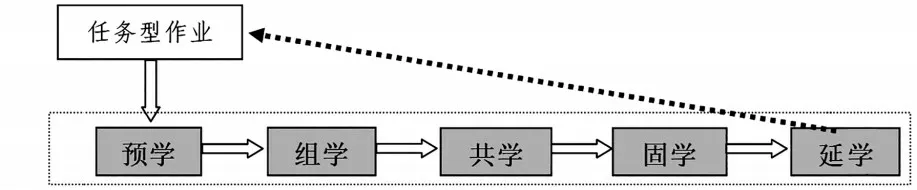
图4 阅读性任务预学作业流程图

例如，我们设计了让学生“用数学语言解读成语‘水涨船高’”的任务，带动学生主动预学“正比例的意义”。然后，换一个成语“立竿见影”，帮助学生主动预学“用正比例知识解决实际问题”。

除了解读一个词，我们还可以用解读一句话的方式来帮助学生预学数学知识。如古希腊数学家毕达哥拉斯曾说“一切平面图形中最美的是圆”，学生读了这句话，很想知道为什么，于是主动预学“圆的认识”，从中去寻找答案。

阅读一首诗也能带动学生预学数学知识，如阅读杜甫的《饮中八仙歌》：“李白斗酒诗百篇，长安市上酒家眠。天子呼来不上船，自称臣是酒中仙。”教师提出解读任务：“诗中提到了‘斗’，‘1斗’有多少？”学生查阅资料知道：“斗，十升也。”也就是要知道“1斗有多少”，先要知道“1升有多少”，由此带动学生预学“升和毫升”的数学知识。

阅读一本书也能带动学生预学数学知识，如当学生读到《红楼梦》第62 回中的一段话：“一年十二个月，月月有几个生日。人多了，就这样巧，有两个一日的，也有三个一日的”，我们配上“红楼梦中有名有姓的人物有732 人”的统计数据，引导学生预学“用假设策略解决问题”来完成解读任务。

五、猜想性任务预学作业

美国教育家杜威认为，生长就是通过行动不断地向前发展，“这个朝着后来结果的行动的累积运动，就是生长的涵义”。在数学教学中，知识也在朝着后来结果不断累积，我们可以把后续知识看成前有知识不断生长的结果。教师可以设计猜想性任务，让学生根据知识的“生长”过程、“运动”轨迹不断创造出知识。

在学习“2的乘法口诀”之后，学生就很容易猜想出接下来会学“3的乘法口诀”。学了“3的乘法口诀”之后，我们提高难度，要求学生不仅猜想接下来会学什么，而且创想“4 的乘法口诀”会有几句，学生观察“2 和3 的乘法口诀”，猜想“4 的乘法口诀”会有4 句，经过预学，学生发现猜想正确。等到学“5 的乘法口诀”，我们让学生完成“创编5的乘法口诀”的任务，再预学检查创编是否正确。之后教学“6～9 的乘法口诀”，我们使学生明确了作为“小老师”的任务目标。

对并列式知识，我们既可以设计“由始到终”的猜想任务，也可以设计“以终为始”的猜想任务（如图5），让学生围绕最终的任务要求从起点开始预学。

图5 猜想性任务预学作业流程

我们设计了“编写一个数的倍数特征的教材”任务，使学生主动预学“2 的倍数特征”教材，学生不仅要预学知识的探究方法，而且要预学教材的编写方法，然后以此为模板，完成其他数的倍数特征的教材编写任务。此中，“2的倍数特征”教材就成了完成任务的一份“说明书”，“2的倍数特征”的教学就成了完成任务的一节“种子课”。

对递进式知识，为了便于学生猜想，我们可以指导学生用框架图、知识树把知识的生长过程和运动轨迹画出来。如“倍数和因数”一课，我们设计平行任务，分别提出预学的不同要求。第一步，提出思辨任务：“这里的‘倍数’与之前学过的‘倍数’意义一样吗？”带动学生预学“倍数和因数”中关于“倍数”的内容；第二步，提出猜想任务：“你会根据倍数的意义，反向猜想因数的意义以及求一个数因数的方法吗？”带动学生预学“倍数和因数”中关于“因数”的内容。之后，有了这些“种子知识”，学生就可以继续描画知识的发展蓝图，由“一个数的倍数”衍生出“两个数的公倍数”，然后相应地猜想“一个数的因数”到“两个数的公因数”，最后“最小公倍数”与“最大公因数”等知识也就能水到渠成。