多式联运可靠性测度研究

伍景琼，张 旭，苏 娜，黄文骁

(1.昆明理工大学 交通工程学院，云南 昆明 650500； 2.成都工贸职业技术学院，四川 成都 610000)

0 引言

随着采购策略的转变，大多数工业企业为减少成本，在不断降低原材料的库存量加速库存周转的同时，要求提高原材料多式联运的可靠性来有效降低停产风险，达到即降低成本又保障生产的目的。

近年来，国内外学者越来越关注多式联运系统可靠性的研究，在多式联运可靠性测度方面，大多数文献通过定性的方法来阐述多式联运的可靠性。汪芸芳等[1]通过对文献的梳理，发现可靠性是影响多式联运托运人偏好的重要因素之一。杨磊[2]引入可靠性构造多式联运绩效评价指标体系，但其可靠性指标仅通过每公里运输时间的总变异系数描述，并不能全面体现多式联运的可靠性。同时，在危险品多式联运和应急物资多式联运的相关研究中也涉及多式联运的可靠性，但一般仅适用于特殊环境。帅斌等[3]指出危险品多式联运可靠性评估模型存在系统性的不足，多集中于具体运输情况下的可靠性比较。李双琳等[4]将应急物资多式联运的可靠性转化为受灾点应急物资未满足的总损失最小。范厚明等[5]在多式联运节点选址模型中考虑路径可靠性，将路径失灵概率转化为惩罚费用。Zhang等[6]基于EOQ对海铁多式联运运行计划进行优化，并分析了海铁联运物流网络的可靠性指标、海铁联运网络的可靠性要求和海铁联运中连接的可靠性，提高了海铁集装箱多式联运的可靠性。多式联运系统与供应链系统、物流网络系统类似，也可参考其研究方式和方法。刘晶珩[7]基于三角模糊数层次分析法，从组织保障、流程柔性、信息系统3个维度构建应急供应链可靠性评价方法，并以S市的应急供应链进行实例进行了论证。任大勇[8]借助直觉模糊Petri网构建了可快速发现供应链系统中存在的关键薄弱要素的供应链可靠性诊断模型。Wu等[9]通过构建基于动态规划建模的敏捷供应链设计模型，探究了供应合作伙伴的数量和整个敏捷供应链的可靠性之间的权衡。白晓平等[10]利用贝叶斯-GO综合法发现收件子系统故障率最高，主要因素为快递员配送不及时、寄件损坏丢失。邓杨扬等[11]通过BP神经网络对构建的2级源于不确定性因素的制造业供应链可靠性评价模型进行求解，发现供应、生产、成员和成本4部分的不确定性对系统影响较大。任慧[12]通过改进的非支配排序遗传算法(NSGA-II)求解3级供应链网络设施选址与运输路径(LRP)模型，求解出以整个供应链网络的运营总成本最小和产品运输的可靠性最大为目标的最优运输路径。付红等[13]通过构建一对一供应链模型，分析了下游企业投资上游企业时对供应链可靠性和收益的影响。张亮星等[14]通过构建的多级串联可修复供应链系统模型，分析了供应链中制造企业正常工作和任一制造企业发生故障时供应链中制造企业的稳态值，并结合库存可靠性提出并验证了供应链可靠性的稳态可用度计算公式。Ozkan等[15]提出了一种基于蒙特卡罗(MC)模拟的物流与供应链网络(LaSCNs)可靠性评估方法，并通过多个案例验证了该算法的可行性和优势。Zhang等[16]透过建筑信息模型(BIM)与精益供应链(LSC)的整合模式，结合熵理论、集对分析(SPA)和马尔可夫链(EESM)，建立了一套评估BIM-LSC可靠性的方法。Wang等[17]采用蒙特卡罗模拟方法，结合需求增长、产量下降、炼油厂中断、管道中断等情景对需求侧管理的可靠性进行综合评估，建立了一种成品油供应链可靠性综合评价的系统方法。

综上所述，学者主要从显著影响可靠性的道路和人员方面进行研究，但较少考虑市场、政治、法律等外部因素，并且较少从定量的角度来研究多式联运网络的可靠度。本研究引入定量分析，分析多式联运中可靠性的关键影响因素，以期有助于工业企业制订大宗原材料采购及多式联运运输方案，同时有效地降低运营成本。

1 多式联运可靠性评价体系

1.1 多式联运可靠性评价指标体系的建立

通过对相关文献的梳理及相关企业的调研考察，将影响多式联运网络的因素的外部因素和内部因素组成。多式联运可靠性外部影响因素主要包括自然环境、经济环境、市场环境、政治环境、政策环境和法律环境等，内部影响因素主要包括交通环境、运输能力、设施设备、人员操作能力等，构建如表1所示的多式联运可靠性评价指标体系。

表1 多式联运可靠性评价指标体系Tab.1 Reliability evaluation indicator system of multimodal transport

1.2 多式联运可靠性故障树构建

故障树(Fault Tree，FT)是一种树状逻辑因果关系图，用来表示产品或系统发生某种故障与其组成部件或子系统故障之间的关系。通过系统的故障树分析，可找出目标系统发生故障的全部可能故障模式，并可定量计算出各故障模型的发生对目标系统可靠性影响的程度。建立多式联运系统故障树，将多式联运系统故障确定为顶事件T。根据多式联运可靠性评价指标体系确定出最基本的影响因素，作为故障树的底事件Xuv和Yuv，其他因素作为中间事件Xu和Yu。构建如图1所示的多式联运可靠性外部及内部影响因素故障树。

1.3 贝叶斯网络模型构建

依据构建的多式联运可靠性故障树，建立贝叶斯网络模型，多式联运可靠性(外部影响因素)故障树对应的贝叶斯网络模型，如图2(a)所示。

外部影响因素各节点的条件概率表示如下，其中0表示事件不发生，1表示事件发生,P(A|B)表示在事件B发生的情况下事件A发生的概率。

P(T1=1|X1=0,X2=0,X3=0,X4=0,X5=0,

X6=0)=0,

P(T1=1|其他)=1;

P(X1=1|X11=0,X12=0,X13=0)=0,

P(X1=1|其他)=1;

P(X2=1|X21=0)=0,

P(X2=1|其他)=1;

P(X3=1|X31=0)=0,

P(X3=1|其他)=1;

P(X4=1|X41=0)=0,

P(X4=1|其他)=1;

P(X5=1|X51=0,X52=0)=0,

P(X5=1|其他)=1;

P(X6=1|X61=0,X62=0)=0,

P(X6=1|其他)=1。

内部影响因素各节点的条件概率表示如下，其中0表示事件不发生，1表示事件发生。

P(T2=1|Y1=0,Y2=0,Y3=0,Y4=0)=0，

P(T2=1|其他)=1；

P(Y1=1|Y11=0,Y12=0)=0，

P(Y1=1|其他)=1；

P(Y2=1|Y21=0,Y22=0,Y23=0,

Y24=0,Y25=0)=0,

P(Y2=1|其他)=1;

P(Y3=1|Y31=0,Y32=0,Y33=0,

Y34=0,Y35=0)=0,

P(Y3=1|其他)=1;

P(Y4=1|Y41=0,Y42=0,Y43=0,

Y44=0,Y45=0)=0，

P(Y4=1|其他)=1。

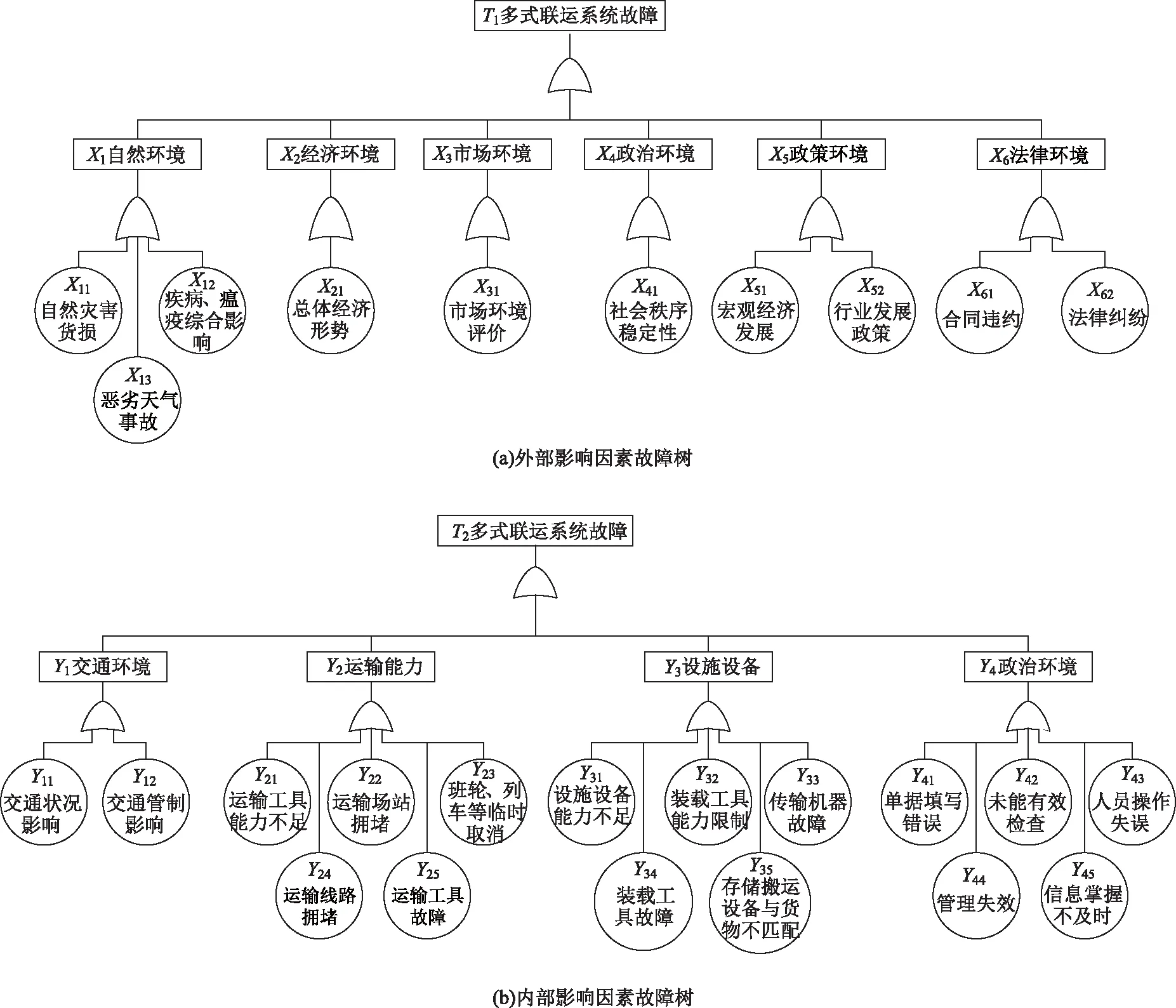
图1 多式联运可靠性影响因素故障树Fig.1 Fault trees of influences on multimodal reliability

图2 多式联运可靠性影响因素故障树对应的贝叶斯网络模型Fig.2 Bayesian network models corresponding to influencing factor fault tree of multimodal transport reliability

2 多式联运可靠性测度模型

2.1 底事件故障率计算模型

由于选取的风险因素较多，部分定性影响因素无法通过统计数据获得,因此采用模糊集理论对部分定性影响因素进行模糊评价，从而确定该影响因素的先验概率和条件概率分布。采用三角模糊数描述其故障率，其隶属度函数如下：

(1)

隶属函数图形如图3所示。

图3 三角模糊数的隶属函数图形Fig.3 membership function graph of triangular fuzzy numbers

选取的风险因素的历史数据较少，难以给出精确的表达，故引入7个自然语言变量：非常高、高、偏高、中等、偏低、低和非常低，这些自然语言变量可转换为相应的三角模糊数，其隶属函数图形如图4所示。

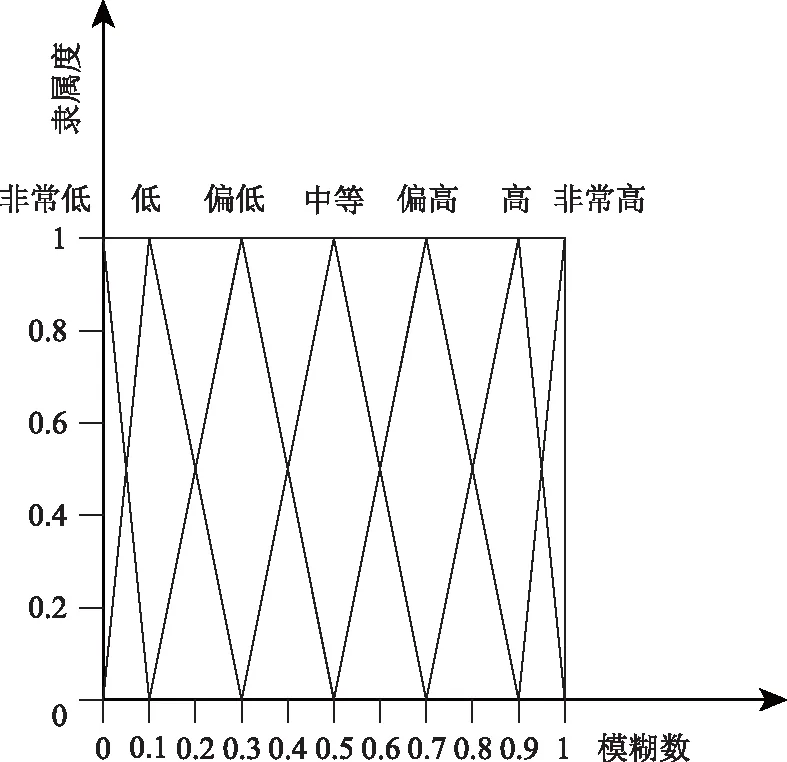
图4 各自然语言变量隶属度函数图Fig.4 Graph of membership function of each natural language variable

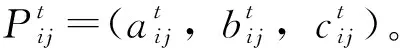
为得到相对贴近真实先验概率的模糊值，可将n位专家的评判意见取均值，得到该致险因素的模糊均值概率P′ij，即：

(2)

式中，a′ij和c′ij分别为n位专家对第i个因素处于风险等级j的评判意见的隶属度为0的上界和下界；b′ij为n位专家对第i个因素处于风险等级j的评判意见的隶属度为1时的模糊数。

采用面积均值法将模糊均值转化为最能代表该模糊集的概率，即：

(3)

将P′ij作归一化处理，求出该致险因素的先验概率及条件概率分布Pij，即：

(4)

式中k为该评价体系中共计k个风险等级。

2.2 多式联运可靠性计算模型

2.2.1 单个运输环节可靠性计算模型

依据贝叶斯网络基本理论，分别得到多式联运内外部影响因素的多式联运可靠性P(T1)，P(T2h)，P(T2r)，P(T2w),则多式联运系统的可靠性为：

P(Th)=αP(T1)+βP(T2h),α+β=1,

(5)

P(Tr)=αP(T1)+βP(T2r),α+β=1,

(6)

P(Tw)=αP(T1)+βP(T2w),α+β=1,

(7)

式中，P(T1)为多式联运外部影响因素可靠性；P(T2h)为多式联运内部影响因素(公路运输环节)可靠性；P(T2r)为多式联运内部影响因素(铁路运输环节)可靠性；P(T2w)为多式联运内部影响因素(水路运输环节)可靠性；P(Th)为多式联运公路运输环节可靠性；P(Tr)为多式联运铁路运输环节可靠性；P(Tw)为多式联运水路运输环节可靠性；α和β分别为外部影响因素和内部影响因素在评价系统可靠性时所占比例。

2.2.2 多式联运串联系统可靠性计算模型

多式联运串联系统即在多式联运过程中，货物从起点到终点仅有1条完整的可选择路径，货物在运输过程中不发生运量分配，作为一个整体从起点完整地运输到终点，中间不经过拆分和重组。多式联运串联系统示意图如图5所示。

图5 多式联运串联系统示意图Fig.5 Schematic diagram of multimodal transport series system

该系统的可靠性计算模型为：

(8)

2.2.3 多式联运并联系统可靠性计算模型

多式联运并联系统在多式联运运输过程中，由于各种运输方式存在运量限制，因此货物不一定作为一个整体从起点直接运输到终点，中间要考虑运量限制，存在运量拆分的问题。多式联运并联系统示意图如图6所示。

图6 多式联运并联系统示意图Fig.6 Schematic diagram of multimodal transport parallel system

该系统的可靠性计算模型为：

(9)

2.3 多式联运底事件重要度计算模型

重要度是指在顶事件发生的情况下，一个底事件对其产生影响的大小。贝叶斯网络中通常有多个底事件，而每个底事件是否发生对顶事件是否发生的作用是不一样的。有的底事件本身发生就可以导致顶事件发生，有的底事件需和其他底事件同时发生才能使顶事件发生，故分析系统中底事件的重要度对于识别引起系统故障的重要因素及系统的薄弱环节具有重要的作用。判断多式联运系统发生故障时，各个节点(基本事件)的后验概率可作为底层事件对顶事件的重要度，即后验概率代表各个事件对系统可靠性的影响程度。后验概率和先验概率并不是简单的对应关系，即节点的后验概率较大不一定代表节点的先验概率大，某个节点的后验概率大说明该节点对系统的可靠性的影响程度较大，是进行系统可靠性改进和预防的重要对象。各个节点(基本事件)的后验概率可由贝叶斯公式计算出，其含义表示在事件F发生的情况下，事件E发生的概率公式为：

(10)

式中，P(E)为事件E发生的概率，为先验概率且P(E)>0；P(F)为事件F发生的概率;P(E|F)为后验概率；P(F|E)为似然率。

3 算例分析

假设有1批物资需从防城港到某项目地，其间将经过南宁、百色、桂林、威舍、贵阳、宜宾、六盘水、大关、彝良、草海、昭通和水富港等12个节点，其多式联运网络图如图7所示。假设各节点间存在公路、铁路和水运3种运输方式，计算货物运输过程中的可靠性，取α=β=50%。

3.1 底事件故障率分析

根据多位多式联运行业专家学者、政府部门相关领导及企业负责人分别对影响因素X21，X31，X41的每种风险等级状态给出的评判意见，由图7和式(6)～(8)求出各影响因素的先验概率P(X21)=(0.310,0.655,0.052)，P(X31)=(0.322,0.638,0.061)，P(X41)=(0.333,0.617,0.05)。

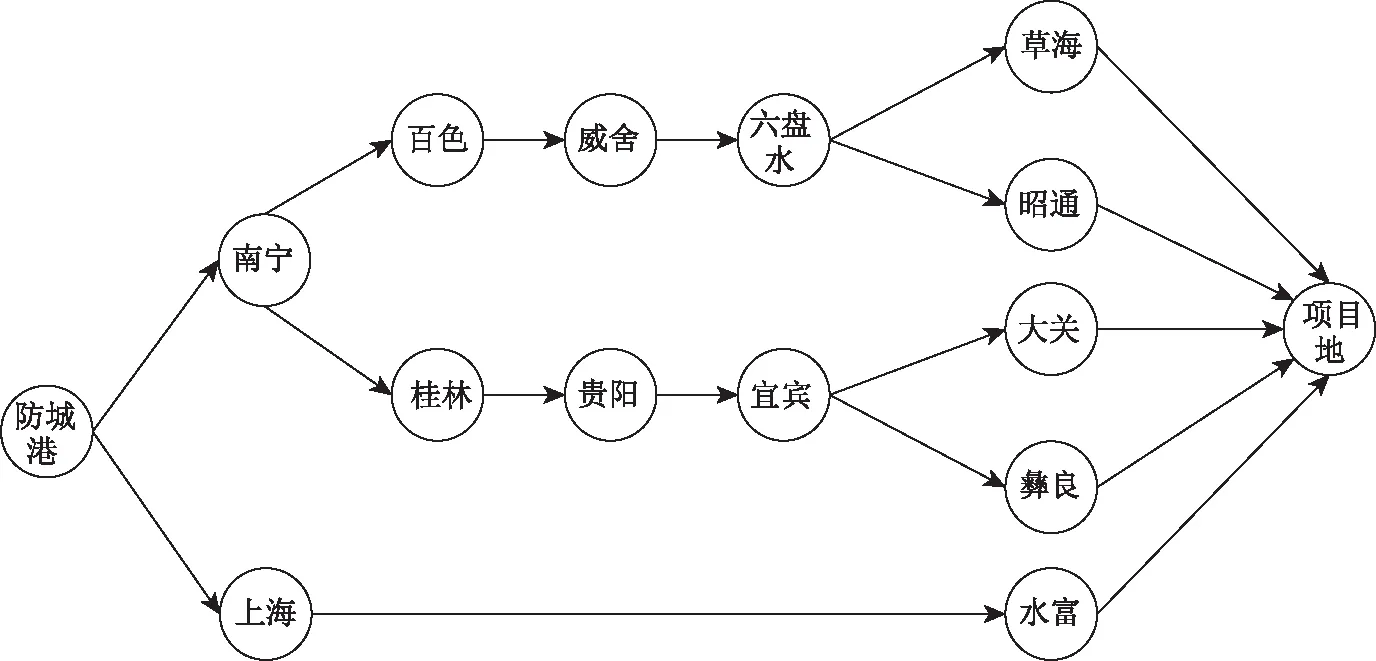
图7 多式联运网络Fig.7 Multimodal transport network

依据基本事件的界定[18]，并根据调研的资料，对相关文献中的基本事件的概率进行修正。表2至表3分别为多式联运外部和内部的影响因素的故障率列表。其中，内部因素中的交通环境和运输能力涉及公路、铁路、水运3种运输方式，由于3种运输方式的运输经济特点及适用条件不相同，因此这两者涉及的统一基本事件在不同的运输方式中发生故障的概率也不相同，其故障率如表4所示。

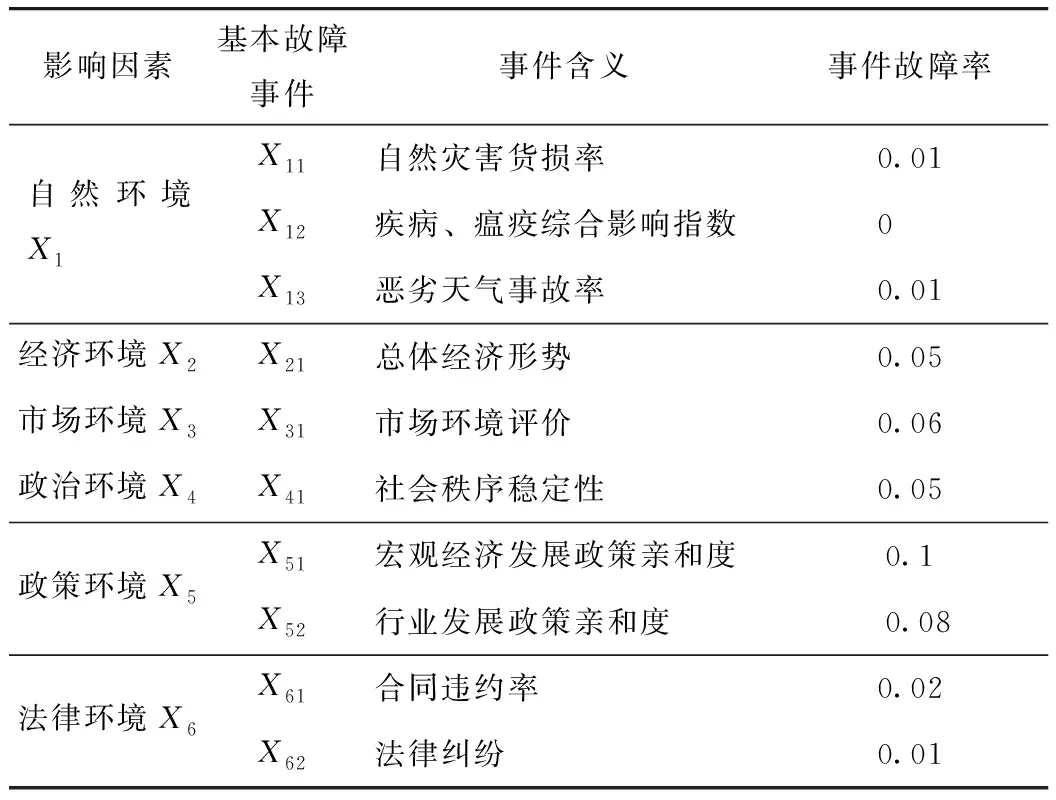
表2 多式联运外部影响因素基本事件故障率Tab.2 Failure rates of basic events of external influencing factors of multimodal transport

表3 多式联运内部影响因素基本事件故障率Tab.3 Failure rates of basic events of internal influencing factors of multimodal transport

表4 多式联运交通环境及运输能力影响因素基本事件故障率Tab.4 Basic event failure rates of multimodal transport environment and influencing factors of transport capacity

3.2 多式联运可靠性分析

3.2.1 多式联运内外部可靠性测算

(1)多式联运外部可靠性测算

根据表2得到的外部影响因素的基本事件故障率及图2(a)构建的贝叶斯网络模型，采用由Norsys公司开发的Netica软件对贝叶斯网络进行参数学习，最终得到多式联运外部影响因素导致的多式联运可靠性为P(T1)=81.2%。

(2)多式联运内部可靠性测算

公路运输环节：根据表3、表4得到的内部影响因素的基本事件故障率、公路运输基本事件故障率以及图2(b)构建的贝叶斯网络模型，对贝叶斯网络进行参数学习后最终得到多式联运内部影响因素(公路运输环节)导致的多式联运可靠性为P(T2h)=84.3%。

铁路运输环节：根据表3、表4得到的内部影响因素的基本事件故障率、铁路运输基本事件故障率以及图2(b)构建的贝叶斯网络模型，对贝叶斯网络进行参数学习后最终得到多式联运内部影响因素(铁路运输环节)导致的多式联运可靠性为P(T2r)=87.6%。

水路运输环节：根据表3、表4得到的内部影响因素的基本事件故障率、水路运输基本事件故障率以及图2(b)构建的贝叶斯网络模型，对贝叶斯网络进行参数学习后最终得到多式联运内部影响因素(水路运输环节)导致的多式联运可靠性为P(T2w)=79.4%。

3.2.2 单个运输环节可靠性测算

将α=β=50%代入式(5)～(7)得到下列结果。

多式联运可靠性(公路运输环节)：

P(Tk)=50%×81.2%+50%×84.3%=82.8%；

多式联运可靠性(铁路运输环节)：

P(Tr)=50%×81.2%+50%×87.6%=84.4%；

多式联运可靠性(水路运输环节)：

P(Tw)=50%×81.2%+50%×79.4%=80.3%。

3.2.3 多式联运串联系统可靠性测算

根据式(8)和每段路径的运输方式可靠性计算每条线路的可靠性，如表5所示。在串联系统中，引入铁路运输能有效提高系统可靠性；与之相反，引入水路运输将降低系统可靠性。

表5 多式联运串联系统可靠性Tab.5 Reliability of multimodal transport series system

3.2.4 多式联运并联系统可靠性分析

根据式(9)和每段路径的运输方式可靠性计算每条线路的可靠性，如表6所示。与串联系统相比，并联系统更为稳定，在多式联运中存在运量分配，当其中1条运输路径的可靠性得不到保证时，剩余的路径可保证运输的稳定。串联系统中所有货物仅有1条运输路径，但凡其中的任意环节出现故障便会阻断多式联运的正常运行。

表6 多式联运并联系统可靠性Tab.6 Reliability of multimodal transport parallel system

3.3 多式联运底事件重要度分析

依据各基本事件先验概率(事件故障率)和式(10)，利用MATLAB中的BNT工具箱计算其后验概率。

(1)外部影响因素

外部影响因素中有X1～X6共6个中间事件，X11～X62共10个相互独立的底事件。因各外部影响因素在不同运输方式下后验概率差异性较小，故在本研究中忽略不同运输方式对外部影响因素的影响。经MATLAB的BNT工具箱计算出的各底事件后验概率数值及与先验概率数值的对比，多式联运外部影响因素基本事件先验概率及后验概率如表7所示。

表7 多式联运外部影响因素基本事件先验概率及后验概率Tab.7 Prior probability and posterior probability of basic events of external influencing factors of multimodal transport

为了更直观体现多式联运外部影响因素基本事件的先验概率及后验概率，将表7转换成图8所示的多式联运外部影响因素基本事件先验概率及后验概率对比情况。

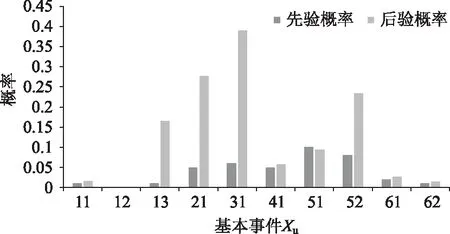
图8 多式联运外部影响因素基本事件先验概率及后验概率对比Fig.8 Comparison of prior probability and posterior probability of basic events of external influencing factors of multimodal transport

结果表明，在所有基本事件中，X13恶劣天气事故率、X21总体经济形势、X31市场环境评价和X52行业发展政策亲和度的后验概率较高，其中市场环境评价的后验概率最高，可见市场环境对多式联运的影响最大，其次是总体经济形势、行业发展政策亲和度和恶劣天气事故。因此尽量保障市场环境的稳定有序，总体经济形势的平稳发展，国家和地方政府应多推行有利于多式联运行业发展的政策，可有效提升多式联运的可靠性。

(2)内部影响因素

公路运输环节。公路运输环节中有Y1-Y4共4个中间事件，Y11-Y45共17个相互独立的底事件。经MATLAB的BNT工具箱计算出的各底事件后验概率的数值以及与先验概率的数值的对比，多式联运公路运输环节基本事件先验概率及后验概率如表8所示。

表8 多式联运公路运输环节基本事件先验概率及后验概率统计Tab.8 Statistics of prior probability and posterior probability of basic events in multimodal transport

同样，将表8转换成图9所示的多式联运公路运输环节基本事件先验概率及后验概率对比情况。

图9 多式联运公路运输环节基本事件先验概率及后验概率对比Fig.9 Comparison of prior probability and posterior probability of basic events in multimodal transport

对比结果，在所有基本事件中，Y11交通状况影响、Y12交通管制影响、Y21运载工具能力不足、Y24运输线路拥堵和Y43人员操作错误的后验概率较高，其中运输线路拥堵的后验概率最高，由此可见运输线路不足是多式联运公路运输环节的薄弱环节，其次是运载工具能力不足、交通管制影响、交通状况影响和人员操作错误，因此在公路运输环节中，多式联运承运人应根据公路运输的实际情况选择运输方式。

铁路运输环节。铁路运输环节中有Y1-Y4共4个中间事件，Y11-Y45共17个相互独立的底事件。经MATLAB的BNT工具箱计算出的各底事件后验概率数值及与先验概率数值的对比。多式联运铁路运输环节基本事件先验概率及后验概率如表9所示，多式联运铁路运输环节基本事件先验概率及后验概率对比情况如图10所示。

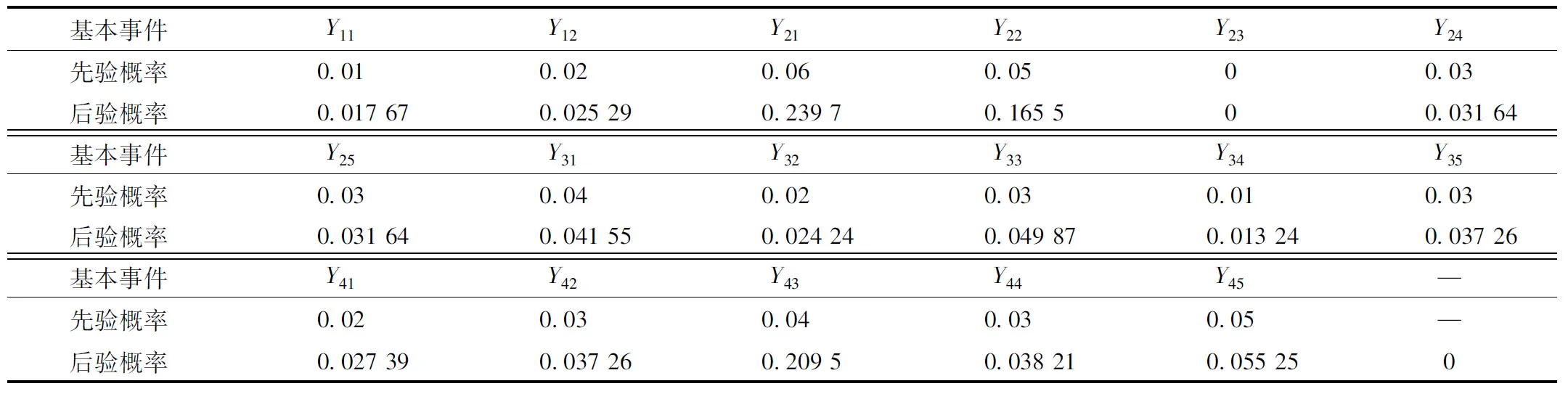
表9 多式联运铁路运输环节基本事件先验概率及后验概率统计表Tab.9 Statistics of prior probability and posterior probability of basic events of railway transport in multimodal transport

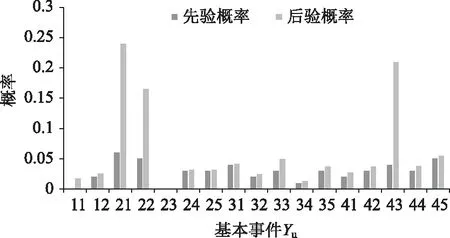
图10 多式联运铁路运输环节基本事件先验概率及后验概率对比情况Fig.10 Comparison of prior probability and posterior probability of basic events of railway transport in multimodal transport

对比结果，在所有基本事件中，Y21运载工具能力不足、Y22运输场站拥堵和Y23人员操作错误的后验概率较高，其中运载工具能力不足的后验概率最高，由此可见运载工具能力不足是多式联运铁路运输环节的薄弱环节，其次是人员操作错误和运输场站拥堵，铁路运输中常因为铁路运力不足造成货物滞留，因此在铁路运输环节中，多式联运承运人应根据承运货物的重量进行恰当的选择。

水路运输环节。水路运输环节中Y1-Y4共4个中间事件，Y11-Y45共17个相互独立的底事件。经MATLAB的BNT工具箱计算出的各底事件后验概率数值及与先验概率数值的对比。多式联运水路运输环节基本事件先验概率及后验概率如表10所示，多式联运水路运输环节基本事件先验概率及后验概率对比情况图11所示。

表10 多式联运水路运输环节基本事件先验概率及后验概率统计Tab.10 Statistics of prior probability and posterior probability of basic events of waterway transport in multimodal transport

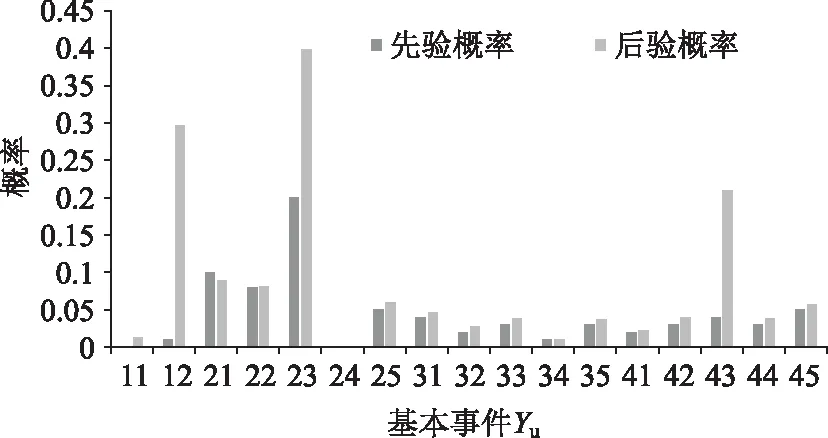
图11 多式联运水路运输环节基本事件先验概率及后验概率对比情况Fig.11 Comparison of prior probability and posterior probability of basic events of waterway transport in multimodal transport

对比结果，在所有基本事件中，Y23班轮、列车等临时取消、Y12交通管制影响和Y43人员操作失误的后验概率较高，其中班轮、列车等临时取消的后验概率最高，由此可见班轮的临时取消是多式联运水路运输环节中的薄弱环节，其次是交通管制影响和人员操作失误，因此水路运输环节中，多式联运承运人应根据货物的需求选择合理的运输方式，如若货物对时间需求较为迫切则不适合选择水路运输。同时，应对相应的人员进行更为细致的培训，避免操作失误的产生进而影响多式联运运输。

4 结论

从内部和外部因素2方面构建多式联运可靠性测度指标体系，应用故障树、贝叶斯网络等方法，计算多式联运网络的可靠性及各因素影响的重要度，得出以下结论：

(1)各运输方式的可靠性存在差异。其中铁路运输的可靠性最高，公路运输的可靠性次之，水路运输的可靠性最低。路径中水路运输越多，路径的整体可靠性越低。

(2)多式联运并联系统的可靠性要高于串联系统的可靠性，并且随着并联系统运量分配次数的增加，多式联运的可靠性逐渐升高。并联系统中有多条并联的运输路径保障系统可靠性。而串联系统中仅有1条运输路径，当任意环节出现故障则会阻断多式联运的正常运行。

(3)外部影响因素中，市场环境对多式联运的影响最大，其次是总体经济形势、行业发展政策亲和度和恶劣天气事故。政府部门应制定激励政策，营造良好的运营环境，促进多式联运发展。同时，企业也应制订灾害天气应急预案，确保多式联运安全。

(4)内部影响因素中，不同运输方式的薄弱环节不同。公路运输中，运输线路不足是其最薄弱的环节；铁路运输中，运载工具能力有限是其最薄弱的环节；水路运输中，班轮的临时取消是其最薄弱的环节。企业可通过建设网络平台提前规划多条备选运输路线，或对路线上发生的突发事件及时响应并规划出新的路线等措施来降低公路运输风险。企业可以通过优化铁路运输计划来提高运载能力。