实心圆柱桥墩防车撞装置的防撞性能对比分析

王向阳，张林凯,2

(1.武汉理工大学 交通与物流工程学院，湖北 武汉 430063;2. 中信建筑设计研究总院有限公司，湖北 武汉 430014)

0 引言

中国拥有超过100万座公路和铁路桥梁，是名副其实的“桥梁大国”。近年来桥梁建设的发展，也带来很多安全问题，桥梁防车撞就是其中之一。目前，中国对于车桥碰撞及防撞装置的研究尚处于起步阶段，相关规范也不完善，因此对车桥碰撞和防撞装置研究很有必要。

泡沫铝材料是一种以铝金属为骨架的新型结构材料，同时具有金属和气泡的特性。近年来，泡沫铝凭借质量轻，吸能效率高等优点，被大量地应用于制造缓冲装置、减震装置以及保险杠等安全装置上。徐东丰[1]分析了汽车撞击带有泡沫铝防护装置桥墩的外部动力响应问题，证明了泡沫铝防护装置对桥墩可以起到保护作用。

橡胶混凝土作为一种新型的骨料混凝土，可以吸收大量能量,而并不改变混凝土中各组成材料的化学性能[2]。李伟龙[3]设计了一种橡胶混凝土覆层作为桥梁的防撞结构，证明了采用橡胶混凝土材料作为防撞层是可行的。

许多学者对于用不同材料组合的装置进行了研究[4-6]。胥睿[7]对钢板-橡胶混凝土复合覆层应用于桥墩防撞做了介绍；唐进元[8]设计了一种基于泡沫铝“三明治”结构的新型斜井跑车防护装置，采用铝合金材料作为夹层板，分析其吸能特性和可能的失效形式；刘海证[9]研究了泡沫铝外包混凝土桥墩的防撞性能，证明其能对车辆桥墩都起到很好的保护作用。

本研究研究不同材料的附着式防撞装置对桥墩防撞性能的影响，设计一种泡沫铝外包橡胶混凝土防撞装置，其综合了泡沫铝和橡胶混凝土各自的优点，泡沫铝材料可以吸收较多的能量，橡胶混凝土可以产生较小的撞深，并将该装置与泡沫铝防撞装置和橡胶混凝土防撞装置进行对比，通过能量转化、撞击力大小和装置撞深等方面来研究装置的防撞性能，为桥墩防车撞研究和设计等提供依据。

1 防撞装置及其有限元模拟

1.1 项目背景

以某30 m连续梁桥为研究对象，桥墩为双柱式实体圆柱墩，桥墩直径为1.5 m，高7 m，采用C30混凝土，纵筋为HRB400钢筋。对该桥墩设立防撞装置后，采用ANSYS有限元软件分析车辆撞击该桥墩的动力响应。

(1)车辆模型

车辆模型参考了一辆Ford800卡车模型[10-11]，车辆模型主要由车头、保险杠、车架、车厢等部位组成，其相关材料参数如表1所示。

表1 车辆各部位材料参数Tab.1 Material parameters for each part of vehicle

碰撞时车头与保险杠变形较大，因此还需要考虑材料的失效和应变率，采用Cowper-Symonds模型来模拟，其屈服应力公式如下：

(1)

车厢采用刚性体模拟，通过改变车厢的壳单元厚度来模拟不同质量的车辆。

(2)桥墩模型

桥墩采用SOLID164实体单元模拟，混凝土等级为C30，材料本构模型选用在高速碰撞领域中运用较多的HJC损伤本构模型。桥墩具体尺寸和材料参数等见文献[12-13]。

1.2 防撞装置设计

3种防撞装置均为圆筒状，以桥墩覆层的形式附着在桥墩表面，即内径与桥墩直径相同为1.5 m，外径为2.1 m，厚度均为0.3 m，高度均为2.5 m。泡沫铝防撞装置采用显式SOLID164单元模拟，泡沫铝材料选用LS-DYNA材料库中的MAT-63号可压缩泡沫材料模型(关键字为MAT-CRUSHABLE-FOAM)模拟[8]。橡胶混凝土防撞装置采用HJC本构模型模拟，参考李伟龙[3]的橡胶混凝土材料静力力学性能试验及拉压滞回试验确定橡胶混凝土材料模型的计算参数。泡沫铝外包橡胶混凝土防撞装置是由泡沫铝和橡胶混凝土按一定的结构形式组合的装置，根据刘海证[9]泡沫铝外包混凝土的防撞装置，将外包的C30混凝土替换成橡胶混凝土材料，采用0.2 m厚的泡沫铝材料并外包0.1 m的橡胶混凝土材料，各相关材料参数取值见文献[13-14]。

1.3 有限元建模

(1)接触定义及参数设置

将车辆与桥墩、车辆与防撞装置和防撞装置与桥墩直接的接触设置为面面接触中的自动接触(ASTS)，车辆和防撞装置自身内部的接触都设置为自接触(ASSC)。自动接触中需要定义静摩擦系数和动摩擦系数，本研究采用李伟然[15]在车-桥墩防撞装置数值模拟时采用的参数，设置静摩擦系数为0.3，动摩擦系数为0.2。

(2)沙漏能及滑移界面能的控制

沙漏能的产生是因为LS-DYNA程序为了减少CPU的计算时间，采用单点缩减积分进行计算，进而激起零能模式，导致单元没有刚度，变形呈现锯齿形网格，它的出现容易导致结果无效，需要避免这种模式，或者尽量减小零能模式。仿真分析中滑移界面能属于非物理量，也需要对其进行控制。一般地，沙漏能和界面滑移能之和不超过总能量的10%，可以认为分析结果是可靠的[16]。

(3)时间步长的控制

显式积分算法只有在特定条件下才能使求解过程趋于稳定。时间步长Δt均要小于临界时间步长Δtcr，Δtcr取决于模型中网格的最小单元尺寸，这样计算结果才能收敛。本研究取计算时间步长为0.002 s，总计算时间为0.2 s。

(4)单元网格划分

本研究有限元模型，将车辆模型中车头和保险杠部分的单元尺度设为2 cm，车架部分的单元尺度设为5 cm，车厢部分单元尺度设为10 cm；桥墩和防撞装置模型的单元尺度均为10 cm。

(5)边界条件的定义

研究表明[17]，墩顶自由与墩顶固结时的最大撞击力误差仅为7%，桥梁上部结构对墩顶的约束作用，采用COMBI165弹簧单元来模拟，计算表明其与全桥模拟时桥墩所受最大撞击力几乎不变。车辆撞击桥墩时，其碰撞持续时间极短，且桥墩所受撞击力较大，因此将桥墩墩底与地面刚性连接，建模时将墩底节点的自由度全部约束。

建立的有限元模型如图1、图2所示。

图1 车辆与桥墩碰撞有限元模型Fig.1 Finite element model of vehicle-bridge pier collision

图2 车-防撞装置-桥墩碰撞有限元模型Fig.2 Finite element model of vehicle + anti-collision device + pier

1.4 有限元建模合理性分析

由于没有试验数据验证有限元建模的正确性，为验证有限元模型的合理性，从系统的能量角度出发，数值仿真过程中能量转化和能量守恒可以作为判断有限元模型是否正确合理的一个重要标准[18]。

将桥梁上部结构对墩顶的作用简化为竖向荷载作用，将上部结构重量平均分给每一个桥墩，得到桥墩所受竖向荷载P=2.8 MPa(采用竖向面荷载作用在桥墩顶面)。对比有、无竖向荷载作用下桥墩所受的最大撞击力和位移，结果如表2所示。

表2 不同竖向荷载下桥墩的动力响应值(m=8 t，v=80 km/h)Tab.2 Dynamic response values of bridge piers under different vertical loads (m=8 t,v=80 km/h)

从表2可以看出，竖向荷载作用下，桥墩所受最大撞击力峰值基本不变，且撞击力峰值出现的时间一致，但增加竖向荷载会减小墩顶的最大位移，受撞区最大位移基本一致。因此，是否施加上部荷载对桥墩最大撞击力影响不大，且在之后的研究主要考虑受撞区的位移，在后面的研究中将不考虑上部结构对桥墩的竖向荷载作用。

整个碰撞过程中，车辆以某一速度与桥墩碰撞，车头先与桥墩发生碰撞产生变形，撞击力达到第1个峰值，然后迅速下降，随后车厢与桥墩2次碰撞使撞击力再次上升产生第2个峰值，之后撞击力缓慢下降直到为0。图3为8 t的卡车以80 km/h的速度撞击无防撞装置时的桥墩的撞击力时程图。

图3 车辆与裸墩碰撞时撞击力时程(m=8 t，v=80 km/h)Fig.3 Time history of impact force during collision between vehicle and bare pier (m=8 t,v=80 km/h)

采用车重为8 t的卡车以80 km/h的速度分别与带有泡沫铝防撞装置、橡胶混凝土防撞装置和泡沫铝外包橡胶混凝土防撞装置的桥墩进行正面对中碰撞模拟，观察整个模型的能量传递与变化，来验证有限元模型的正确性。

图4是车-防撞装置-桥墩碰撞时的能量变化时程图，从图4可以看出：车重为8 t的卡车以80 km/h 的速度撞击3种防撞装置的总能量为1.96×106J，碰撞结束后3种工况的剩余动能分别为1.23×105J,1.02×105J,1.17×105J，分别占总能量的6.3%,5.2%,6.0%；系统内能分别为1.79×106J,1.82×106J,1.80×106J，分别占总能量的91.3%,92.9%,91.8%；界面滑移能分别为4.35×104J,3.53×104J,4.39×104J，分别占总能量的2.2%,1.8%,2.2%，本研究采用全积分的方式使沙漏能始终为0，计算结果中总能量基本等于动能与内能之和，沙漏能和界面滑移能之和不超过总能量的10%，说明沙漏能和界面滑移能控制满足条件，计算结果满足有限元仿真计算要求[11]，验证了上述3种防撞装置有限元模型的合理性。

图4 车-防撞装置-桥墩碰撞能量时程Fig.4 Energy time histories of vehicle + anti-collision device + pier collision

从整个系统的动能时程曲线可以看出，碰撞过程中，车辆的动能逐渐转化为防撞装置和桥墩的内能，小部分转化为接触界面的滑移能，动能减小的速度随时间变小，这是因为碰撞开始后防撞装置产生变形，吸收大部分动能，随着时间的增加其变形逐渐达到最大值，随后动能有小幅度上升，是因为防撞装置的弹性变形和桥墩的阻滞作用，出现了速度反弹，但回弹速度非常小，最后趋于稳定。系统的内能和动能曲线变化趋势几乎相反，符合实际碰撞过程变化规律。

2 碰撞分析及计算

2.1 车辆碰撞对桥墩动力响应的影响

用质量为16 t的车辆以80 km/h的速度对上述桥墩(无防撞装置)进行正面对中碰撞，以该典型工况为例，对车桥碰撞过程中桥墩结构的位移、应力等进行分析。

(1)位移分析

图5～图6分别反映了碰撞过程中受撞区域和墩顶的位移时程图。可以看到无论是撞击区域还是墩顶，整个车桥碰撞过程桥墩的位移变形都呈周期性的增长与回落，最后趋于稳定，符合一般车桥碰撞过程。结合图3可知，当0.15 s后撞击力基本为0，但桥墩仍然有位移变形，说明桥墩内部可能已经产生了一定的塑形变形。

图5 受撞区位移时程图Fig.5 Time history of displacement in impacted area

图6 墩顶位移时程图Fig.6 Time history of pier top displacement

(2)应力分析

通过分析车桥碰撞后桥墩结构内部的应力响应可以一定程度上反应桥梁结构是否安全可靠，在车桥碰撞过程中会产生各类应力，其中等效应力是基于剪切应变能的一种应力，当单元体的形状改变比能达到一定程度，材料开始屈服，它可以直观地反映出桥墩各节点的应力状态，从而快速确定模型中的最危险区域。

图7反映不同时刻桥墩的等效应力云图。从图7可以看到：碰撞刚开始时撞击区域内的应力迅速上升且向四周发散，应力上升到最大值后开始出现周期性的上升与下降，但总体上应力在逐渐减小。撞击区域内的应力发展过程符合车桥碰撞时撞击力时程曲线变化规律，最后撞击力为0后桥墩等效应力趋于一个稳定值。

图7 不同时刻桥墩的等效应力云图(单位：Pa)Fig.7 Nephograms of equivalent stress on bridge pier at different moments(unit:Pa)

从图7明显看到桥墩大部分区域所受的等效应力值(t=0.04 s时最大应力为39.7×106Pa，t=0.145 s时为33.7×106Pa)大于C30混凝土轴心抗压强度标准值20.1×106Pa，且撞击区域内节点的应力超过标准值较多，其次是墩底区域，说明车桥碰撞过程中撞击区域容易出现压溃破坏，应力损伤的区域主要为撞击区域，其次是墩底区域。证明了车桥碰撞事故会导致桥墩出现损伤和破坏，建立相应的防撞装置是有必要的。

增设泡沫铝防撞装置，其余初始条件不变，有限元分析结果发现：应力发展规律基本与裸墩时一致，当t=0.038 s时，桥墩所受最大等效应力为16.02×106Pa，小于C30混凝土轴心抗压强度标准值20.1×106Pa。说明防撞装置的增加并不改变应力发展规律，但能使桥墩承受该车辆撞击，满足抗压强度要求。经计算，增设30 cm橡胶混凝土防撞装置和泡沫铝外包橡胶混凝土防撞装置均能使桥墩满足抗压强度要求，在此不一一赘述。

图8 t=0.038 s时桥墩所受等效应力云图(单位：Pa)Fig.8 Nephogram of equivalent stress on bridge pier at t=0.038 s(unit:Pa)

2.2 碰撞工况设计

车桥碰撞时有很多不确定因素，本研究主要考虑车辆的质量、撞击速度以及车辆纵轴线与桥墩轴心间的偏心距距离，对防撞装置防撞性能研究提供参考。

车辆质量为8,12 和16 t，来模拟车辆空载、满载和超载的情况；车辆的撞击速度为20,40,60 和80 km/h；车辆与桥墩碰撞的偏心距为0，0.3，0.6和0.9 m。每种初始条件下的车辆分别与裸墩和带有3种防撞装置的桥墩发生碰撞，对桥墩所受撞击力、装置吸能和撞深等进行研究。

2.3 碰撞结果分析

(1)速度因素对防撞装置的影响

质量为8 t的车辆分别以20，40，60和80 km/h正面碰撞桥墩和3种防撞装置，计算结果如表3所示。

表3 不同速度下车桥碰撞计算结果Tab.3 Calculation result of vehicle-bridge collision at different speeds

从表3可以看出，在4种速度下，3种防撞装置的撞击力折减率最大的是泡沫铝防撞装置，相应的也有最长的撞击持续时间，但其有最大的装置塑性撞深，撞击力折减率最小的是橡胶混凝土防撞装置，响应的也有最短的撞击持续时间，但其有最小的装置塑性撞深，泡沫铝外包橡胶混凝土防撞装置的各项指标均介于上述两种防撞装置之间。这种情况在低速碰撞时更为明显，以20 km/h为例，泡沫铝外包橡胶混凝土防撞装置撞击力折减率和泡沫铝防撞装置相差0.3%，但其塑性撞深却减小了41.0%(8.2 mm)。高速碰撞时，以80 km/h为例，泡沫铝外包橡胶混凝土防撞装置撞击力折减率和泡沫铝防撞装置相差5.3%，但其塑性撞深却减小了25.0%(19.5 mm)。

与橡胶混凝土防撞装置相比，泡沫铝外包橡胶混凝土防撞装置虽然塑性撞深较大，但其撞击持续时间较长，这和装置结构的刚度有关，说明橡胶混凝土防撞装置刚度较大，不容易产生变形，刚度过大有可能对车辆造成极大的破坏，因此泡沫铝外包橡胶混凝土防撞装置是一种良好的缓冲吸能防撞装置。

从图9可以看出，随着车辆速度的增大，撞击初始动能相应增加，使得桥墩所受撞击力峰值增大，撞击持续时间也增加。桥墩加设防撞装置后，其撞击力峰值均有不同程度的减小，由于防撞装置的缓冲吸能作用，撞击持续时间也相应增加。从图10可以看出，随着车辆速度的增大，防撞装置的塑性撞深也越来越大，泡沫铝防撞装置和泡沫铝外包橡胶混凝土防撞装置变化幅度较大，橡胶混凝土防撞装置变化幅度明显小于上面两种防撞装置，当速度超过60 km/h后装置的塑性撞深基本不变，说明橡胶混凝土防撞装置变形已经趋于极限，高速碰撞下不利于变形吸能。

图9 不同速度下最大撞击力峰值Fig.9 Maximum peak impact forces at different speeds

图10 不同速度下的装置塑性撞深Fig.10 Plastic penetration depths of device at different speeds

(2)质量因素对防撞装置的影响

质量为8，12和16 t的车辆以80 km/h正面碰撞桥墩和3种防撞装置，计算结果如表4所示。

表4 不同质量车辆车桥碰撞计算结果Tab.4 Calculation result of vehicle-bridge collision with different vehicle masses

从图11、图12可知，车辆质量增加，第1撞击力增加不明显，但会显著增加第2撞击力峰值，此时已经出现了明显的第2撞击力峰值，但均小于第1撞击力峰值；从图13看出泡沫铝防撞装置和泡沫铝外包橡胶混凝土防撞装置塑性撞深随着车辆质量的增加而增大，尤其在高质量下增加更明显，但橡胶混凝土防撞装置塑性撞深基本不变，可以认为其已经吸收了最大的能量。同时，表4指出随着车辆质量的增加，无论有无防撞装置，其撞击持续时间显著增加。这说明质量的增加虽然不能增加第1撞击力峰值，但增加了碰撞持续时间，这是因为车厢二次碰撞的动量增大，使得二次碰撞的时间也增加。

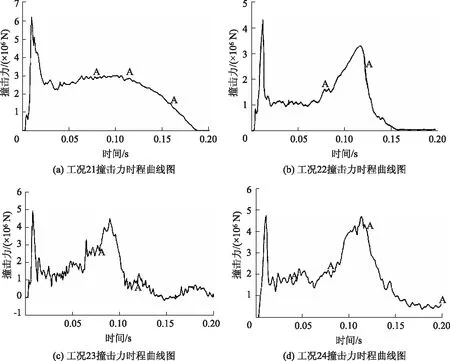
图11 车辆撞击力时程曲线Fig.11 Time history curves of vehicle impact force

图12 不同质量下最大撞击力峰值Fig.12 Maximum peak impact forces with different masses

图13 不同质量下的装置塑性撞深Fig.13 Plastic penetration depths of the device with different masses

比对结果数据可知，泡沫铝防撞装置缓冲吸能效果最好，泡沫铝外包橡胶混凝土防撞装置次之，橡胶混凝土防撞装置缓冲吸能效果最差，其装置刚度最大，可能会在高质量车辆碰撞时使得车辆损坏更加严重。

(3)偏心距因素对防撞装置的影响

8 t的车辆以80 km/h的速度，分别以偏心距为0(正面碰撞)，0.3，0.6和0.9 m，碰撞桥墩和3种防撞装置，计算结果见表5、图14和图15。

表5 不同偏心距车桥碰撞计算结果Tab.5 Calculation result of vehicle-bridge collision with different eccentricities

图14 不同偏心距时最大撞击力峰值Fig.14 Maximum peak impact forces with different eccentricities

图15 不同偏心距的装置塑性撞深Fig.15 Plastic penetration depths of device with different eccentricities

由计算结果可知，桥墩所受撞击力随偏心距的增大而减小，但撞击持续时间会随偏心距增大而增大，因车辆偏心碰撞防撞装置，撞击过程中车头仅有一侧碰撞变形，仍具有较大的动能继续向前移动，导致防撞装置的塑性撞深会比正撞时要大，从图14可以看出，偏心碰撞下防撞装置的塑性撞深随偏心距的增大呈现先增加后减小的趋势，且泡沫铝防撞装置和泡沫铝外包橡胶混凝土防撞装置的塑性撞深远大于橡胶混凝土防撞装置的塑性撞深。泡沫铝防撞装置和泡沫铝外包橡胶混凝土防撞装置在偏心距为0.3 m时有最大的塑性撞深，分别为148.0 mm和107.0 mm，橡胶混凝土防撞装置在偏心距为0.6 m时有最大的塑性撞深18.7 mm。这说明在偏心碰撞情况下，防撞装置的撞深会比正面碰撞时要大，具体哪个角度的偏心碰撞下对防撞装置的撞深影响最大，还应进行进一步研究。

2.4 装置防撞性能对比

选取8 t车辆以80 km/h的速度正撞对应的桥墩和防撞装置(工况13～16)，研究装置的防撞性能。由上文计算结果可知，工况13～工况16下桥墩所受撞击力峰值分别为6 175，4 389，4 866和4 717 kN，工况14，15和16相比工况13撞击力峰值折减了28.9%，21.2%和23.6%，泡沫铝防撞装置折减的撞击力最大，橡胶混凝土防撞装置折减的撞击力最小，泡沫铝外包橡胶混凝土防撞装置折减率介于两者之间。无防撞装置下，整个碰撞过程持续了0.109 s，带有泡沫铝防撞装置时碰撞过程持续了0.156 s，带有橡胶混凝土防撞装置时碰撞过程持续了0.121 s，带有泡沫铝外包橡胶混凝土防撞装置时碰撞过程持续了0.147 s。可以看到，设置防撞装置后，相比裸墩碰撞情况，桥墩所受的撞击力有明显的减少，且撞击持续时间相应增加，防撞装置通过自身的变形吸能吸收了车辆撞击时产生的能量，使得桥墩所受内能减小，有利于保护桥墩不受破坏，进而保护桥梁整体的安全性。

图16 防撞装置内能时程曲线图Fig.16 Time history curves of internal energy of anti-collision device

图17 防撞装置撞深时程曲线图Fig.17 Time history curves of penetration depth of anti-collision device

图16、图17分别表示碰撞过程中防撞装置内能及撞深时程曲线。泡沫铝防撞装置最终吸收的能量为2.23×105J，最大撞深为88.2 mm，最终塑性撞深为78.1 mm，橡胶混凝土防撞装置最终吸收的能量为6.92×104J，最大撞深为15.0 mm，最终塑性撞深为11.5 mm，泡沫铝外包橡胶混凝土防撞装置最终吸收的能量为2.07×105J，最大撞深为62.7 mm，最终塑性撞深为58.6 mm。可以看到由于车辆速度进一步增加，防撞装置吸收的能量和防撞的撞深都相应增加，泡沫铝防撞装置吸收的能量最大，橡胶混凝土防撞装置吸收的能量最小，泡沫铝外包橡胶混凝土防撞装置吸能效果介于两者之间，但和泡沫铝吸能效果差距不大。此外，防撞装置的结构刚度与撞深呈负相关，即在保证撞击力满足规范要求的前提下，防撞装置的结构刚度与其撞深成反比，因此，可以看出泡沫铝防撞装置的结构刚度最小，橡胶混凝土防撞装置结构刚度最大，而泡沫铝外包橡胶混凝土结构刚度介于两者之间，说明泡沫铝外包橡胶混凝土防撞装置兼具两种材料的特性，不仅可以吸收大量能量，且不会产生较大的装置变形值。

采用无量纲化分析研究3种装置的防撞能力。选取工况14～16进行分析，3种防撞装置的质量分别为754.94，9 754.88和4 088.15 kg。3种装置单位质量下的撞击力折减率比值、塑性撞深比值和装置吸能比值(假定泡沫铝装置的各比值为100%)见图18。显示单位质量泡沫铝的撞击力折减率、塑性撞深、装置吸能比都远远高于另外两种装置。而单位质量橡胶混凝土装置的3种比值都最小。如果桥梁性能对桥墩质量增加比较敏感，可以优先考虑泡沫铝装置防撞。

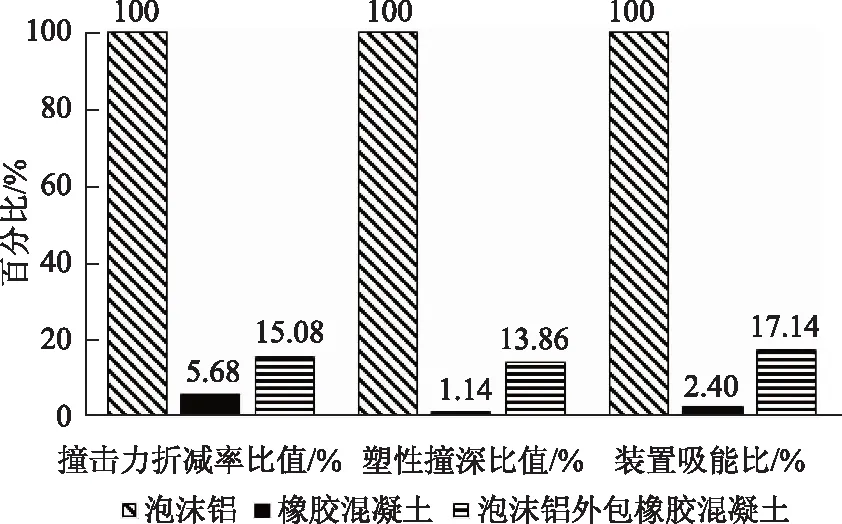
图18 单位质量下3种装置的防撞性能无量纲化比较Fig.18 Dimensionless comparison of anti-collision performance of 3 devices per unit mass

3 结论

(1)防撞装置的结构刚度与其撞深成反比，其中泡沫铝防撞装置结构刚度最小，泡沫铝外包橡胶混凝土防撞装置次之，橡胶混凝土防撞装置结构刚度最大，选择适当刚度的防撞装置有利于保护驾驶人的生命安全及装置的重复利用和维修。

(2)桥墩所受撞击力峰值随车辆速度增大而增大，车辆质量的增加对第1撞击力峰值的影响不明显，但显著提高了撞击持续时间和第2撞击峰值，撞击力随偏心距的增大而减小，撞击持续时间会随偏心距增大而增大。

(3)防撞装置的塑性撞深随车辆速度、车辆质量的增大而增加，随偏心距的增大呈现先增加后减小的趋势。

(4)泡沫铝防撞装置撞击力折减率最大，橡胶混凝土防撞装置的塑性撞深最小，撞击持续时间最短。泡沫铝外包橡胶混凝土防撞装置综合了泡沫铝和橡胶混凝土两种材料的性能，不仅可以吸收较多的能量，而且可以产生较小的塑性撞深，是一种很好的新型缓冲吸能防撞装置。

(5)无量纲化分析结果表明，如果桥梁性能对桥墩质量增加比较敏感，可以优先考虑泡沫铝装置防撞。