信号交叉口相位间谈判博弈协调控制
夏新海,许伦辉,杨景山,彭智敏
(1.广州航海学院 港口与航运管理学院,广东 广州 510725;2.华南理工大学 土木与交通学院,广东 广州 510640;3.广州航海学院 土木与工程管理学院,广东 广州 510725;4.广州大学 机械与电子工程学院 广东 广州 510006)
0 引言
交叉口是城市路网中各向交通流汇聚交错的地点,对它的交通信号控制是城市交通控制系统的核心,并且是实现干道和区域交通信号协调控制系统的基础。要实现未来城市交通信号控制的智慧化,交叉口交通信号控制显得极为重要[1]。交叉口交通信号控制用到的Webster方法、冲突点法等方法难以适应交通条件发生的变化。常规感应控制没有考虑到相位之间的矛盾,增加绿灯时间可能会造成其他相位平均车辆排队长度增大。虽然SCOOT,SCATS,OPAC等自适应交通信号控制系统比固定交通信号控制和感应式交通信号控制方案的性能要好,但其往往在可扩展性和鲁棒性等方面受到限制。近10年来神经模糊网络、tabu搜索、自组织协调图、情感算法、遗传算法等方法用来改进交叉口交通信号控制方案,但存在指数复杂性和需要大量数据来校准参数等局限性。
博弈论是研究理性决策者之间策略交互的数学模型,其被认为是解决城市交通信号控制问题的合适方法,有利于提高协调控制效率,能较好地适应交通需求水平的动态变化[2-4]。早期,一些学者(如Villalobos 等[5],杨晓芳等[6],朱铭琳等[7],李建明等[8],Clempner 等[9])使用非合作博弈来进行交叉口相位交通信号协调控制,并取得了一定的效果。但非合作博弈各参与者没有交互动作等信息,其纳什均衡缺乏对效率的考虑,并容易陷入局部最优解,协调效率有限。Elhenawy等[10]采用斗鸡博弈来进行单交叉口交通控制,但未考虑交通信号设置。于是,一些学者结合合作和非合作博弈进行信号控制交叉口相位协调控制研究。彭敏等[11]采用二人合作博弈确定交叉口放行方向以及二人非合作博弈来确定该方向上各信号灯放行时间来建立交叉口交通信号博弈模型。Zhao等[12]提出了基于协调博弈和Pareto效率的交叉口交通信号控制,利用非合作博弈框架对交叉口进行建模,利用合作博弈模型中的Pareto效率概念进行求解。也有学者利用联盟博弈研究单交叉口交通信号控制。如卢维科等[13]建立了以执行绿灯的相位和下一相位为联盟的单信号交叉口合作博弈控制模型。但是上述研究对相位合作时交叉口交通信号控制系统的渐近稳定性缺乏深入的研究。
也有学者将车联网和博弈论相结合研究交叉口交通信号控制。Xu等[14]提出了一种V2I技术环境下延误车辆选择路径与交通信号调整之间的博弈模型,但参与人不是相位。谈判博弈作为一种合作博弈,将其应用于交叉口各相位协调控制的研究较少。Tan等[15],Abdelghaffar等[16]利用纳什谈判解来优化交叉口交通信号控制,但缺乏算法的稳定性分析。Valencia等[17]、夏新海等[18]尝试利用谈判博弈进行多个交叉口交通信号协调控制,但缺乏信号控制交叉口效用空间的凸性分析,因此在交通需求处于过饱和状态时不一定能保证算法的最优性。
谈判博弈模型允许各参与者之间通过交互信息进行协商,适合离散动态交互问题建模。鉴于此,本研究主要目的是利用谈判模型建立信号控制交叉口相位间博弈协调框架,将其转化为局部数学规划问题,并对其相位效用空间进行了凸性分析。在此基础上,设计有效的求解算法,并对算法的稳定性进行理论分析。最后设计不同的交通需求情景,验证所提出算法的有效性和稳定性。
因此,本研究就理论贡献而言,对相位效用空间的凸性和相位合作时交叉口交通信号控制系统的稳定性进行了理论分析。从方法论的角度来看,相位利用感知的效用选择合作,保持相位局部控制决策的有效性,并尽可能实现整个交叉口信号控制的效率,以计算效率高的方式找到相位信号控制问题的合作解决方案。
1 信号控制交叉口相位间谈判博弈模型
本谈判博弈模型针对信号控制十字交叉口。以其信号控制交叉口两相邻相位为例,相位1和2(其中相位1为某一时刻末将要执行绿灯相位,相位2为相位1的下一相位)总是存在一种矛盾。随着绿灯时间的增大,执行绿灯相位1的平均车辆排队长度变小,而执行红灯相位2的平均车辆排队长度在增加。这种交互可以描述成两个相位对绿灯资源的博弈。
因此,城市交叉口交通信号控制中每个相位在进行局部交通信号控制时均受到其他相位局部交通信号控制的影响,并且每一相位需要在交叉口交通信号控制性能和相位局部交通信号控制性能之间进行权衡,使得各相位间交通信号控制能够共创双赢,因此各相位间为了相互的利益需要进行合作,进行控制动作等信息的交互。此交互环境属于离散动态交互。车联网技术的发展使得各相位之间以及各相位和交叉口交通信号控制器之间能交换性能指标和控制方案等信息,因此交叉口交通信号控制问题可用时间离散动态谈判博弈框架来描述。
假设交通信号控制交叉口由M个信号控制相位组成,其信号周期为C(s),最大和最小周期分别为Cmax,Cmin,相位的绿灯间隔时间为Ii(s),每个相位的绿灯持续时间为Gi(s),相位最小绿灯时间为Gmin(s)。
定义此谈判博弈模型为元组G=(N,{Ai}i∈N,{φi(a(k)}i∈N,{ηi}i∈N)。其中N={1,…,M}为信号控制交叉口中各相位的集合。
Ai为信号控制交叉口中第i个相位的可行动作集合。对于每个相位,其动作ai∈Ai,Ai={1,0}。其中,动作1表示保持绿灯指示,意味着没有信号变化(即绿灯指示将保持绿色;红灯指示将保持红色)。动作0表示改变绿灯指示,意味着交通信号指示将在仿真时间间隔内改变(即绿灯指示将变为黄色,然后变为红色;红灯指示将变为绿色)。当某一个相位保持绿灯指示,而所有其他相位保持红灯指示。
φi(a(k)):A1×…×AM→R:为在时间步k时,当信号控制交叉口各相位采用联合动作a(k)时第i个相位的效用函数,其决定了信号控制交叉口中第i个相位的喜好和策略,并给出了一定程度的理性。其中a(k)为联合动作向量,a(k)=(a1,a2,…,aM)。
博弈中每个相位的效用函数φi可定义为应用特定动作后每个相位相应车道车辆排队长度总和的估计值,根据如下思路计算。
在仿真中,使用Vissim软件监控车速,假设车辆与交叉口交通信号控制器有某种形式的通信(即,车辆与基础设施[V2I]通信),或使用闭路电视摄像机的视频图像处理器的检测能力,包括车辆排队检测、车辆方向的检测、车速检测,并且计算出进入交叉口的车流。所有进入车道的这些参数都会不断更新。
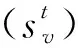
(1)
(2)
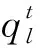
每个相位的效用为:
(3)
式中,Δt为更新时间间隔;Qi(t+Δt)为相位i在Δt之后的估计排队长度;Qinl为车流到达率(veh/h/车道);Qoutl为车流驶出率(veh/h/车道)。Qoutl通常在连接的下游端测量,而Qinl则在距离连接的下游端相当于阻塞密度上的谈判初始点值(定义见下文)处测量。
使用运动学公式(4)来估计Qinl,其中sgn(x)是符号函数。
(4)
对于Qoutl,计算可分为3种情况。对处于绿灯相位并希望保持当前相位(条件c1)的相位,可以简单地使用饱和流率进行估算;对处于红灯相位并希望切换到绿灯相位(条件c2)的相位,不能使用饱和流率(绿灯相位将刚刚开始),因此使用运动学公式来估计;对于其他条件,驶离车辆的数量为零。因此Qoutl的公式如(5)所示:
(5)
式中,μl为车道l的饱和流率;ΔL可用如下公式估算:
(6)

ηi为信号控制交叉口中第i个相位的谈判初始点,为期望性能的最大损失,其反映信号控制交叉口中第i个相位是否参与合作的意愿。
交叉口交通信号控制的目标是使不同相位的排队长度最小化并相等。根据文献Nash[19]的双人博弈谈判模型,此博弈问题可转化为如下局部线性数学规划问题(其中log(_)函数来自于Nash乘积的转换)来求解最优动作:
(7)
s.t.:
ηi(k)≥φi(a(k));Cmin≤C≤Cmax;
式中wi=1/M。
2 信号相位效用空间凸性分析
根据文献Nash[19],若效用空间{φi(a(k)}i∈N为有界的闭凸集,则式(7)存在唯一的最优解,即能保证收敛到最优解。因此,为了设计有效算法求解谈判博弈模型,需要对信号控制相位效用空间凸性进行分析。
设一信号周期长为C的交通信号,其有效红灯时间为R;有效绿灯时间为G;有效绿灯时间内的饱和流率为μ;车辆平均到达率为λ;通行能力为c(c=μG/C);一个周期内的服务车辆数为n′(n′=λC);延误车辆数为n。
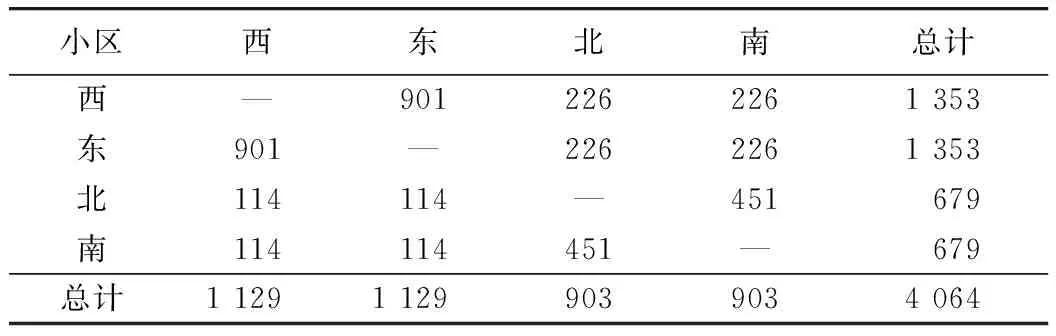
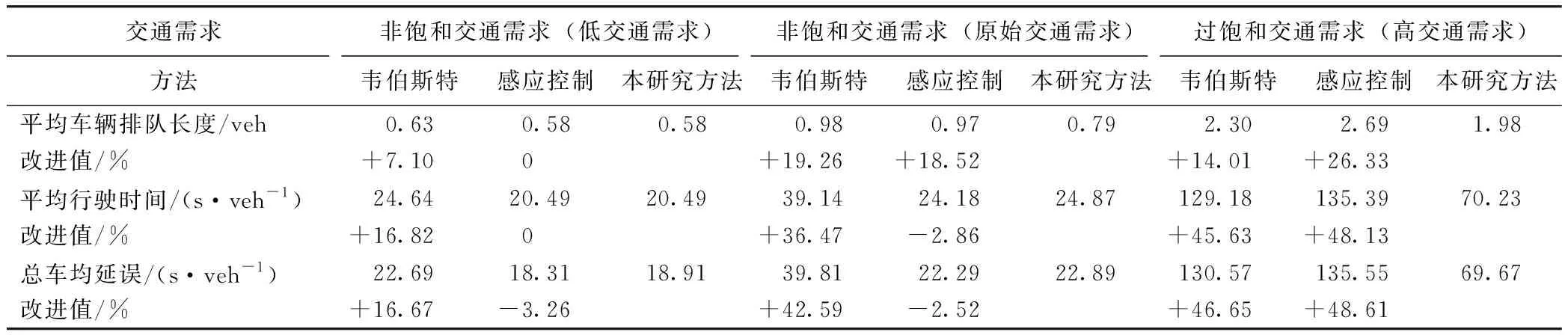
(1)非饱和交通需求下(λ 非饱和交通条件下一个信号周期内全部车辆的总延误时间,用ω(veh·s)表示,可以得到一个周期内每辆车的平均延误时间为[20]: (8) 设G1,G2为两个相位(南北车流和东西车流各一个相位)的有效绿灯时间;L为损失时间;μ为进口车道饱和流率;λ为进口车道到达率,则有R1=L+G2,R2=L+G1,并且L=C-G1-G2。 4个入口车道的总车均延误为: (9) 式中i为入口车道编号。根据式(8)、(9)有: (10) 将R1,R2,C用L,G1,G2替换,4个进口道上的平均车辆排队长度之和为: (11) 因此,需要证明车辆排队长度函数(y)是一个凸函数。令 式中,a,b,c,d是正常数,于是有: (12) 设η为特定车道上可存储的最大车辆排队长度,根据前述,博弈效用定义为车辆排队长度,即φ=y。因为完成了这一步的y是一个凸函数,所以不等式(y(G1,G2)≤常数)定义了一个凸集,即φ≤η为凸集。式(12)可以推广到任意数量有多个流向车流的相位。 因此对于非饱和交通需求,效用空间是凸的,局部优化问题(7)能保证收敛到唯一的最优解。 (2)过饱和交通需求(λ>c),效用空间不是凸的 对于过饱和的交通条件,绿灯间隔(即λiC>μiG)结束时,排队车辆没有被清除,剩余的排队车辆在整个分析时间段T内持续增加。 为了计算在绿灯期间无法提供放行服务的排队车辆数,必须在式(12)中添加4个进口道与过饱和延误有关的附加项(y2)。过饱和平均排队长度(y2)为: (13) 式中,Zi为正增凸函数;Z-1为正减凸函数;μi为正常数。因此,μi(Zi-L)Z-1为一个凸函数,-μi(Zi-L)Z-1为一个凹函数。于是,对于过饱和交通需求,总排队长度函数不是凸函数。 因此,对于过饱和交通需求,效用空间不是凸的,当车辆排队溢出超过初始参考点时,局部优化问题(6)不能保证收敛到最优解。 (1)保证算法的最优性 根据本研究第2部分研究结论,对于非饱和交通需求下,局部优化问题(6)是可行的,算法能保证收敛到唯一的最优解。而对于过饱和交通需求,局部优化问题(6)不可行。因此,为了保证算法收敛到最优解,算法在当时间步k=0时,将相位谈判初始点设置为基于车道长度可容纳的最大可测排队长度。 (2)避免繁琐的迭代过程 算法由一系列步骤组成,其结果是以合作或非合作的方式解决局部优化问题(6)[19]。信号控制交叉口相位i与其他相位j交换动作、谈判初始值,可以避免繁琐的迭代过程,信号控制交叉口各相位根据从合作行为中感知的效用来决定是否合作。 (3)合理构建初始点 给定谈判初始点的更新条件,其值降低(这意味着相位i决定合作)为增加合作行为的需求提供了强有力的激励;但是,使其值等于效用函数的当前值(意味着相位i决定不合作)为改变不合作的决策而提供了激励。鉴于此,ηi值构建如下: (14) 式中α为系数,0≤α≤1。 (1)时间步k=0,每一相位的ηi设置为相位所属的基于车道长度可容纳的最大可测车辆排队长度。 (2)在每一时间步k,每一相位i将ai,ηi值发送给其他相位。 (3)对于每一相位i=1,…,M,根据接收到的其他相位的信息,求解局部优化问题(7)。 (5)每一相位更新其谈判初始点。如果局部优化问题(7)可行(非饱和交通需求下),相位i根据ηi(k+1)=ηi(k)-α(ηi(k)-φia(k))来更新谈判初始点。如果局部优化问题(7)不可行(过饱和交通需求下),相位i根据ηi(k+1)=φia(k))更新谈判初始点。 (6)所有相位将更新的控制动作和谈判初始点发送给其他相位。 (7)转到步骤(2)。 从算法流程中看出,该算法只需求解一个优化问题,其减少了有关相位之间的通信,减轻了在每个时间步处理多个优化问题的有关分布式交通信号控制的计算负担。 谈判博弈模型求解算法的稳定性取决于每个相位是否决定合作。因此,为了证明此方法的稳定性,考虑了两种情况: (1)所有相位总是相互合作。 (2)一些相位不合作,仅在少量的时间步内开始合作。这里不考虑所有相位决定不合作的情况,因为根据第3.1节中提出的谈判初始点的构建,这种情况只有当k→∞,φi(a(k))→∞发生。根据前述,对于不合作的相位有ηi(k+1)=φi(a(k))。 (15) (16) (17) (18) (19) 在时间步k+1, 全局效用函数的初始值由式(20)给出: (20) 根据式(16)有: (21) 并且根据式(19)有: (22) 其中有 a-i(k)], (23) (24) 式中M(k)≤0,定义如下: (25) (1)∀(a(k))≠0,L(a(k))≠0, (2)对于a(k)=0,L(a(k))=0, (3) ∀k,L(a(k+1))-L(a(k))≤M(k)。 其中M(k)为k的一个非递增函数时,控制系统的状态收敛到原点附近。因此,系统是稳定的。由于不能证明M(k)收敛到原点,因此在一般情况下不能保证渐近稳定性。 一种特例是所有相位总是决定合作,即∀k,C(k)=N。在这种情况下: (26) (27) (28) 因此: (29) 那么有 (30) 根据前述,L(a(k))为二次正凸函数,满足: (1)∀(a(k))≠0,L(a(k))≠0。 (2)对于a(k)=0,L(a(k))=0。 所以有: (1)∀k,Mc(k)>0。 (2)L(a(k+1))-L(a(k))是k的递减函数,其下限为0。 因此,L(a(k))满足Lyapunov函数的条件,并证明了当相位总是决定合作时交叉口交通信号控制系统的渐近稳定性。 仿真试验将在具有4个方向(东、南、西、北)进口道的十字交叉口进行测试,每个进口道由3条车道组成。划分4个相位,分别为:东西进口车流直行及右转,东西进口车流左转,南北进口车流直行及右转,南北进口车流左转。各相位原始交通需求(O-D)矩阵见表1,其在VISSIM仿真平台中设置。 表1 原始交通需求O-D矩阵(单位:veh/h)Tab.1 Original traffic demand O-D matrix(unit:veh/h) 采用韦伯斯特方法对固定配时方案进行优化,黄灯时间ty为3 s,全红时间为2 s。感应控制的最大绿灯时间和固定交通信号控制方案相同。感应控制的最小绿灯时间为6 s,最大绿灯时间为31 s,绿灯延长时间为2 s。因当Δt很小时,即接近黄灯时间时,对应切换函数的下一相位的效用函数在太短的有效绿灯时间内缓慢增加。当Δt较大时,由于使用的所有变量都是在一个时刻检测到的,因此使用的运动学公式见式(4)的估计将有较大的偏差,故取Δt=17 s。其他仿真参数值设置如下。 临界速度:sTh=3.6(km/h);饱和流率:μ=1 655(veh/h/ln);自由流速度:80(km/h);阻塞密度:150(veh/h/ln)。时间步k=0,各相位的谈判初始点设置为ηi=12。采用平均车辆排队长度、平均车辆行驶时间、总车均延误对本研究方法、韦伯斯特固定信号控制和感应控制方法的性能进行评价。 以韦伯斯特的固定信号控制和感应控制方法为基准来评估本研究方法的性能。使用3个仿真场景:1个是表1所示的原始O-D交通需求矩阵;第2个是较低的交通需求,即原始O-D交通需求矩阵的80%;第3个是较高的需求,即原始O-D交通需求矩阵的120%。第1和第2个交通需求属于非饱和交通需求,第3个交通需求属于过饱和交通需求。 (1)算法有效性分析 表2给出了在原始交通需求下,Δt=17 s时,通过使用韦伯斯特的固定信号控制、感应控制方法和本研究方法得到的每条车道的平均车辆排队长度的均值和标准差。很明显,虽然本方法并不是对几乎所有车道都是最好的,但最后的结果表明本研究方法是最好的。另一方面,韦伯斯特方法在交通流量较大的相位效果较好,感应控制方法在交通流量较小的相位效果较好,这使得同一算法下不同相位的差异较大。然而,对于本研究算法,无论交通流水平如何,几乎所有车道的平均车辆排队长度都在同一水平上。由表2可知,采用本研究算法进行交通信号控制时,各个相位相关车道平均车辆排队长度波动趋势保持一致,即1个信号周期结束时,不同相位之间平均车辆排队相差不大,较好地实现了车辆排队长度均衡,表明了博弈中各个相位之间不是对立而是追求共同收益的关系。因此,可以将本研究算法具有更好的协调均衡性,以确保交通信号系统更有效。 表2 在原始交通需求下,不同方法下该测试交叉口各车道的平均车辆排队长度均值和标准差Tab.2 Standard deviations and mean values of average vehicle queue length for every lane of tested intersection by different methods under original traffic demand 不同方法和不同交通需求下本研究方法与韦伯斯特方法和感应控制方法相比性能改进情况见表3。可以看出,除了在较低的交通需求下感应控制方法运行较优外,本研究方法的3个有效性测试指标的平均值相比之下都取得更好的值。特别是过饱和交通需求(高交通需求)时,通过在时间步k=0时将相位谈判初始点设置为基于车道长度可容纳的最大可测排队长度,本算法仍然保证收敛到最优值,并且相对于非饱和交通需求,改进效果更好。 表3 不同交通需求和不同方法的性能指标值Tab.3 Performance indictors obtained by different methods under different traffic demands (2)算法稳定性分析 表4显示了不同交通需求下不同性能指标的标准差,可以看出本研究方法除了在较低及原始的交通需求下部分指标的标准差略低于感应控制方法的部分指标的标准差外,其他情况标准差明显低于另外两种方法,即各相位车流到达率类似的情况下,平均车辆排队长度等指标不会出现较大波动。这是因为相位在决定合作过程中进行动作和谈判初始点的交互,交叉口交通信号控制系统具有一定的渐近稳定性。因此本研究方法更稳定。 表4 不同交通需求下不同方法的性能指标值的标准差Tab.4 Standard deviations of performance indictors obtained by different methods under different traffic demands 本研究提出了一种基于实时谈判博弈优化模型的信号控制交叉口相位协调控制方法。在进行相位效用空间凸性分析的基础上设计有效的求解算法。此算法可以避免繁琐的迭代过程,并能保证算法在过饱和交通需求下收敛到最优解。对算法的稳定性进行了理论分析。当相位总是决定合作时交叉口交通信号控制系统具有渐近稳定性。通过仿真试验分析对该算法与韦伯斯特方法和感应控制方法在平均车辆排队长度、车均行驶时间和平均总延误方面进行了比较。结果表明,在不同交通需求下,该方法具有更好的有效性和稳定性。 未来进一步将本研究的算法扩展到多交叉口,并引入智能网联技术[22],以利于城市交通信号协调控制。另外,本研究采用可变相序,虽然可以通过提取道路数据选取最有价值通行相位,但是改变交叉口的相序时没有考虑驾驶员停车按相位顺序等待绿灯的习惯,以及由于相位切换造成的处理冲突的时间变长问题,这些将是以后的研究方向。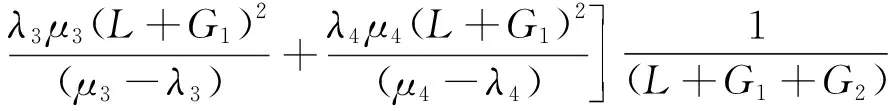
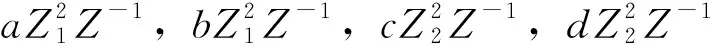
3 谈判博弈模型求解算法设计
3.1 基本思想
3.2 算法流程
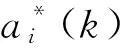
4 算法稳定性理论分析
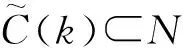
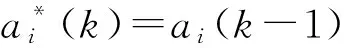
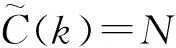

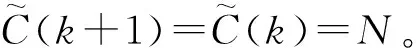
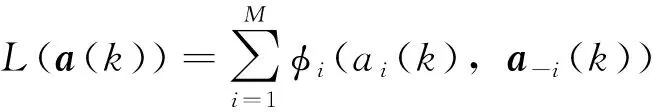
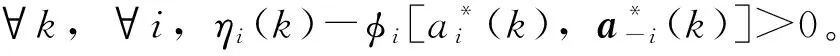
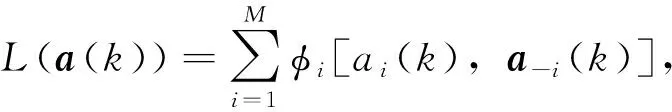
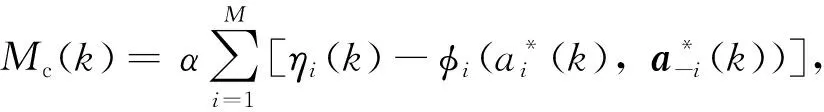
5 仿真试验分析
5.1 测试交叉口
5.2 仿真参数和测试指标
5.3 结果和讨论


6 结论

