具多时滞及多重非线性Lurie间接控制系统的绝对稳定性

王 宁,周宗福

(安徽大学 数学科学学院,合肥 230601)

20世纪40年代，Lurie和Postnikov首次提出了控制系统的绝对稳定性问题。[1]从此，人们对Lurie系统的绝对稳定性问题进行了很多研究并得到了大量成果。[2-8]在这些成果中，研究的系统主要有常微Lurie控制系统及时滞Lurie控制系统，其研究方法包括构造Lyapunov函数、M-矩阵的性质、线性矩阵不等式等。文[9]利用李雅普诺夫方法给出了多时滞Lurie控制系统的稳定性条件。最近，文[10]对单个变时滞Lurie间接控制系统的绝对稳定性进行了研究，获得了简便实用的绝对稳定判定结果。在此基础之上，本文研究了具有多个变时滞的多重非线性Lurie间接控制系统的绝对稳定性问题，给出绝对稳定的充分条件，扩展了已有的结果。

1 系统描述

考虑如下具有多个时变时滞的多重非线性Lurie间接控制系统：

(1)

对于系统(1)，假定下列条件成立：

(I1)x(t)∈Rn；σl(t)∈R(l=1,2,…,m)；A(t)，Bi(t)(i=1,2,…,q)为n×n矩阵；bl(t)，cl(t)(l=1,2,…,m)为n维列向量；

(I3)A(t)，Bi(t)，bl(t)，cl(t)，ρl(t)在(0,+∞)上连续；fj:(-∞,+∞)→(-∞,+∞)；φ(t)为初始函数。

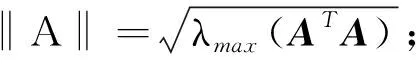
定义1设F[kl1,kl2]={fl|fl(0)=0;kl1σ2l(t)≤σl(t)fl(σl(t))≤kl2σ2l(t),σl(t)∈R-{0},kl2>kl1>0}，若对∀fl∈F[kl1,kl2](l=1,2,…,m)，系统(1)的零解都是全局渐近稳定的，则称系统(1)是绝对稳定的。

2 主要结果

基于Lyapunov方法，通过构造合适的Lyapunov-Krasovskii泛函，并分析其全导数的负定性，本文给出了系统(1)绝对稳定的判据。

定理1对于系统(1)，假设：

(H1)存在正定矩阵P，Gi(i=1,2,…,q)，Rr(r=1,2,…,m)，使得

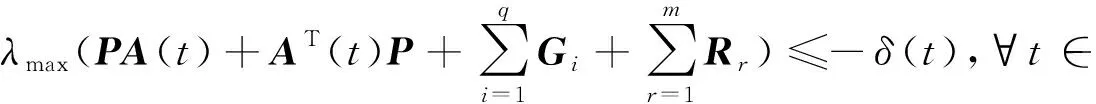
其中δ(t)≥δ0>0；

(H2)∀t∈[0,+∞)，有

其中ηi，ζj，γl为正常数，令γ=max{γ1,γ2,…,γm}；

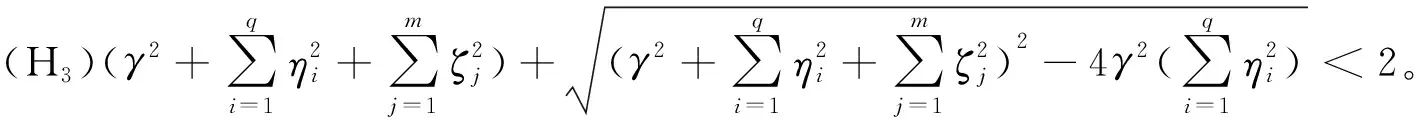
证明作Lyapunov-Krasovskii泛函

V(t,φt)=

其中φt(θ)=(x(t+θ),σ1(t+α1(t)),…,σm(t+αm(t)))T，θ∈[-h,0]，t≥0。

∀fl∈F[kl1,kl2]，易知

因此

进而，有

令

则

u(‖φt(0)‖)≤V(t,φt)≤v1(‖φt(0)‖)+v2(‖φ‖L2)。

下求V(t,φt)沿系统(1)的导数：

利用(H1)、(H2)及范数性质，上式变为：

上式右端可写成如下形式:

(2)

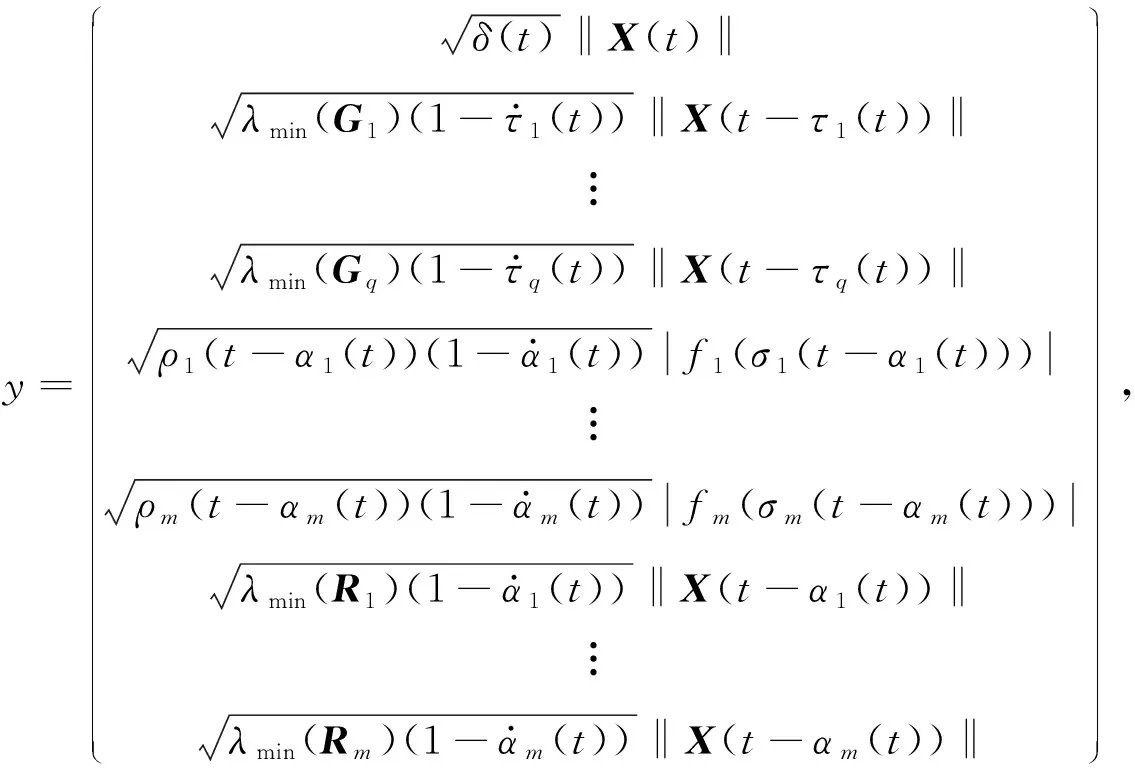
下证(2)式右端是负定的。易知D的特征多项式为

可见D的特征值为：

λ1=-1(q-1重)，λ2=-1+γ(m-1重)，λ3=-1-γ(m-1重)

易见，D的最大特征值为λ4.由(H3)知，λ4<0，从而D的每个特征值都小于0，故D为负定矩阵.

结 合(2)式，有

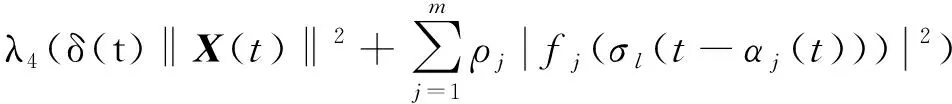
kl1σ2l(t-αl(t))≤σl(t-αl(t))fl(σl(t-αl(t)))

所以

kl1|σl(t-αl(t))|≤|fl(σl(t-αl(t)))| (l=1,2,…,m)

因此

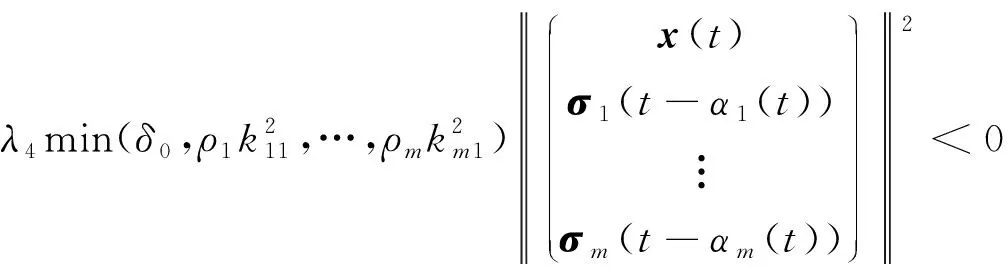
则对所有的fl∈F[kl1,kl2],l=1,2,…,m,有

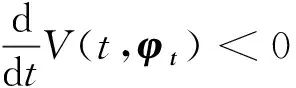
根据定义1和Lyapunov定理可知，系统(1)是绝对稳定的。

注文[10]是对单个变时滞Lurie间接控制系统的绝对稳定性进行了研究，而本文讨论的是具有多个变时滞的多重非线性Lurie间接控制系统的绝对稳定性问题，问题更加一般化，所得结论适用性更广。