盾构隧道设计轴线偏移解析算法研究

李永明，李长俊，郑国平，陈秀平

（1. 浙江数智交院科技股份有限公司，浙江杭州 310030； 2. 浙江工业大学土木工程学院，浙江杭州 310014；3. 绍兴市柯桥区交通投资建设集团有限公司，浙江绍兴 312081）

1 引言

近年来，盾构工法作为我国大型越江海隧道和城市地铁建设不可或缺的关键技术[1]已经取得了举世瞩目的成绩[2-3]，目前正朝着基于韧性理念的智能化建造方向开拓发展[4-5]。但正如陈湘生院士指出：目前隧道管片拼装大量依靠人工，误差大[4]，不利于建设韧性的隧道。要提高隧道的拼装质量，掌握盾构隧道设计轴线（Designed Tunnel Axis， DTA）是基础，DTA是由平面曲线和纵面曲线构成的空间复合曲线。盾构工法施工通过衬砌管片组合拼装来拟合DTA；而盾构隧道轴线控制不好，往往导致管片成型质量差，甚至破损严重，给隧道服役寿命的缩短埋下隐患。我国从2004年开始使用的通用楔形环管片近年来已逐渐成为主流管片形式；但通用楔形环管片相对于传统的直线环+左右转弯环管片，对拼装施工要求更高，操作难度更大。

为提高盾构隧道管片拼装的质量，国内学者针对DTA上任意点的空间坐标解析及通用楔形环排版算法做了很多研究工作，如郑国平等[6-8]研究了平纵曲线上任意点的定点坐标算法；钟宏斌等[9]、金蕾等[10]编制了路线坐标计算程序；吴海彬等[11]研究了管片结构尺寸参数、初始轴线偏差与最小拟合半径之间的关系；董秀竹等[12]提出了衬砌环平面和高程偏差的计算方法；阮承志[13]研究了平面圆曲线段和缓和曲线段管片排版原则；冯天炜等[14]提出了一种四维坐标（x，y，z，φ）用于管片结构空间定位方法；一旦实际隧道轴线出现偏差，则需要基于相应的纠偏算法进行及时的纠偏，王运钢[15]、杨建伟[16]等对此开展过相关研究。

然而，既有的研究都忽视了一个实际问题，即在实际工程中经常碰到设计轴线（平、纵曲线）与结构中心线或者导航基准线不重合的情况；比如，地铁隧道的设计线通常位于轨面中点，公路隧道的设计线一般设在路缘，与隧道结构中心线在水平和垂直方向都有一定的偏差。于是，当曲线长度较长时，将通用楔形环按设计平曲线排版就容易出现若干环的误差。因此，为提高拼装的精度，有必要将设计轴线通过一定算法偏移至导航基准线结构中心。而对于平、纵曲线偏移的算法，现有文献、规范中均尚未有述及。施工单位多采用图上逐点手工平移的方法；当路线半径较小、区间隧道较长时，该方法会引起较大的误差。因此，本文拟采用解析方法提出盾构隧道设计轴线偏移解析算法以解决相应难题。

2 平面曲线偏移算法

2.1 平面曲线的参数

公路、地铁等交通隧道的平面线形通常由直线、圆曲线、缓和曲线构成；其中，缓和曲线设置在直线与圆曲线、圆曲线与圆曲线之间，使整条曲线的曲率连续变化且相应变化过程更加平缓。缓和曲线的平曲线各特征点的技术代号如下：

（1）JD表示“交点”（转角点）；

（2）ZH表示“直缓”（第一缓和曲线起点）；

（3）HY表示“缓圆”（第一缓和曲线终点）；

（4）QZ表示“曲中”（曲线中点）；

（5）YH表示“圆缓”（第二缓和曲线起点）；

（6）HZ表示“缓直”（第二缓和曲线终点）。

平曲线各个几何要素，包括切线长、曲线长、圆曲线长、外矢距、校正值等数值的计算方法可参考道路勘测设计的相关书籍。

2.2 偏移算法解析

图1为平曲线偏移算法示意图，对照图片所示，原平面曲线为红色，偏移后的新平面曲线为绿色，HY点到YH点之间为圆曲线，ZH点到HY点以及YH点到HZ点为缓和曲线，缓和曲线两端为直线。首先，将原平面曲线两端的直线偏移ΔR后得到新平面曲线的直线，根据新的直线方程不难求得新交点JDn的坐标；并进而求得新交点与圆心O的距离和新的圆曲线半径Rn（Rn=R+ ΔR），两者之差即为新的外距值En。因为偏移不会改变平曲线的偏角α，所以，可以由外距公式（1）求得新平曲线的内移值Pn，由内移值公式（2）求出新平曲线的缓和曲线长度Lsn，由公式（3）求得新的曲线角β0n，由公式（4）求得新的切线增值qn，由公式（5）求得新的切线长Tsn，最后由公式（6）求得曲线长Ln。至此已完成了对新平曲线的各特征参数的求解。根据偏移后的新交点坐标，重新计算各新交点之间的平面距离，可以得到各个新交点的里程桩号，并进而获得各个特征点（ZH、HY、YH、HZ）的里程桩号。

3 纵面曲线偏移算法

3.1 纵面曲线的参数

在纵断面上两个坡段的转折处，为便于行车，会设置一段曲线用于缓和坡度，该曲线被称为纵面曲线或竖曲线。变坡点BP是相邻两条坡度线的交点，变坡角是相邻两条坡度线的坡角差，通常用坡度值之差来代替。根据前后坡度的大小和坡向，竖曲线又分为凹型竖曲线和凸型竖曲线。

3.2 偏移算法解析

对纵面曲线的计算则采用投影法，将变坡点BP从DTA投影到导航基准轴线上，即可以得到新的变坡点里程桩号（图2）。当初步判断投影变坡点BP’位于直线段上式，已知偏移后得到的导航基准线直线方程为ax+by+c= 0、BP点在DTA上的坐标值（m，n），则投影变坡点BP’也即垂足点的坐标（x，y）可以由公式 （7）算得，然后通过比较BP’点的x或y坐标数值是否位于直线两个端点的x或y坐标之间，即可以判断此点是否真正位于直线的两个端点之间；如果不是，则需要进一步搜索附近的缓和曲线和圆曲线。

当初步投影变坡点BP’在缓和曲线上时，由于缓和曲线通常采用若干折线组成的多段线来近似表示，可以逐段搜索各条折线，然后用上述任意点到直线的垂足点坐标计算方法来求得；同样地，需要判断求得的垂足点是否真正位于该段折线上。

当初步投影变坡点BP’在圆曲线上时，则通过BP点与圆心O的连线方程，以及偏移距离ΔR，可以求得BP’的坐标。设圆心O的坐标为（xO，yO），BP点的坐标为（xBP，yBP），则BP’点的坐标可以由公式（8）算得。

4 算例

表1为某盾构隧道DTA平曲线参数，实际导航系统的基准线与DTA平面偏移距离为5 m，根据本文提出的算法，其导航基准线平曲线参数计算结果如表2所示。表中，X（N）、Y（E）分别表示经度和纬度方向的坐标，Ls1、Ls2分别表示两端缓和曲线的长度，T1、T2分别表示两端切线的长度。

表1 DTA平曲线参数 m

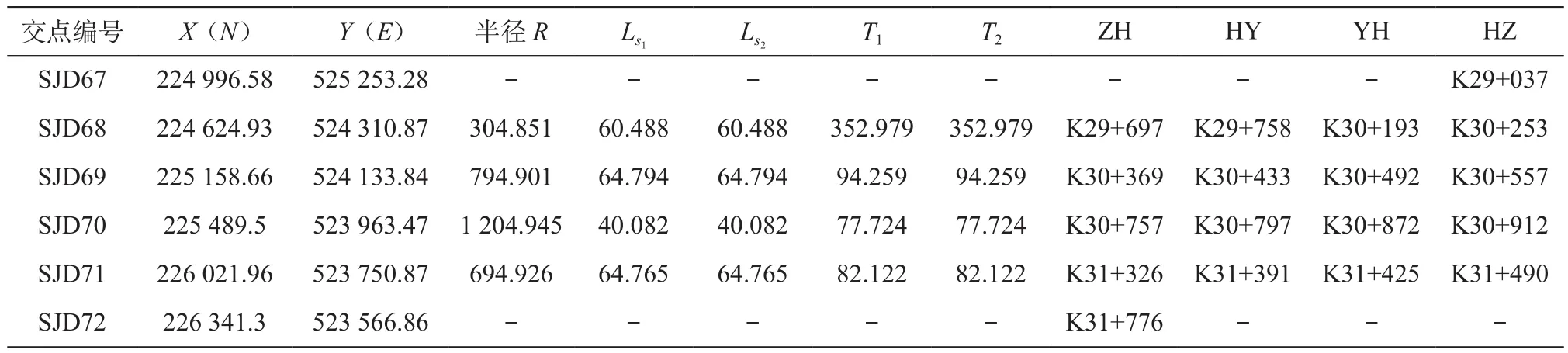
表2 导航基准线平曲线参数 m

表3为该盾构隧道DTA和导航基准线纵面曲线的参数。可见，实际导航基准点比DTA基准点高2 m，通过投影算法得到了新的变坡点里程；而其余数则保持不变。

表3 DTA和导航基准线纵面曲线参数

5 结语

本文采用平纵曲线偏移解析算法，实现了设计轴线到结构中心线或任意导航基准线的偏移，为拼装模拟提供了更加精准的基准。同时，此算法可采用于道路定点、放样等，以获得精确的定位。