基于脉冲频率与输入电流关系的SNN训练算法

兰浩鑫，陈云华

广东工业大学 计算机学院，广州 510006

脉冲神经网络（spiking neural network，SNN）通过脉冲事件驱动的通信实现神经元和突触计算，其与事件传感器相结合，有望突破深度人工神经网络所面临的能源和吞吐量瓶颈，实现低功耗、低延迟和高精度的目标识别[1]。然而，由于SNN采用的是生物神经元模型，使得SNN同时具有空间和时间特性，生物神经元相较于人工神经元有着复杂的时间动力学和离散脉冲事件产生过程不可微的性质，导致反向传播（backpropagation，BP）算法难以直接应用于SNN训练。

为此，研究者提出线性假设、忽略不可微、替代微分函数等[2-8]方式，使得可利用BP算法对SNN进行训练。现有研究主要分为基于时间编码和基于频率编码两大类。

基于时间编码的方法主要包括线性假设法和因果集法。Bohte等人[2]提出的SpikeProp及Ghosh-Dastidar等人[3]提出的Multi-SpikeProp都是基于线性假设，将神经元的输入时间和输出时间进行线性处理，以绕过脉冲函数不连续的问题。Mostafa[4]基于网络前后两层神经元发放脉冲的时间关系，建立具有局部线性关系的因果集（causal set），求线性关系的梯度调整脉冲发放时间，使正确发放的神经元比其他神经元更早发放脉冲，通过因果集的关系来避免直接对脉冲函数求梯度。时间编码将信息编码到脉冲序列精准的时刻点，只需少量的脉冲就可以表达准确的信息，因此这类方法限制某些神经元或者全部神经元发放一个脉冲，发放的脉冲数较少，具有功耗低的优点，但由于网络结构只有一个到两个隐藏层的全连接结构，在较大型数据集上的精度不够理想。

基于频率编码的方法主要采用忽略不可微、近似脉冲函数、替换微分函数等方法解决神经元产生离散脉冲事件的不可微性。Lee等人[5]采用的是忽略不可微法，将膜电位作为可微信号来求梯度，对于膜电位的突变将其看作噪声而忽略，通过忽略不可微的方式来实现梯度的反向传播。Jin等人[6]采用的是脉冲函数近似法，将网络层与层之间的数据传递看作“宏观层面”，神经元内部的数据传递看作“微观层面”，将“宏观层面”和“微观层面”的数据传递联系起来，通过对脉冲时间函数的近似来求梯度。Wu等人[1，7-8]基于替换微分函数的方法进行反向传播，用矩形函数代替脉冲函数的微分函数，将膜电位带入矩形函数中得到梯度。这类方法通常具有卷积结构的SNN，因此在较大的数据集上精度较高，但由于频率编码将信息编码到脉冲频率，需要大量的脉冲来表达准确的信息，仿真时长较长，功耗较高。

上述算法，基于频率编码的方法比基于时间编码的方法识别精度高，但由于基于频率编码算法通常采用时间信用分配（temporal credit assignment）机制进行参数更新，导致学习效率较低。为此，本文针对SNN难以直接训练问题，对LIF（leaky integrate-and-fire）神经元脉冲频率与输入电流进行仿真实验，发现模拟脉冲序列与真实脉冲序列具有一致性，基于仿真结果建模得到脉冲频率与输入电流关系的显示表达，将其显示表达的导数作为梯度以解决神经元产生离散脉冲事件的不可微性，从而使得BP算法可以用于SNN的训练。针对采用时间信用分配机制的方法学习效率较低问题，本文通过LIF神经元响应机制进行参数更新来提高学习效率。本文在MNIST和CIFAR10数据集上进行精度测试，识别精度分别达到了99.53%和89.46%。在学习效率方面，本文方法在MNIST数据集上与同类型的SNN算法进行比较，实验结果表明本文方法的学习效率约为同类型算法的两倍。

1 模型及算法

1.1 LIF神经元脉冲频率与输入电流的显示关系

神经科学上LIF神经元模型的时间动力学方程及其响应机制可以描述为：

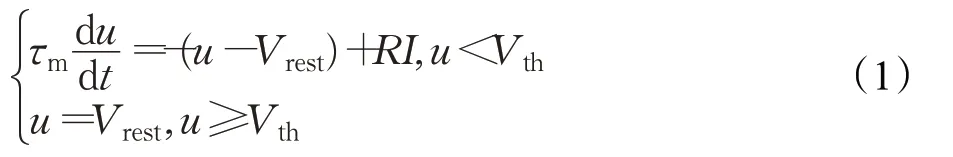
其中，τm代表时间常量；u代表神经元的膜电位；Vrest代表重置电位，本文置为0；I代表神经元接收到的输入电流，由前一层神经元的输出脉冲和突触权重决定；R为输入电阻。一旦膜电位u超过给定的阈值Vth时，神经元通过式（7）的脉冲函数发放一个脉冲，并且膜电位会回落到Vrest，式（7）的不可微性是导致BP算法不能用于SNN训练的主要原因。图1表达了上述描述的LIF神经元模型及其运行过程。

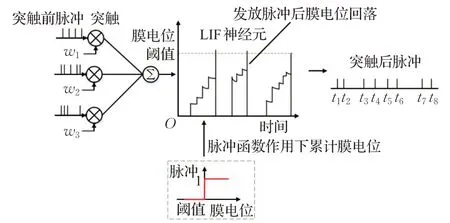
图1 LIF神经元模型及其内部状态变化Fig.1 LIF neuron model and its internal state changes

为了确定脉冲发放频率与输入电流的关系，生物学家将恒定的输入电流I注入到LIF神经元中，得到LIF神经元脉冲发放频率，可以表达为：

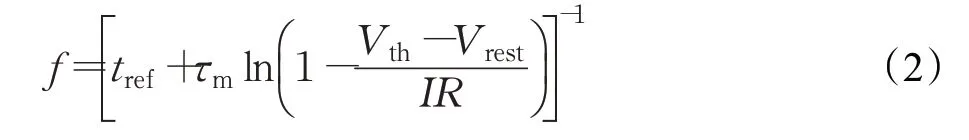
其中，f代表脉冲发放频率，tref代表不应期常量。

实践性、应用性较强的市场营销专业培养的毕业生应具有的创新、创业精神、创新创业能力，与创新创业教育的核心在本质上是一致的，将专业教育与双创教育进行融合是高等教育发展的改革路径之一。双创教育必须以专业教育为载体贯穿于人才培养的全过程，专业教育是双创活动的核心要素，二者相辅相成、相互融合、相互促进。专创融合教育的实践取向是构建综合型人才培养的高校教育体系，并通过构建综合型人才培养的教育目标、重构课程内容、加强学生创新技能培养的教学实践等予以实现。师资队伍在高校创新创业教育与专业教育互动融合中扮演着至关重要的作用，应当积极实施创新驱动，强化高校创新创业教育与专业教育互动融合中的师资队伍建设。

然而，真实的生物大脑接收到的是噪声电流，噪声产生的主要原因是大脑神经元离子通道开闭与神经递质的释放具有一定随机性。为此，神经学家通过实验建模的方式得到噪声电流下LIF神经元的发放脉冲频率表达式，即式（3）：

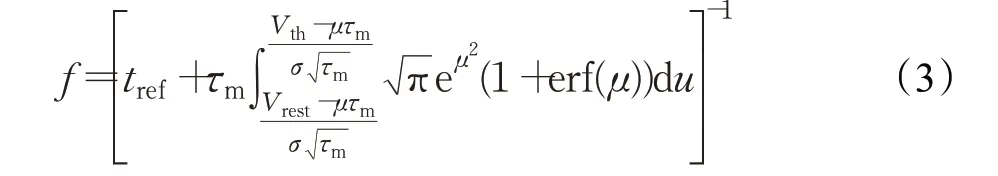
其中，μ、σ2代表输入噪声电流的均值和方差，erf(μ)为误差函数。

本文在实验仿真时需要采用基于频率编码生成的泊松脉冲序列（Poisson spikes train）[9]，因此需要确定软件仿真得到的输入电流和真实情况下带有噪声的输入电流LIF神经元的响应是否一致。通过在PyNN[10]平台上进行仿真，在噪声电流标准差为0.2、0.5、1.0的情况下，得到了不同噪声电流下仿真结果和真实情况下LIF神经元响应曲线，如图2所示[11]。

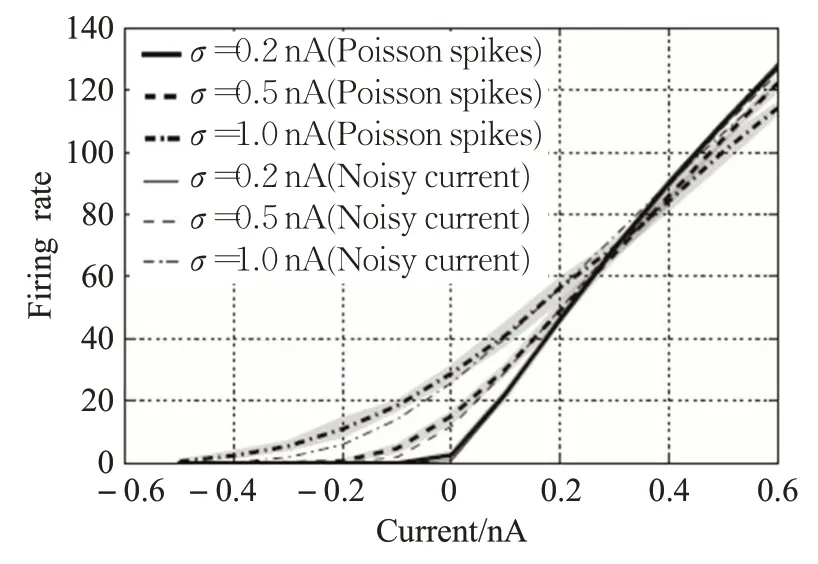
图2 泊松脉冲序列与真实LIF神经元的仿真结果Fig.2 Simulation result of Poisson spikes train and real LIF neuron

由仿真结果可知，采用泊松脉冲序列的LIF神经元响应曲线与真实情况下LIF神经元的响应曲线是一致的，因此采用泊松脉冲序列进行网络训练从生物学上讲是合理的。从理论上讲可以采用式（3）进行反向传播，但是式（3）是神经科学研究者通过实验建模所得，函数过于复杂，难以应用于实际的网络训练。此外神经科学领域研究发现，噪声电流通常是具有均值为0、标准差为1的高斯白噪声[12-13]，因此本文对图2中标准差为1的LIF神经元响应曲线进行建模，得到LIF神经元脉冲发放频率与输入电流关系的显示表达，如式（4）所示：

其中，α和β作为尺度因子，用于控制曲线的形状。

由于本文是基于上述LIF神经元脉冲频率与输入电流之间显示表达的导数作为反向传播的梯度，需要求得式（4）的导数，即式（5）：

1.2 训练算法

鉴于目前主流的学习框架（TensorFlow，Pytorch）要求神经元模型以离散序列的形式运行，但是式（1）在时间上是连续形式的LIF神经元模型，因此需要对LIF神经元离散化。目前出现了多种离散化LIF神经元的形式[7，14]，本文采用欧拉方程的解法来离散LIF神经元，得到如下在时间上离散的LIF模型：

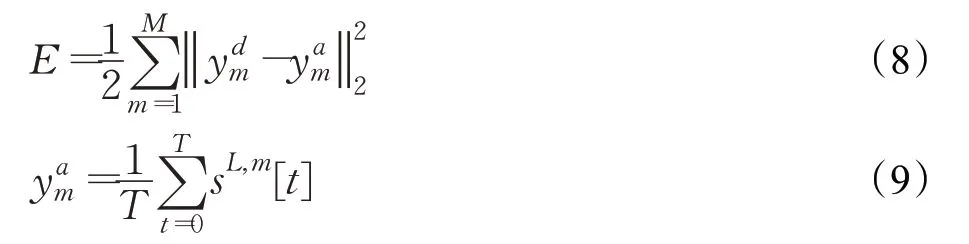
其中，M代表最后一层神经元的总个数，L代表脉冲神经网络的最后一层，T代表总时间步，分别代表输出层第m个神经元期望标签值与实际输出值，s L,m代表最后一层第m个神经元的输出脉冲。

本文是依据脉冲频率与输入电流的关系求得微分，因此定义网络中第l层第i个神经元脉冲的发放频率如式（10）所示：

第l+1层第j个神经元接收到第l层的脉冲而转换为总的输入电流，如式（11）所示：

（2）隐藏层

与输出层类似，仍需要计算误差函数E对权重w和初始膜电位b的微分，从而进行隐藏层的参数更新。首先结合式（5）定义误差项为：

至此，基于LIF神经元输出脉冲频率与输入电流关系的SNN训练算法的参数更新过程推导完毕。为便于说明，图3给出了本文采用LIF神经元响应机制与时间信用分配方法的参数更新对比图。从图3中可以看出，基于时间信用分配的方法需要在每个时刻进行前向和反向计算，这种计算方式学习效率较低，而本文方法在反向计算时根据LIF神经元响应机制只需更新一次参数，学习效率相较于基于时间信用分配的方法进一步提高。

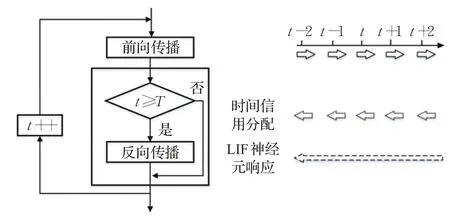
图3 时间信用分配与LIF神经元响应机制对比Fig.3 Comparison of time credit assignment and LIF neuron response mechanism

2 实验及相关结果分析

2.1 参数设置

本文方法的实验都基于Python3.7、Pytorch1.3进行软件仿真，硬件环境为CPU i5 10400，显卡GTX2060，内存16 GB的环境下进行实验。表1是本网络中使用的一些超参数设置，包括总时间步长、神经元阈值、LIF神经元的泄漏项、重置电位、控制脉冲频率与输入电流显示关系的尺度因子以及由Pytorch初始化的权重和膜电位，优化器采用的是Pytorch中Adam优化器。评估了本文方法在MNIST[15]和CIFAR10[16]两种分类任务上识别准确度，两种数据集的示例如图4所示，并将其与人工神经网络、将人工神经网络转换为脉冲神经网络的ANN2SNN算法、生物真实性较高的STDP（spike-timedependent plasticity）方法和直接训练SNN等方法进行比较。本文在学习效率方面测试了本文方法与采用时间信用分配机制SNN算法。

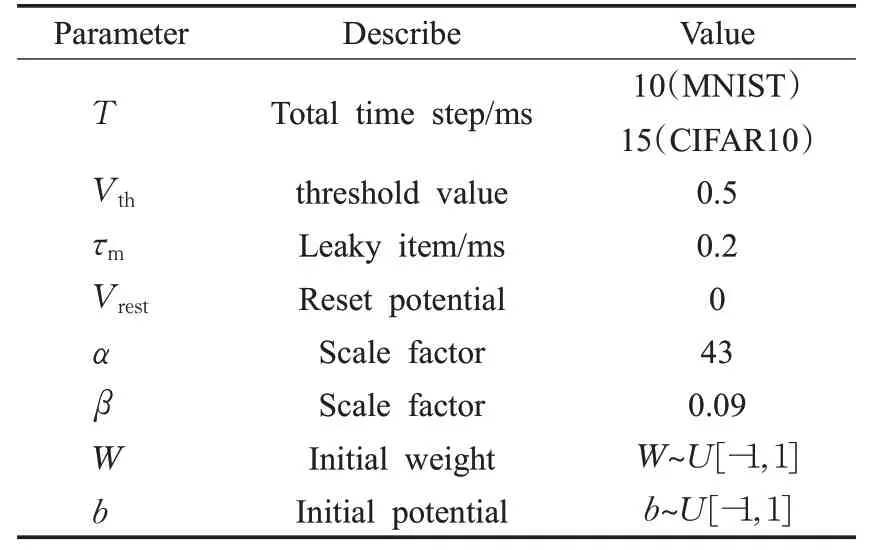
表1 网络中参数设置Table 1 Parameter setting in network

图4 MNIST、CIFAR10数据集Fig.4 Dataset of MNIST，CIFAR10

2.2 MNIST数据集测试

手写数字数据集MNIST是机器学习领域中最经典的数据集之一，其包括60 000张训练样本和10 000张测试样本，其示例如图4中顶部样本所示。由于SNN接收到的是脉冲数据事件，需要将静态图像转换为脉冲版本的事件流。对于静态图像，在频率编码领域，最常见的预处理是使用泊松编码将静态实值输入转换为脉冲输入，具体来讲就是对输入的特征向量在0到1范围内进行归一化处理，然后对每个特征维度生成泊松脉冲序列，该泊松脉冲序列的脉冲频率与归一化之后的特征值是成比例的。

表2是本文方法与同领域的其他方法精度比较，这些方法包括采用间接监督学习的ANN2SNN方法以及基于BP算法训练SNN的方法。表2中12C5表示有12个5×5的卷积核，P2表示平均池化核的大小为2×2，200FC表示有200个神经元的全连接层。本文网络所获得精度为10次实验数据集迭代100次的最好精度。由表2可知，本文方法达到了99.53%的精度，验证了本文方法的有效性，相较于Lee[5]的算法提高了0.22个百分点。

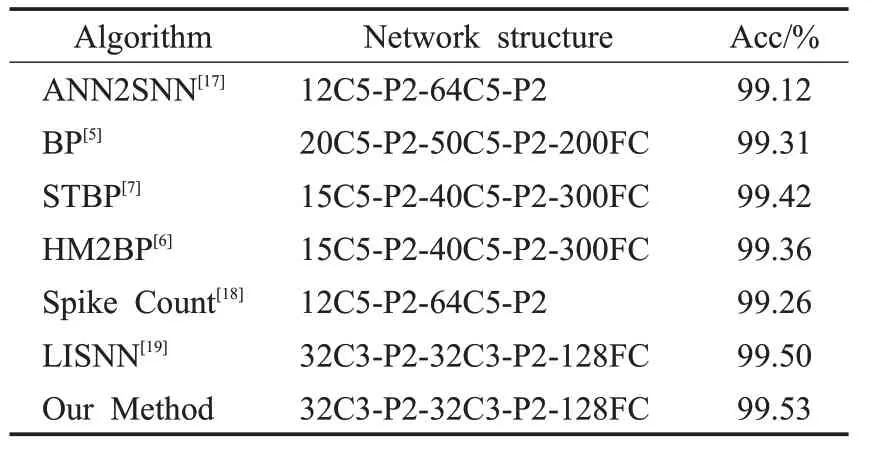
表2 MNIST数据集上的精度比较Table 2 Accuracy comparison on MNIST dataset

2.3 CIFAR10数据集测试

要证明算法的有效性，就应该在更大的数据集上进行测试。目前来看，CIFAR10相较于MNIST数据集对于SNN的训练有着更大的挑战，由于需要较多的时间步来表达精确的信息，具有训练成本较高难以收敛的问题，因此只有较少SNN版本的BP算法在此数据集上进行测试。CIFAR10数据集包括10个类别，50 000张训练样本和10 000张测试样本，其示例如图3中部区域所示。同样的，针对CIFAR10数据集本文采用如处理MNIST数据集相同的方法，通过泊松脉冲编码的方式将其转换为动态版本。

表3是本文算法在CIFAR10数据集上与ANN2SNN方法、具有高生物真实性的STDP算法和其他类型SNN版本的BP算法精度比较。图5是本文算法在CIFAR10数据集上随迭代次数变化的精度和损失曲线。通过表3可以看出，具有生物真实性的STDP算法因为只能部署在较浅的网络中，所以只达到了75.42%的识别精度。ANN2SNN是将人工神经网络训练完成的权重移植到SNN，这种方法虽然可以达到较好的精度，但是此方法需要额外的优化手段，如基于模型的归一化[20]、基于脉冲的归一化[21]等技术，并且此网络的延迟较大，通常需要上百个时间步来保证良好的性能。与ANN2SNN相比，采用BP算法训练SNN的延迟较小，通常在20个时间步以内。从表3中可以看出之前的STBP算法的精度已经达到了85.24%准确度，本文算法相对于此精度提高了4.22个百分点。

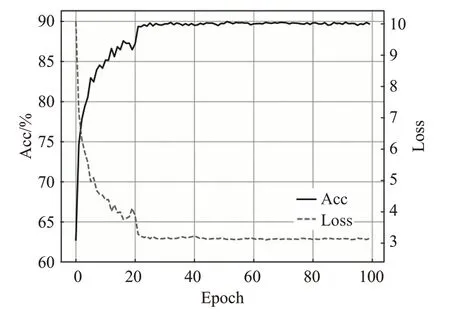
图5 CIFAR10数据集上精度和损失变化曲线Fig.5 Accuracy and loss change curve on CIFAR10 dataset

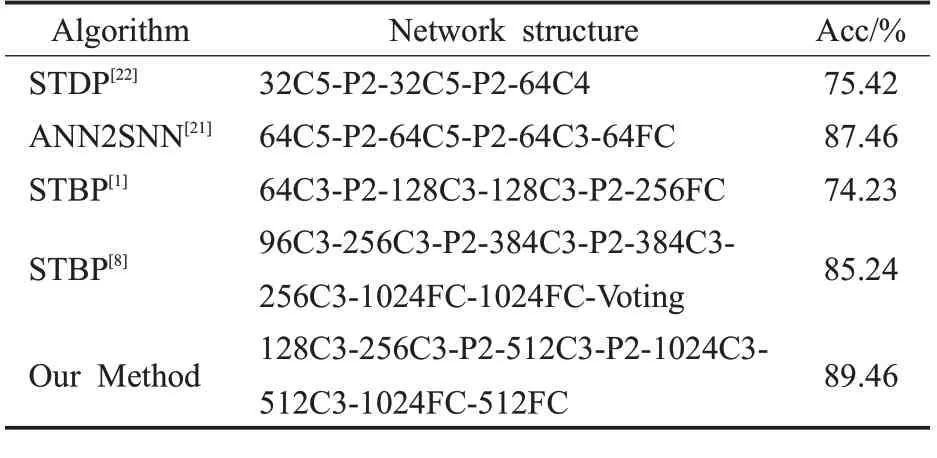
表3 CIFAR10数据集上的精度比较Table 3 Accuracy comparison on CIFAR10 dataset

2.4 学习效率比较

由于大部分SNN版本的BP算法没有在CIFAR10数据集上进行测试，本文选用常用的MNIST数据集进行测试。在相同网络结构下测试了本文方法与采用了时间信用分配机制的SNN版本BP算法，比较了在快速收敛到平稳收敛阶段所需的迭代次数与消耗时间，和训练完成后训练所需的迭代次数与消耗时间。

如表4所示，本文给出了测试所用网络结构、数据集大小、Batch大小、SNN的时间步个数T_step、迭代一次数据集所需时间One epoch，快速收敛到缓慢收敛时所需迭代次数C_Epoch与消耗时间C_Time，训练至网络稳定所需的迭代次数E_Epoch与消耗时间E_Time。图6是三种算法训练期间精度随迭代次数的变化。由表4可以看出，本文算法迭代一次数据集所需的时间大约为27.45 s，约为另外两种算法的一半。结合表4和图6可以看出，LISNN算法的快速收敛阶段为10个epoch，而本文算法和STBP算法大约为15个epoch。LISNN快速收敛所需epoch次数较短的原因是在LISNN网络中采用了独特的侧抑制机制优化算法，因此从迭代次数看可以更快收敛，但是所需的训练时间也会增加。由表4可以看出，在网络快速收敛阶段，本文算法比LISNN算法多了5个epoch，但是本文算法快速收敛所需时间411.8 s远远低于LISNN的709.3 s。另一方面，三种算法大约在100个epoch训练完成，本文算法训练完成后所需时间2 745 s也远远低于另外两种算法的6 294 s和7 093 s。从迭代一次数据集所消耗时间、快速收敛阶段所消耗时间以及网络训练完成时所消耗时间三方面都可以说明本文算法的学习效率高于采用时间信用分配机制的算法。

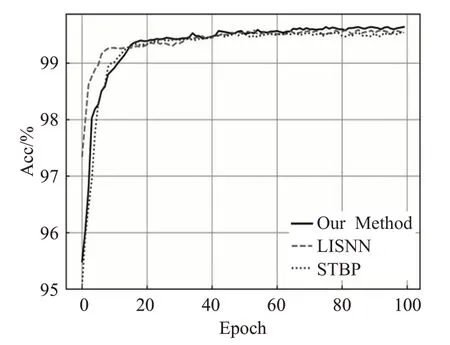
图6 三种算法精度随迭代次数的变化Fig.6 Accuracy change of three algorithms with number of iterations

表4 学习效率比较Table 4 Comparison of learning efficiency

3 结束语

针对脉冲神经元产生离散脉冲事件不可微而导致SNN难以训练问题，本文在研究LIF神经元响应机制的基础上，提出一种新的基于脉冲频率与输入电流关系的有监督式SNN训练算法。通过将每个LIF神经元脉冲频率与输入电流显示关系的导数作为梯度，解决了神经元产生脉冲活动不可微问题，使得可利用BP算法对SNN进行训练，在一些基准数据集上的识别精度取得了具有竞争性的结果。另一方面，针对现有方法采用时间信用分配机制进行参数更新导致学习效率较低的问题，本文采用LIF神经元响应机制进行参数更新，提高学习效率，实验表明本文算法是同类型SNN算法学习效率的两倍。