傅科摆运动规律的研究*
姜付锦 李 都 刘 颖(武汉市黄陂区第一中学 湖北 武汉 430300)
傅科摆是法国物理学家傅科1851年在巴黎首先制成,摆线长大约是67 m,通过这个实验证明地球在自转.由于科氏力的存在,傅科摆在来回摆动的同时又在绕竖直轴缓慢的转动,类似水星近日点的进动现象.大学教材[1]在分析傅科摆时,认为摆球在竖直方向上没有运动,摆线的拉力近似等于摆球的重力,得到摆球的振动规律,这样处理可以让小球的运动有解析解.若忽略地球的自转,按照以上分析发现傅科摆的运动轨迹可能是椭圆,但实际上小球的运动轨迹不可能是椭圆.
1 傅科摆的动力学微分方程
如图1和图2所示,傅科摆所处纬度为λ,摆线长为R,摆球质量为m,重力加速度为g,则
(1)
摆球的限制方程为
x2(t)+y2(t)+[R-z(t)]2=R2
(2)
式(1)没有解析解,可以这样近似处理
(3)

图1 傅科摆在地球上的坐标系

图2 傅科摆受力分析
式(1)中最后一式变为
(4)
则式(1)前两项可变为

(5)
进一步分析,可得傅科摆的运动规律[1~5],
(6)
式(6)中A,B是两个积分常数,其值由摆球的初始条件决定.
以上处理可等效为:一根原长为零的弹簧(ZLS)振子在匀强磁场中的运动[6],带电粒子所受洛伦兹力与科氏力可以等效[3];若傅科摆在赤道处摆球不受科氏力,傅科摆的运动是球面摆,其运动轨迹不可能是椭圆,其运动轨迹类似水星近日点进动现象[7];参考文献[1]之所以认为傅科摆在赤道处时运动轨迹可能是椭圆,是因为它没有考虑摆球在竖直方向上的运动.
2 傅科摆在地球两极处运动规律
设傅科摆所处纬度为λ,从图3可以看出地球自转的角速度ω0在xOz平面内,并与-x方向的夹角为λ,由图3可知角速度为
ω0=-iω0cosλ+kω0sinλ
(7)
其中ω0的模为一个定值,即为地球自转的角速度.

图3 角速度的方向
对于傅科摆而言,因为地球的自转,摆球所受的科氏力为
F科=-2mω0×v′
(8)
(1)当ω0沿z方向时,vθ对应的F科沿vφ方向,大小为2mvθω0cosθ,vφ对应的F科过z轴,如图4所示,对z轴应用角动量定理有
2mvθω0Rcosθsinθdt=d(mvφRsinθ)
(9)

d(mvφRsinθ+mω0R2cos2θ)=0
(10)
得
mvφRsinθ+mω0R2cos2θ=C
(11)
所以,傅科摆此时正则动量守恒.

图4 傅科摆正则动量研究
(2)若还存在ω0x,则2mvφ×ω0x与z轴平行,对z轴不产生力矩,如图5所示,有
v∥=vθcosθvz=-vθsinθ
(12)

图5 傅科摆的经向速度
由于2mv∥×ω0x与z轴平行,不产生力矩,2mvz×ω0x沿-j方向,它对z轴的冲量矩为
(Rsinθcosφi+Rsinθsinφj)×
(-2mvθω0cosλsinθj)dt=
Mdt=-2Rmω0vθsin2θcosφcosλdt=
-2mR2ω0sin2θcosφcosλdθ
(13)
因为φ也是变量,所以式(13)不能写成全微分的形式,对z轴用角动量定理
-2mR2ω0sin2θcosφcosλdθ=
d(mvφRsinθ+mφ0R2sinλcos2θ)
(14)
参考文献[2]之所以认为“傅科摆在水平面内正则动量守恒”,是因为它没有考虑摆球在竖直方向的振动,故摆球在竖直方向运动引起的科氏力为零;若考虑摆球在竖直方向上运动,则傅科摆只在地球两极处正则动量守恒.
2.1 傅科摆运动的两个速度
如图6所示,在球坐标系中,由机械能守恒和正则动量守恒,有[8]
(15)
mvφRsinθ+mω0R2cos2θ=mω0R2cos2θ0
(16)
联立式(15)、(16)得
图6 傅科摆速度与角度关系
2.2 傅科摆运动的周期

(18)
在一个周期内,沿纬线方向转过的角度Δφ,由于
(19)
所以
(20)
轨迹闭合性的条件
n1Δφ=2πn2
(21)
式中,n1,n2为正整数.
3 傅科摆运动的数值模拟解
傅科摆的实际运动非常复杂,没有解析解,可以进行数值模拟分析和近似分析.
3.1 傅科摆运动的数值模拟图


图8 z与t关系
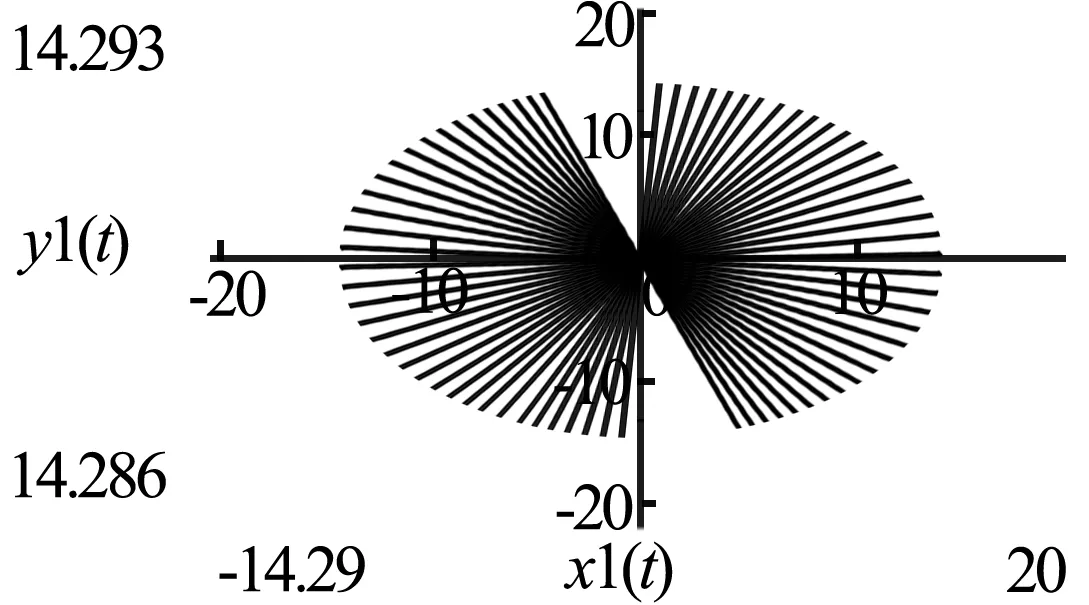
图9 傅科摆进动轨迹1
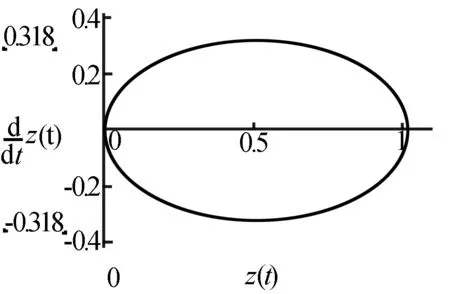
图10 z′与z相图

图11 x′与x相图

图12 y′与y相图


图13 x和y与t关系

图14 z与t关系

图15 傅科摆进动轨迹2
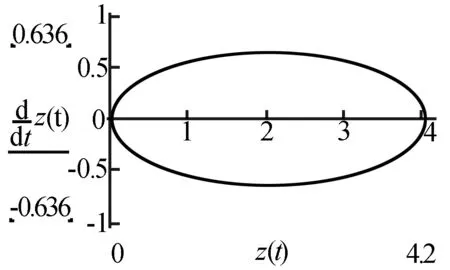
图16 z′与z相图

图17 x′与x相图

图18 y′与y相图

图19 x和y与t关系

图20 z与t关系

图21 傅科摆进动轨迹3

图22 z′与z相图
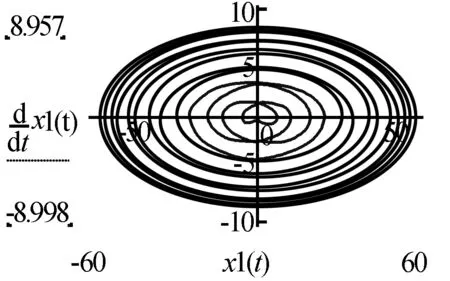
图23 x′与x相图

图24 y′与y相图
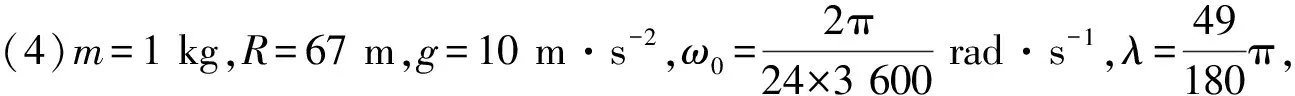

图25 x和y与t关系

图26 z与t关系

图27 傅科摆进动轨迹4
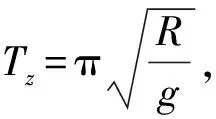
3.2 傅科摆运动的近似解
笔者结合上面的数值模拟解猜想傅科摆在x轴、y轴和z轴方向上运动近似解分别为
(22)

3.3 傅科摆运动近似解与数值模拟解对比
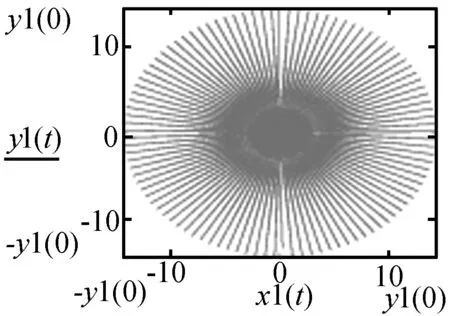
图28 傅科摆进动图
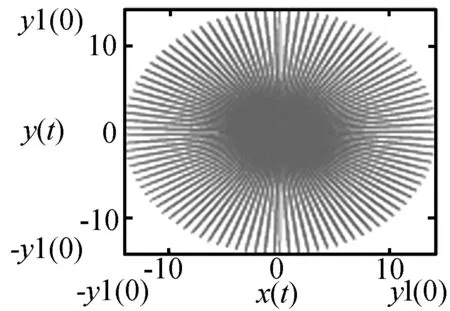
图29 傅科摆进动近似解

图30 摆长近似解的相对误差

图31 近似解能量的相对误差

图32 x近似解与数值模拟解对比图

图33 y近似解与数值模拟解对比图
通过以上6幅图的对比,可以发现傅科摆运动的近似解与数值模拟解的相对误差很小,尤其是x与y的两种解几乎重合,充分说明在误差允许范围内傅科摆运动近似解的合理性.
3.4 傅科摆在赤道处进动现象
若将傅科摆放在赤道处,则其所受科氏力为零.先让摆球在某一水平内做匀速圆周运动,再让小球的角速度有一个微扰,则摆球一种可能运动轨迹的三视图如图34~36所示.

图34 x与y关系图

图35 z与x关系图

图36 z与y关系图
可以发现,摆球的运动轨迹是一种闭合周期解,其在水平面上的投影类似“水星近日点进动”现象;最外侧与最内侧分别对应小球运动的最高点和最低点,两幅侧视图完全相同;若小球在纬线方向和在经线方向上运动周期之比是有理数,则小球在三维空间的运动轨迹有闭合周期解[9];若摆球初始角速度满足特定条件时,其运动轨迹侧视图可能是李萨如图形[7].
4 结束语


