基于本征正交分解的斗轮堆取料机俯仰结构降阶方法

董祥雨，魏代同，李宏坤

大连理工大学机械工程学院 辽宁大连 116024

斗 轮堆取料机是在斗轮挖掘机基础上发展起来 的一种现代化连续散料装卸机械，在一些散料装卸的港口，煤、矿石等料场用于散料的堆存、挖取和均料[1]。其中，悬臂式斗轮堆取料机是应用和发展最早的连续化堆取料装置，具有生产效率高、能耗少、成本低、操作简单及安全可靠等诸多优点。斗轮堆取料机作为效率较高的连续散料装卸机械设备，其性能的好坏决定着整个散货运输作业系统的效率高低[2]。斗轮堆取料机的俯仰结构是其核心钢架结构，其受到的载荷比较复杂，以斗轮堆取料机俯仰结构为研究对象进行静、动力学分析研究，对保证斗轮堆取料机的安全运行和对其结构进行改进设计至关重要[3]。对俯仰结构进行模态特性和动力学特性分析，可以得到其在外界载荷作用下的动力学响应分析结果。这些分析结果不仅可以用来找出其结构设计中的薄弱点以及不合理之处，从而对其进行改善，进而达到提高结构疲劳寿命的目的；还能够根据振动特性分析，在结构设计过程中将其固有频率避开激励源频率，避免在运行时产生共振。

由于大型复杂结构的精细有限元模型包含百万甚至上千万个自由度，其动力学分析效率很低，在求解过程中会产生较大的计算成本[4]；因此，研究大型复杂结构的动力学模型降阶方法具有重要意义。

经过发展，高维复杂系统动力学模型降阶形成了一些比较成熟的降阶方法[5-7]，常用的降阶方法有 3 种：简化模型法、投影法和数据拟合法。本征正交分解 (Proper Orthogonal Decomposition，POD) 是一种有效的数据分析方法，能够得到高维系统的低维近似表达，用于线性和非线性结构的系统分析。由于 POD 方法的有效性和准确性，其不仅能够极大减少系统的自由度，还能够大幅提高计算效率。POD 方法广泛应用在不同领域，例如结构动力学[8-10]、优化设计[11]及流体力学[12]等。靳玉林针对滚动轴承支承的复杂转子系统展开降阶研究，研究表明 POD 方法能够快速精确地获得复杂转子-轴承系统低阶主共振转速范围内的振动特性[13]；路宽基于瞬态响应采用 POD 方法对不同的松动故障模型的动力学特性进行了研究，验证了瞬态 POD 方法得到的简化模型能够很好地保留原始系统的动力学特性，以及瞬态 POD 方法的有效性和准确性[14]；Segala 等人利用 POD 方法对非线性支撑的简支梁进行了模型降阶，验证了通过较少的模态数量能够获得原系统的主要动力学特性，在一定参数范围内具有较好的鲁棒性[15]。

笔者针对堆取料机俯仰结构，提出了采用 POD 的模型降阶方法，构建了俯仰结构的降阶模型，并通过与全阶有限元模型动力学特性的对比分析，验证了降阶方法的有效性。

1 基于 POD 的模型降阶方法

POD 方法主要是在全阶系统计算结果或试验数据的基础上，建立一组能够充分描述全阶系统动力学特性的正交基来描述系统的主要特性。本征正交分解方法又称 Karhunen-Loève 分解、主成分分析 (Principal Component Analysis，PCA)、奇异值分解 (Singular Value Decomposition，SVD)、Hotelling 变换[16]。POD 方法本质上是一种统计方法，POD 降阶模态或降阶基函数是通过求解自相关矩阵的特征向量获得，而自相关矩阵是具有统计意义的 2 阶中心矩。POD 方法的基本思想是：通过复杂系统的数值仿真信号或试验数据信号构造自相关矩阵，再求解自相关矩阵的特征向量，获得 POD 降阶模态或降阶基函数，然后将高维系统投影到前几个最大特征值对应的降阶模态张成的子空间上，从而达到降阶的目的。

1.1 快照矩阵的建立

选取计算不同时刻下全阶系统的节点位移响应数据后，存储在快照矩阵Y中。快照矩阵

其中Y∈Rm×n，式中：m为全阶系统的自由度数量；n为快照数据的数量；y(ti) 为不同时刻下系统的位移响应。

1.2 POD 基底的获取

POD 方法的本质是在全阶系统的计算结果或试验数据的基础上，建立一组能够充分描述全阶系统动力学特性的正交基，使得全阶系统向正交基投影后误差最小。标准正交基

则 POD 投影应满足[17]

式中：φj为 POD 模态正交基；矩阵Φ为 POD 模态正交基的组合。

式 (3) 的最小值问题等价为原全阶系统在 POD 基上的投影最大，即

引入拉格朗日乘子λ，可以将上述最值问题转化为优化问题：

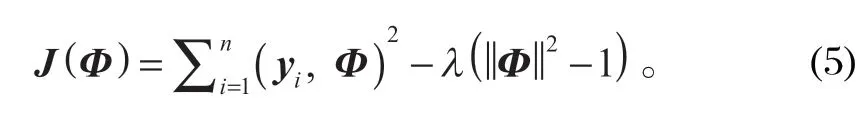
式 (5) 中的优化问题又等价于

即最终转化为求特征值问题。

定义相关矩阵

通过奇异值分解的方法计算求解相关矩阵R的特征值和特征向量，并按特征值从大到小的顺序进行排列，得到相关矩阵R的一组特征值λ={λ1，λ2，…，λm}，及其对应的特征向量φi(i=1，2，…，n)。

第i个 POD 模态基向量可表示为

利用得到的 POD 模态基向量，任意时间和空间的位移响应可以表示为 POD 模态基向量线性组合，即

式中：ui(t) 为 POD 模态坐标。

POD 模态基向量具有特征值快速下降的特点，前几个正交基向量能够表征系统的大部分特征。降阶维数通过定义奇异值或自相关矩阵特征值 (降阶模态) 的能量百分比来确定[16]。一般情况下，为了尽可能少地选取 POD 模态基向量，通过降阶空间的总能量与全阶空间的总能量之比ε进行 POD 模态基向量的截取，ε可以表征为

通常要求ε≥95%，有的要求ε≥99%。按照能量占比原则截取之后的 POD 模态基向量，可以将全阶系统投影到低维的降阶子空间，从而实现系统的降阶。截取之后的 POD 模态基向量Φ∈Rk×k，k＜＜n，降阶后的系统位移响应可以表示为

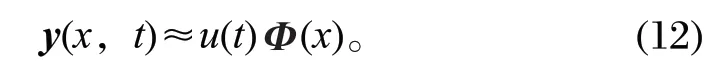
1.3 降阶模型分析

一般大型复杂系统的全阶动力学方程为

式中：M、C、K分别为全阶模型的整体质量矩阵、阻尼矩阵和刚度矩阵；、、y分别为外载荷F作用下全阶系统的加速度响应向量、速度响应向量和位移响应向量。

将降阶后的系统位移响应式 (12) 代入全阶系统的动力学方程 (13) 中，原动力学方程可表示为

与全阶系统相比，系统自由度由n降为k，系统的动力学方程的维数大大降低，由此可得一个低维的动力学模型。求解降阶模型的方程组式 (14)，求解完式中：成后将计算结果映射回全阶空间，可得到全阶系统的最终位移响应。

2 基于降阶模型的俯仰结构动力学响应分析

2.1 斗轮堆取料机的主要工作过程及原理

斗轮堆取料机具有取料和堆料两种功能，这两种功能均通过专门配备的带式输送机来实现，堆料或取料与输送能够同时连续无间断作业，因此具有较高的生产效率。堆取料机在进行取料作业时，悬臂架绕回转中心做往复回转运动，同时斗轮转动挖取物料，靠自重使物料卸到绕回转中心做往复运动的悬臂架带式输送机上。悬臂架每完成一次回转动作，主机构前进一个吃料厚度，然后悬臂架反向回转，完成下一次取料过程。在堆料作业过程中，料场带式输送机运来的物料通过尾车前端漏斗卸至悬臂架带式输送机上，然后输送到斗轮头部抛卸至料场[18]。

2.2 俯仰结构有限元模型构建

以某工程悬臂轨道式 DQ4200.3000.60 型堆取料机的俯仰结构为研究对象，进行几何简化之后的模型如图 1 所示。俯仰结构材料属性参数如表 1 所列。斗轮堆取料机主要技术参数如表 2 所列。

图1 俯仰结构模型Fig.1 Model of pitching mechanism

表1 俯仰结构材料属性参数Tab.1 Material property parameters of pitching mechanism

斗轮堆取料机在工作时所受的外界激励源频率f为斗轮周期性转动取料的冲击频率，

式中：n为斗轮转速，r/min；z为斗轮的铲斗数量，个。

代入表 2 中相应数据，计算得出f=1.2 Hz。

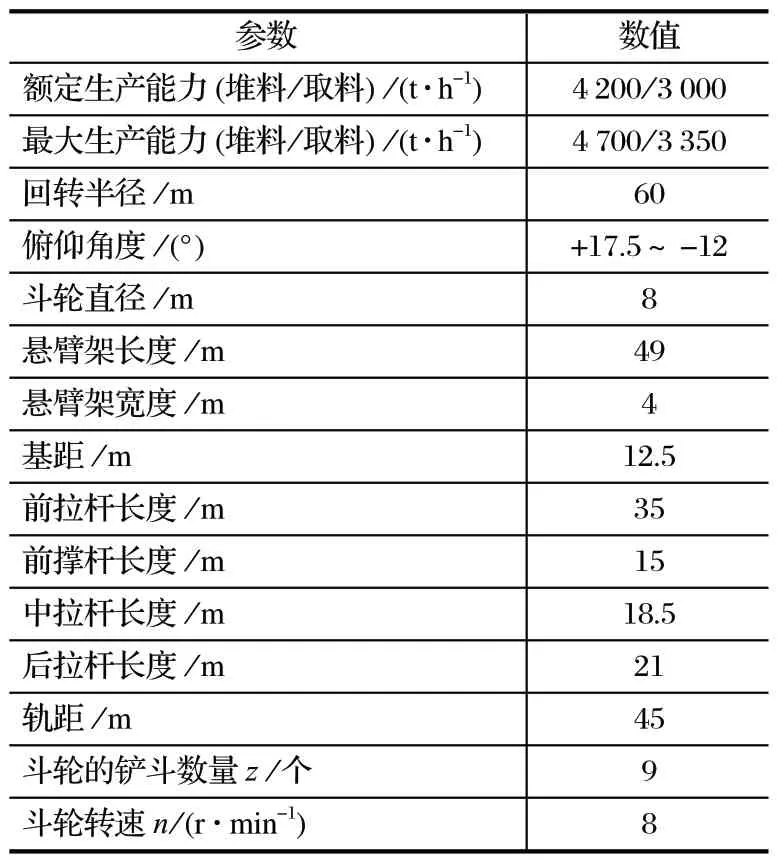
表2 斗轮堆取料机主要技术参数Tab.2 Main technical parameters of bucket-wheel stacker-reclaimer

以往在对于大型复杂结构的有限元分析过程中，单元类型常采用梁单元，可以节省计算资源，但对于需要关注某些特定危险位置的复杂结构，梁单元存在局部响应不精确等问题，只能关注结构整体的状态；而采用实体单元则有足够的响应精度，并且有利于提高降阶模型精度。在 ANSYS 中建立俯仰结构的有限元模型，如图 2 所示。单元类型为 Solid45，每个节点有 3 个自由度，分别为x、y、z方向的移动自由度。模型共有 64 182 个单元、25 462 个节点和 76 386 个自由度。

图2 俯仰结构有限元模型及测点位置Fig.2 Finite element model of pitching mechanism and location of testing points

为了建立斗轮堆取料机俯仰结构动力学分析的降阶模型，笔者采用数值模拟的方法构建快照数据。考虑到斗轮堆取料机俯仰结构的实际工作情况，在斗轮铲斗相应节点上施加激励频率f=1.2 Hz 的简谐载荷，对该俯仰结构的有限元模型进行瞬态动力学分析。设置时间步长 0.005 s，通过有限元方法计算俯仰结构在正常工况边界条件下各节点的位移响应情况，并提取稳定响应阶段 600 个时刻点的快照数据构成快照矩阵。有限元分析计算所用设备配置为 Intel(R) Core(TM) i9-10900K 处理器，主频 3.7 GHz，内存 64 G，64 位操作系统。

2.3 俯仰结构降阶模型的获取

基于全阶模型求解过程中所提取的快照矩阵，根据 POD 的基本原理进行快照矩阵分解，获取 POD 基模态，前 22 阶 POD 模态的特征值如图 3 所示。根据能量占比公式 (11) 进行 POD 模态的截取，POD 模态能量占比随 POD 模态阶数的变化曲线如图 4 所示。

图3 前 22 阶 POD 模态对应的特征值 Fig.3 Eigenvalues of preceding 22 orders of POD modes

图4 POD 模态能量占比随 POD 模态阶数的变化曲线Fig.4 Variation curve of POD modal energy ratio with order number of POD modes

从图 4 可以看出，第 1 阶模态能量占比为 87.13%，前 2 阶模态能量占比为 99.64%，前 3 阶模态能量占比为 99.93%。根据能量占比公式 (11)，在保证降阶模型计算精度的前提下，选择前 3 阶 POD 模态作为投影子空间，即。将全阶模型的系统矩阵及载荷向量投影到 POD 基模态所构成的降阶子空间上，即从而实现模型降阶的目的。

2.4 降阶模型精度分析

2.4.1 俯仰结构的模态特性

基于上述过程所获得的降阶模型进行俯仰结构的模态特性分析，分别计算出斗轮堆取料机俯仰结构的固有频率。俯仰结构全阶模型和降阶模型前 10 阶固有频率对比如表 3 所列。前 3 阶模态振型对比如图 5 所示。

图5 俯仰结构全阶模型和降阶模型前 3 阶模态振型对比Fig.5 Comparison of full-order model and reduced-order model of pitching mechanism in modal vibration mode of preceding 3 orders

表3 俯仰结构全阶模型和降阶模型前 10 阶固有频率对比Tab.3 Comparison of full-order model and reduced-order model of pitching mechanism in natural frequency of preceding 10 orders

从表 3 可以看出，俯仰结构全阶模型与降阶模型计算得到的固有频率吻合较好，前 10 阶固有频率最大误差仅为 0.67%，前 3 阶模态振型对比也显示此降阶方法具有较高的计算精度。

此外，俯仰结构全阶模型固有频率的计算时间约为 1 159 s，而降阶模型固有频率的计算时间为 47.72 s，降阶模型的模态特性计算效率提高了 95.88%。

2.4.2 外部激励下俯仰结构的位移响应

为了进一步验证俯仰结构降阶模型的有效性，对俯仰结构进行外部激励下的位移响应分析。考虑到其实际工况，计算出在斗轮铲斗处应施加相应简谐载荷

其中ω=2πf，f=1.2 Hz。

简谐激励载荷波形如图 6 所示。利用降阶模型进行俯仰结构的动力学响应计算，计算完成后再将所得的方程解投影回原始物理空间。分别提取俯仰结构悬臂的前端、中部和后端测点的位移响应值，测点位置如图 2 所示。分别提取各测点的位移响应值，与在相同简谐激励载荷下的全阶模型进行对比，以此来评估降阶模型的计算精度与计算效率。用 ANSYS 全阶模型和 POD 模型降阶法计算的各测点位移响应对比如图 7～ 9 所示。

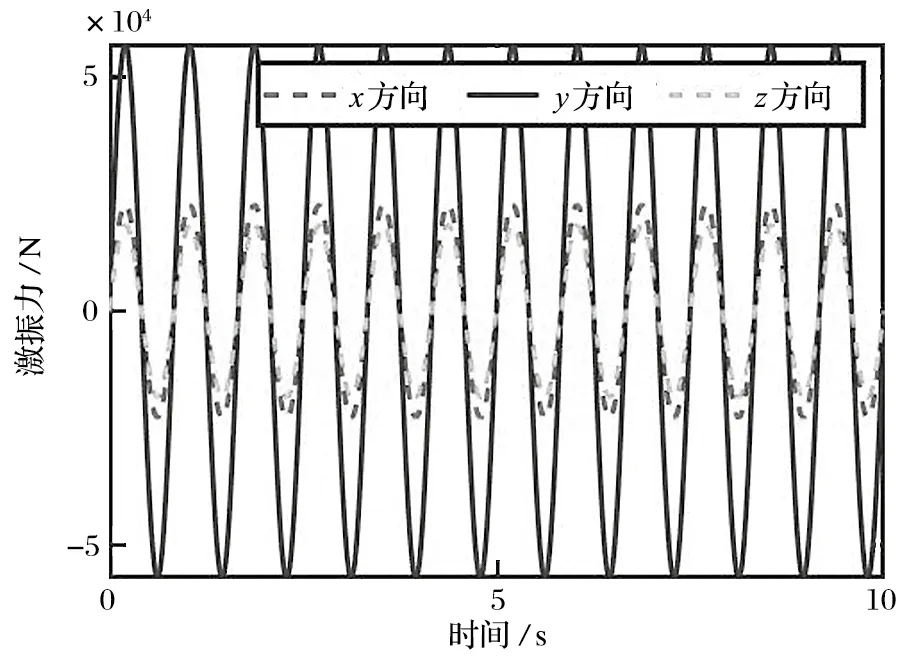
图6 简谐激励载荷波形Fig.6 Waveform of simple harmonic excitation load

从图 7～ 9 可以看出，俯仰结构全阶模型与降阶模型计算得到的位移值吻合较好，可以认为此降阶模型具有较高的计算精度。在分析计算过程中，使用降阶模型求解位移的时间为 46.20 s，远远小于使用全阶模型的计算时间 3 300 s，计算效率提高了 98.6%。

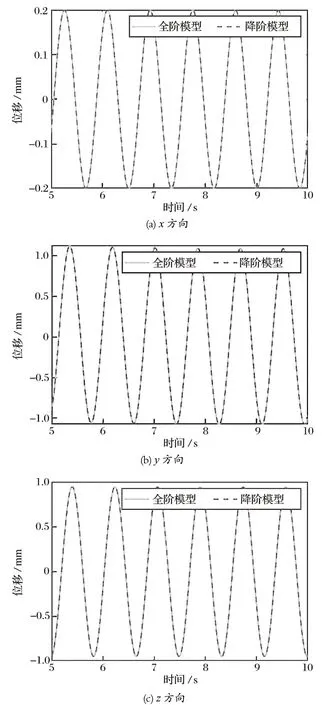
图7 全阶模型和降阶模型 A 测点位移响应对比Fig.7 Comparison of full-order model and reduced-order model in displacement response at testing point A

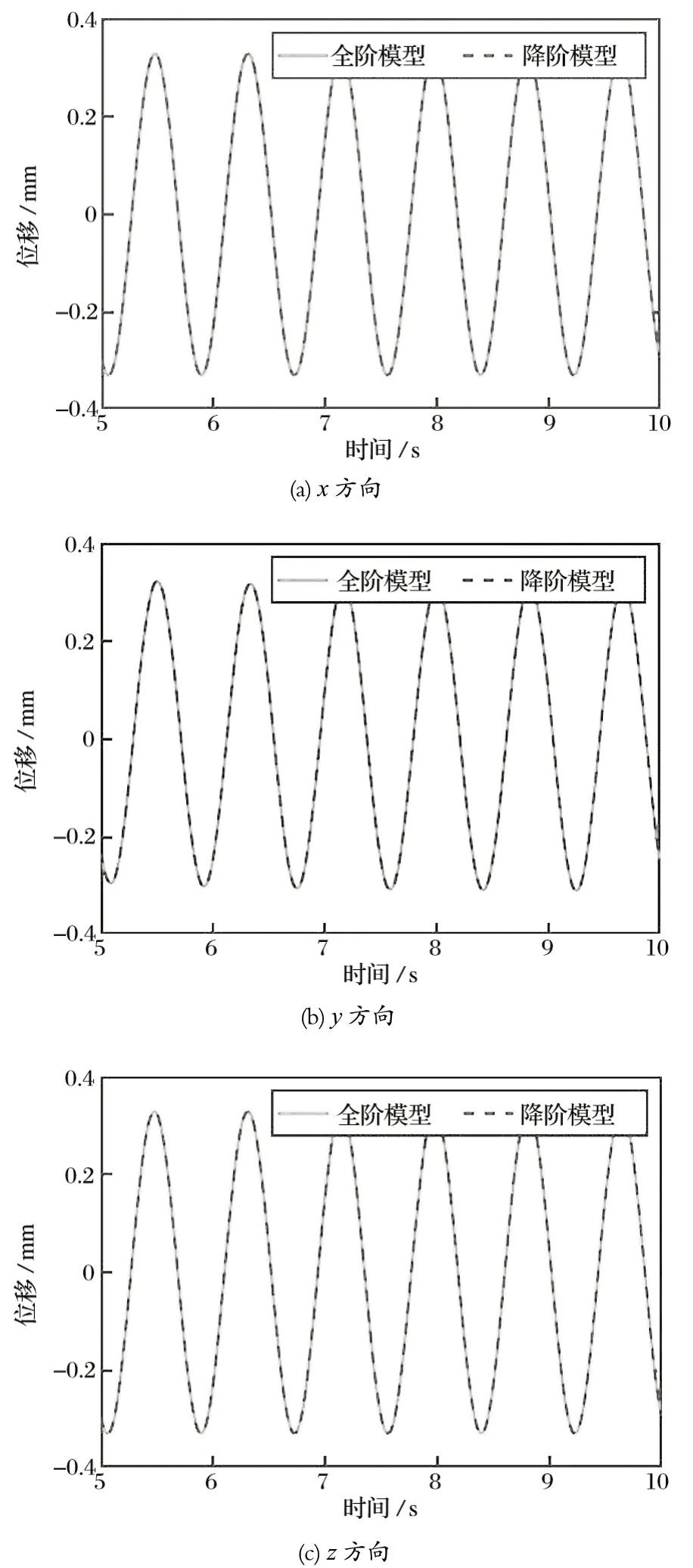
图8 全阶模型和降阶模型 B 测点位移响应对比Fig.8 Comparison of full-order model and reduced-order model in displacement response at testing point B

图9 全阶模型和降阶模型 C 测点位移响应对比Fig.9 Comparison of full-order model and reduced-order model in displacement response at testing point C

3 结论

针对斗轮堆取料机俯仰结构等大型结构动力学分析效率较低的问题，提出了一种基于 POD 的模型降阶方法。首先通过动力学分析获得原模型的位移场并组装成快照矩阵，然后利用 POD 技术提取快照矩阵的主成分作为降阶基，实现模型降阶。结果表明：

(1) POD 方法应用于大型复杂结构的分析预测计算是可行的。虽然快照数据的获取需要花费一定的计算时间，但是在 POD 降阶模型建立完成之后，便能够快捷、准确地得到任意节点的位移响应值，这为大型复杂结构的可靠性评估提供了一种有效可行的方法。

(2) 通过对 POD 降阶模型与全阶模型计算结果进行对比可知，POD 降阶方法能够成功应用于大型复杂结构的动力学计算，并且得到的降阶模型具有较高的精度和效率，在本文中降阶模型固有频率和位移响应的计算效率分别比全阶模型提高了 95.88% 和 98.6%。