函数的极值、最值易错题剖析
■河南省许昌市建安区第一高级中学 蔡慧丽
函数的极值、最值是每年高考中都要考查的知识点,多出现在压轴题的第一问,主要利用函数的单调性来解决此类问题。下面结合实际情况进行总结。
类型一、由极值求参数的范围
例1若f(x)=x(x-c)2在x=1处有极小值,则实数c=______。
解析:f'(x)=3x2-4cx+c2,因为x=1为极小值点,所以f'(1)=3-4c+c2=0,解得c=1或c=3。代入进行检验:当c=1时,f'(x)=3x2-4x+1=(3x-1)(x-1),可得f(x)在和(1,+∞)上单调递增,在上单调递减,所以x=1为极小值点,符合题意;当c=3 时,f'(x)=3x2-12x+9=3(x-1)(x-3),可得f(x)在(-∞,1)和(3,+∞)上单调递增,在(1,3)上单调递减,所以x=1为极大值点,不符合题意。所以c=1。
易错点分析:极小值是在极小值点处的函数值,其中极小值点的验证容易被忽视。
例2设函数f(x)=(x-1)2+blnx,其中b为常数。若函数f(x)有极值点,求b的取值范围及f(x)的极值点。
解析:函数f(x)的定义域为(0,+∞),f'(x)=2(x-1)+,令f'(x)=0,则2x2-2x+b=0。
因为f(x)有极值点,所以2x2-2x+b=0有正的实数根,设方程的根为x1,x2。
若有两个极值点,则x1x2>0,所以。
若有一个极值点,则x1x2=≤0⇒b≤0。
综上可得,b的取值范围为。
方程2x2-2x+b=0 的两根为x=。
当0<b<时,x1=1-,x2=1+,故f(x)的单调区间为表1。
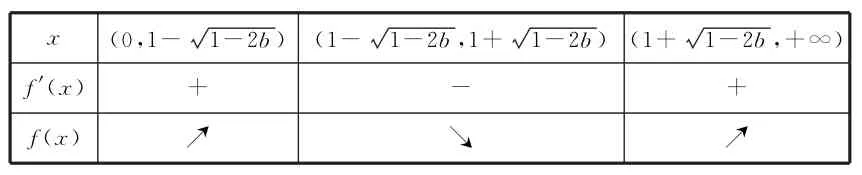
表1
所以f(x)的极大值点为x=1-,极小值点为x=1+。
当b≤0时,x1=1-<0,x2=1+,故f(x)的单调区间为表2。
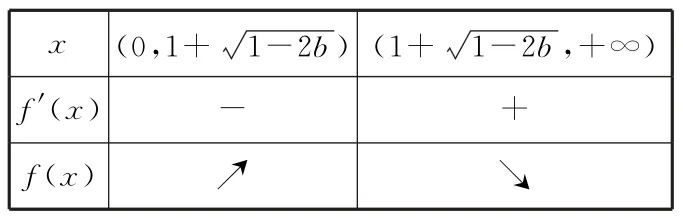
表2
所以f(x)的极小值点为x=1+,无极大值点。
综上可得,当0<b<时,f(x)的极大值点为x=1-,极小值点为x=1+;当b≤0 时,f(x)的极小值点为x=1+,无极大值点。
例3已知函数f(x)=。
(1)讨论函数f(x)的极值点;
(2)若函数f(x)的极大值大于1,求a的取值范围。
解析:f'(x)=(x-a)lnx+-ax+。

易错点分析:极值点为一个实数,不是函数值,要明确是极大值点还是极小值点。
类型二、函数最值问题
例4已知函数f(x)=ax2-ln(x+1)。
(1)若f(x)是(-1,+∞)上的减函数,求实数a的取值范围;
(2)当0<a≤时,求函数f(x)在上的最小值。
解析:(1)f'(x)=2ax-。
令g(x)=2ax2+2ax-1,因为f(x)是(-1,+∞)上的减函数,所以g(x)≤0 在(-1,+∞)上恒成立。
当a=0时,g(x)=-1<0;
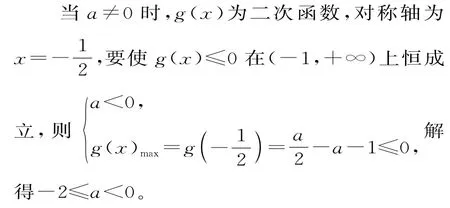
综上可得,实数a的取值范围为[-2,0]。
(2)由(1)知g(x)=2ax2+2ax-1,因为a>0,所以Δ=4a2+8a>0。
由g(x)=0,得x1=,x2=。
因为a>0,所以x1<-1,所以函数g(x)有唯一零点x2。
当x∈(-1,x2)时,g(x)<0,即f'(x)<0,f(x)单调递减;当x∈(x2,+∞)时,g(x)>0,即f'(x)>0,f(x)单调递增。

易错点分析:求函数在无穷区间(或开区间)上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图像,然后借助图像观察得到函数的最值。
极值和最值既是重点又是难点,在复习的过程中,我们要尽可能地规范答题,提高有效得分,力争在2022年高考中取得优异成绩。

